POJ-1422 Air Raid---二分图匹配&最小路径覆盖

题目链接：

https://vjudge.net/problem/POJ-1422

题目大意：

有n个点和m条有向边，现在要在点上放一些伞兵，然后伞兵沿着图走，直到不能走为止
每条边只能是一个伞兵走过，问最少放多少个伞兵

解题思路：

最小路径覆盖

最小路径覆盖=|G|-最大匹配数

重点是，建图的时候，把每个点分成两部分A1，A2，如果有边A->B,就在二分图上加A1->B2

这里的巧妙可以看下面的例子

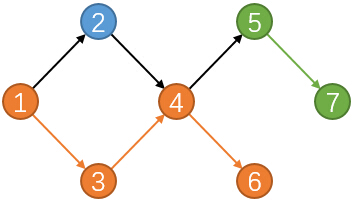
对于一条路径，起点的入度为0，终点的出度为0，中间节点的出入度都为1。

每一个点最多只能有1个后继，同时每一个点最多只能有1个前驱。

假如我们选择了一条边(u,v)，也就等价于把前驱u和后继v匹配上了。这样前驱u和后继v就不能和其他节点匹配。

利用这个我们可以这样来构图：

将每一个点拆分成2个，分别表示它作为前驱节点和后继节点。将所有的前驱节点作为A部，所有后继节点作为B部。

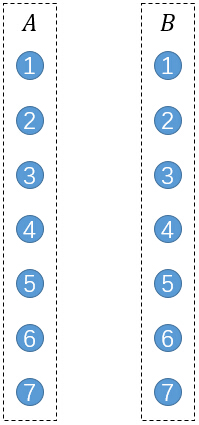
接下来进行连边，若原图中存在一条边(u,v)，则连接A部的u和B部的v。

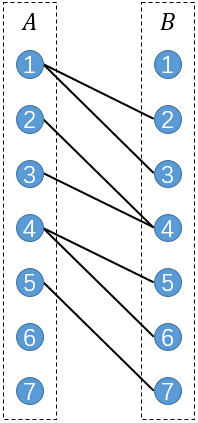
在这个上面做一个最大二分匹配：

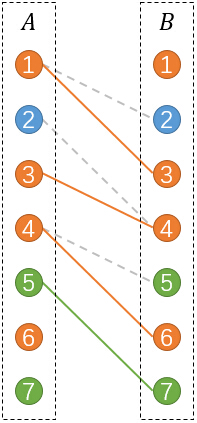
其中实线表示被选中的匹配，虚线表示未被选中的。

有没有发现，和原图刚好有着对应的关系。

这样在匹配结束的时候，我们就可以直接通过匹配的情况来确定选中的路径。

但是如何保证这样就能得到最小的路径覆盖呢？

如果一个点是路径起点的话，它在B部的节点一定是没有匹配上的。

经过最大匹配算法后，B部剩下没有被匹配的点一定是最少的，也就对应了最小需要的路径数。

所以最小路径覆盖的结果才是N-最大匹配数。

（上述例子转载自：https://blog.csdn.net/tramp_1/article/details/52742572）

 #include<iostream>
 #include<cstring>
 #include<cstdio>
 #include<algorithm>
 #include<vector>
 #include<queue>
 using namespace std;
 typedef pair<int, int> Pair ;
 typedef long long ll;
 const int INF = 0x3f3f3f3f;
 const int maxn =  + ;
 int T, n, m, cases;
 vector<int>G[maxn];
 int cx[maxn], cy[maxn];
 bool vis[maxn];
 bool dfs(int u)
 {
     for(int i = ; i < G[u].size(); i++)
     {
         int v = G[u][i];
         if(!vis[v])
         {
             vis[v]  =;//加入增广路
             if(cy[v] == - || dfs(cy[v]))
             {
                 cx[u] = v;
                 cy[v] = u;
                 return ;
             }
         }
     }
     return ;
 }
 int maxmatch()
 {
     int ans = ;
     memset(cx, -, sizeof(cx));
     memset(cy, -, sizeof(cy));
     for(int i = ; i <= n; i++)
     {
         if(cx[i] == -)
         {
             memset(vis, , sizeof(vis));
             ans += dfs(i);
         }
     }
     return ans;
 }
 int main()
 {
     cin >> T;
     while(T--)
     {
         scanf("%d%d", &n, &m);
         int x, y;
         for(int i = ; i <= n; i++)G[i].clear();
         for(int i = ; i <= m; i++)
         {
             scanf("%d%d", &x, &y);
             G[x].push_back(y);
         }
         cout<<(n - maxmatch())<<endl;
     }
     return ;
 }