[URAL1519] Formula 1 [插头dp入门]

题面：

传送门

思路：

插头dp基础教程

先理解一下题意：实际上就是要你求这个棋盘中的哈密顿回路个数，障碍不能走

看到这个数据范围，还有回路处理，就想到使用插头dp来做了

观察一下发现，这道题因为都是回路，所以联通块上方的插头一定两两配对，可以使用括号序列代替最小表示法

分情况讨论一下

情况一：当前格子上方和左方都没有插头

这种时候可以继续，也可以给当前格子加一个下插头一个右插头，相当于一个新的联通分量

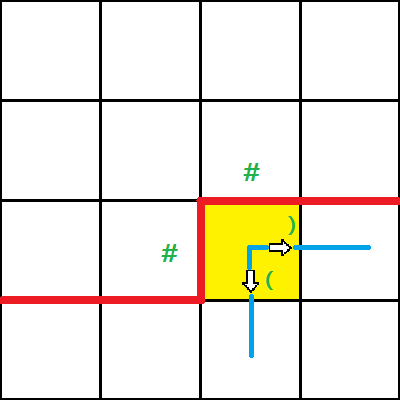
情况二：上方有一个下插头，左边没有

这时有两个决策：可以向右转，也可以继续向下，操作就是分别给这个格子一个右插头或者一个下插头

注意此时新插头的括号类型和原来的那个插头相同（画个图可以理解一下）

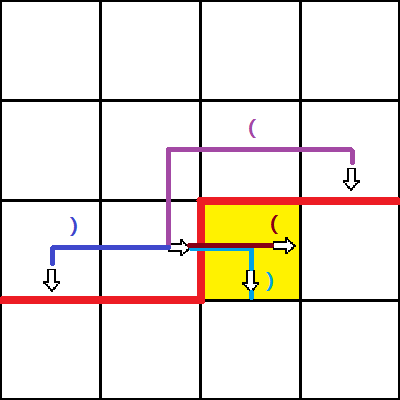
情况三：左边有一个右插头，上面没有

同情况二，转弯或者直走

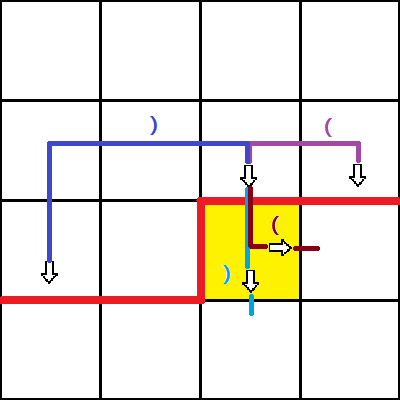
情况四：都有插头，而且两个插头是同一括号

这种情况，我们可以将这两个插头合并，在当前格子把这条路径封闭了

但是这里需要考虑一下其他的插头

我们去掉了两个相同的括号，就需要把另外一个括号反过来配对才行

比如当前的括号序列是 ((##()#())##)，加粗的是我们要合并的两个括号，那么这两个)变成#以后，它们原来匹配的左括号(就失配了，需要其中一个（右边的那个）左括号变成右括号，两个重新配对

也就是((##()#())##)变成((##()#(####)变成((##()#)####)

当然也可以画个图理解一下，两条路径相当于是绕了圈接起来了

这个操作需要扫一遍整个序列，是$O\left(n\right)$的，当然也可以预处理变成$O\left(1\right)$

情况五：都有插头，且两个是)(

这时候直接合并就好了，图片同上（理解一下，博主懒得再画一个图了.......）

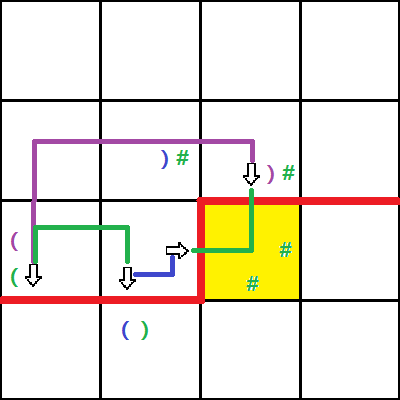
情况六：都有插头，而且两个是()

这种时候只有在最后一个非障碍格子才能合并，标志着路径完全封闭，得到了一个答案

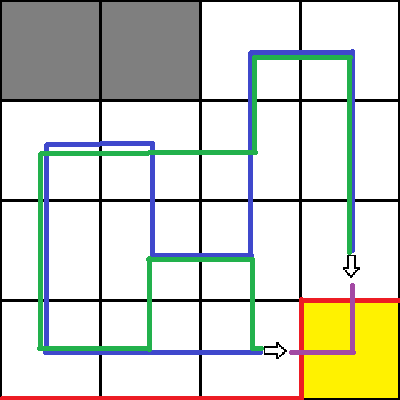
图中的蓝色和绿色代表样例中的两条路径，再最后一个格子合并

状态数略多，可以滚动数组+哈希处理

分类讨论的时候注意可不可以这么做（需要判断下一个格子是否为障碍）

Code：

 #include<iostream>
 #include<cstdio>
 #include<cstring>
 #include<algorithm>
 #define ll long long
 #define hash ddf
 using namespace std;
 int n,m,x[][],cur,pre,ex,ey;
 int st[][];ll ans[][],re;
 int tot[],bit[],state[],st_tot,hash=;
 struct edge{
     int to,next;
 }a[];
 void insert(int sta,ll val){
 //    cout<<"insert "<<sta<<ends<<val<<endl;
     int p=sta%hash,i;
     for(i=state[p];i;i=a[i].next){
         if(st[cur][a[i].to]==sta){
             ans[cur][a[i].to]+=val;return;
         }
     }
     tot[cur]++;
     a[++st_tot].to=tot[cur];
     a[st_tot].next=state[p];
     state[p]=st_tot;st[cur][tot[cur]]=sta;ans[cur][tot[cur]]=val;
 }
 int main(){
     int i,j,k,l,now,down,right;ll val;char s[];
     scanf("%d%d",&n,&m);
     for(i=;i<=n;i++){
         scanf("%s",s);
         for(j=;j<m;j++)
             if(s[j]=='.')
                 x[i][j+]=,ex=i,ey=j+;
     }
     for(i=;i<;i++) bit[i]=i<<;
     cur=;tot[cur]=;ans[cur][]=;st[cur][]=;
     for(i=;i<=n;i++){
         for(j=;j<=tot[cur];j++) st[cur][j]<<=;
         for(j=;j<=m;j++){
 //            cout<<"begin "<<i<<ends<<j<<endl;
             st_tot=;memset(state,,sizeof(state));
             pre=cur;cur^=;tot[cur]=;
             for(k=;k<=tot[pre];k++){
                 now=st[pre][k];val=ans[pre][k];
                 down=(now>>bit[j-])%;right=(now>>bit[j])%;
 //                cout<<"    from "<<now<<ends<<val<<ends<<down<<ends<<right<<endl;
                 if(!x[i][j]){
                     if(!down&&!right){
                         insert(now,val);continue;
                     }
                 }
                 else if(!down&&!right){
                     if(x[i][j+]&&x[i+][j])
                         insert(now+(<<bit[j-])+((<<bit[j])<<),val);
                 }
                 else if(!down&&right){
                     if(x[i][j+]) insert(now,val);
                     if(x[i+][j])
                         insert(now-right*(<<bit[j])+right*(<<bit[j-]),val);
                 }
                 else if(down&&!right){
                     if(x[i+][j]) insert(now,val);
                     if(x[i][j+])
                         insert(now+down*(<<bit[j])-down*(<<bit[j-]),val);
                 }
                 else if(down==&&right==){
                     int cnt=;
                     for(l=j+;l<=m;l++){
                         if((now>>bit[l])%==) cnt++;
                         if((now>>bit[l])%==) cnt--;
                         if(!cnt){
                             insert(now-(<<bit[l])-(<<bit[j])-(<<bit[j-]),val);
                             break;
                         }
                     }
                 }
                 else if(down==&&right==){
                     int cnt=;
                     for(l=j-;l>=;l--){
                         if((now>>bit[l])%==) cnt++;
                         if((now>>bit[l])%==) cnt--;
                         if(!cnt){
                             insert(now+(<<bit[l])-((<<bit[j])<<)-((<<bit[j-])<<),val);
                             break;
                         }
                     }
                 }
                 else if(down==&&right==){
                     insert(now-((<<bit[j-])<<)-(<<bit[j]),val);
                 }
                 else if(down==&&right==){
                     if(i==ex&&j==ey) re+=val;
                 }
             }
         }
     }
     printf("%lld\n",re);
 }