啊哈算法之宽搜BFS解救小哈

简述

本算法摘选自啊哈磊所著的《啊哈！算法》第四章第三节的题目——BFS算法再次解救小哈。文中代码使用C语言编写，博主通过阅读和理解，重新由Java代码实现了一遍，以此来理解BFS算法。关于解救小哈的迷宫题目，可以参看前一篇博文。

啊哈算法之解救小哈：https://www.cnblogs.com/captainad/p/11039967.html

解法思路

本篇博文，我们将利用广度优先搜索（Breadth First Search, BFS）（也称宽度优先搜索）算法来解决这个问题。

假设有如下迷宫地图：

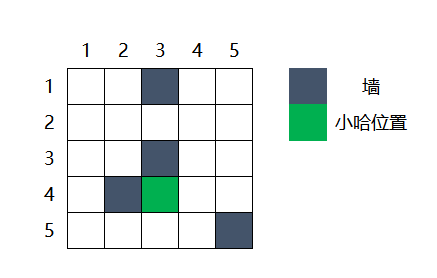
最开始，我们从(1, 1)的位置开始，一步之内能够到达的点有(1, 2)和(2, 1)。

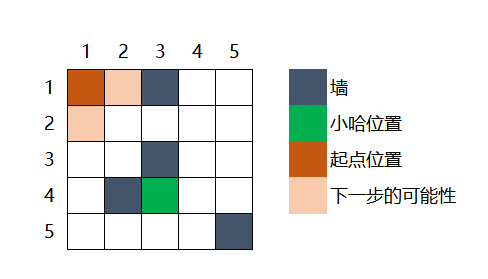
但是小哈并不在这两个点上，那我们只能通过(1,  2)和(2, 1)这两个点继续往下走。比如我们现在走到了(1, 2)这个点，之后又有可能到那个新的点呢？只有(2, 2)了，因为(1, 3)这个点是墙，无法通行的。那再看看通过(2, 1)这个点再走一步能够到达哪些点？可以到达(2, 2)和(3, 1)。此时会发现(2, 2)这个点既可以从(1, 2)到达也可以从(2, 1)到达，并且都只使用了2步。为了防止一个点多次被走到，我们使用桶（book数组）来记录是否被走到过。

此时我们可以走到的点就全部走到了，有(2, 2)和(3, 1)，但是小哈并不在这两个点上，那我们得继续尝试往下找，看看通过(2, 2)和(3, 1)这两个点还能到达哪些新的没有走过的点。通过(2, 2)这个点我们可以到达(2, 3)和(3, 2)，通过(3, 1)这个点我们可以到达(3, 2)和(4, 1)。现在3步可以到达的点有(2, 3)、(3, 2)和(4, 1)，依旧没有到达目标位置即小哈所在的点，那么我们需要重复刚才的方法，直到到达小哈所在的点为止。

总结上面的算法，我们可以用一个队列来模拟这个过程。

我们从一个点开始，并先将这个点入队，开始扩展时，分别往上下左右四个方向走一步，如果这一步没有被走过且没有遇到墙，则将这一步的点位入队，继续扩展，当对上一个点位扩展完了之后，这个点位对于当前来说已经没有用了，就将这个点位出队，接下来，在刚刚那个点位扩展出来的这几个点位的基础上按照上面的方式继续向下探索，这样一来，我们可以记录下从起点开始每走一步就能到达的点位，如果没有到达目标点位，则需要继续探索，否则停止。

我们从上面的图示结合队列来进心一番运算，来明白使用队列解决此问题的奥秘。

首先我们从(1, 1)这个点开始，将这个点入队，然后开始往上下左右四个方向（可使用数组来表示方向）进行探索，发现可以向右到达(1, 2)以及向下到达(2, 1)，并且每扩展到一个可行的点位就入队列，向左和向上就出界了，于是从(1, 1)这个点走一步能够扩张到的点已经全部找齐，此时队列中就有(1, 1)、(1, 2)和(2, 1)，对(1, 1)这个点位扩展完毕之后，这个点就没有存在的意义了，所以将此点出队，于是队首就是(1, 2)，接着我们开始从(1, 2)这个点开始向四个方向探索，重复上面的步骤即可，直到找到目标为位置为止。（可以结合画图来理解这个步骤和意图）

从上面的分析我们可以得出，从某个点开始探索，每次往四个方向探索，且只走一步，遇到可行的点位就入队列，探索完一番之后，将队首的那个点位出队，因为这个点位就探索完了，接着往下一个点位探索，即新队首的点位，如此往复层层递进，直到探索到目标位置。

代码实现

 /**
  * @Project: dailypro
  * @PackageName: com.captainad.algorithm
  * @Author: Captain&D
  * @Websit: https://www.cnblogs.com/captainad/
  * @DateTime: 2019/6/19 15:31.
  * @Description: 使用广度优先搜索算法解救小哈
  */
 public class SaveBfs {

     /**
      * 自定义节点，表示地图上的某个点位及其相关信息
      */
     static class BfsNode {

         /** 横坐标 */
         int x;

         /** 纵坐标 */
         int y;

         /** 父节点在队列中的编号，输出路径时使用 */
         int f;

         /** 步数 */
         int s;
     }

     /**
      * 自定义队列，用来记录探索点位的步骤
      */
     static class BfsQueue {
         BfsNode[] data = new BfsNode[2500];
         int head;
         int tail;
         public BfsQueue(int head, int tail) {
             this.head = head;
             this.tail = tail;
         }
     }

     public static void main(String[] args) {

         // 定义一个表示走方向的数组，分别时向右、向下、向左、向上
         int[][] next = {{0, 1}, {1, 0}, {-1, 0}, {0, -1}};

         // 定义一个桶，用来标记已经路过的点
         int[][] book = new int[50][50];

         // 初始化地图矩形大小，初始化地图数据，略
         int m = 5, n = 4;
         int[][] map = new int[50][50];

         // 测试用数据
         map[0][0] = 0;
         map[0][1] = 0;
         map[0][2] = 1;
         map[0][3] = 0;
         map[1][0] = 0;
         map[1][1] = 0;
         map[1][2] = 0;
         map[1][3] = 0;
         map[2][0] = 0;
         map[2][1] = 0;
         map[2][2] = 1;
         map[2][3] = 0;
         map[3][0] = 0;
         map[3][1] = 1;
         map[3][2] = 0;
         map[3][3] = 0;
         map[4][0] = 0;
         map[4][1] = 0;
         map[4][2] = 0;
         map[4][3] = 1;

         // 初始化入口坐标
         int startx = 0, starty = 0;

         // 目标点位
         int q = 3, p = 2;

         // 队列初始化
         BfsQueue queue = new BfsQueue(0, 0);

         // 往队列插入迷宫的入口坐标，同时在桶中标记
         BfsNode startNode = new BfsNode();
         startNode.x = startx;
         startNode.y = starty;
         startNode.f = 0;
         startNode.s = 0;
         queue.data[queue.tail] = startNode;
         queue.tail++;

         // 用于标记是否达到目的点位，1表示到达
         int flag = 0;

         // 当队列不为空的时候就一直循环
         while(queue.head < queue.tail) {

             // 下一个点的坐标
             int tx, ty;

             // 枚举四个方向
             for(int k = 0; k < 4; k++) {

                 // 计算下一个点的坐标
                 tx = queue.data[queue.head].x + next[k][0];
                 ty = queue.data[queue.head].y + next[k][1];

                 // 判断下一个点是否越界
                 if(tx < 0 || tx >= m || ty < 0 || ty >= n) {
                     continue;
                 }

                 // 判断是否障碍物或者已经路过的点，否则加入到队列中
                 if(map[tx][ty] == 0 && book[tx][ty] == 0) {
                     // 注意：广度优先搜索里每个点只入队一次，和深度搜索不同，这里不需要将book桶清理
                     // 把经过的点进行标记
                     book[tx][ty] = 1;

                     // 插入新的点加到队列中
                     BfsNode newNode = new BfsNode();
                     newNode.x = tx;
                     newNode.y = ty;
                     // 因为当前点是从head处扩展出来的，所以为了记录路径，需要记录上一个点的位置
                     newNode.f = queue.head;
                     // 步数是之前步数+1
                     newNode.s = queue.data[queue.head].s + 1;
                     queue.data[queue.tail] = newNode;
                     queue.tail++;
                 }

                 // 如果目标点位已经到达，则停止扩展，任务结束，退出循环
                 if(tx == q && ty == p) {

                     // 标记为已结束
                     flag = 1;
                     break;
                 }
             }

             // 结束则退出
             if(flag == 1) {
                 break;
             }

             // 当扩展完一个点之后，这个点就没有记录的必要了，进行出队，再对后面的点进行扩展，
             queue.head++;
         }

         // 打印最后一个节点的步数即可，注意tail指针指向的是最后一个有内容的节点的下一个节点的位置
         System.out.println(String.format("解救小哈最少需要%d步。", queue.data[queue.tail - 1].s));

     }

 }

参考资料

1、《啊哈！算法》/ 啊哈磊著. 人民邮电出版社