POJ 2104 K-th Number （区间第k大）

题意：给定一个序列A，接下来又m个询问，每个询问输出A[L,R]中的第K大。（保证第k大存在）

思路：

　　我想拿来练习“可持久化线段树”的，搜到这个比较巧的算法也可以解决这个问题，叫“归并树？。大概的思想就是和线段树一样，只是线段树上的每个非叶子节点是一个区间，等于该节点的两个孩子节点的区间的拼接起来，而每个区间内保持有序的。那么在查找时就找到这两个区间，二分枚举答案然后在询问区间[L,R]判断否排第k。这里二分答案只需要在线段树的根进行就行了，因为根这个区间是有序的。查找时[L,R]可能会是两个区间的拼接的[L,mid]+[mid+1,R]，所以要在两个区间中分别判断val排行老几，然后加起来就是其在[L,R]的真实排行了，这可以用low_bound函数实现。

 //#include <bits/stdc++.h>
 #include <iostream>
 #include <cstdio>
 #include <cstring>
 #include <map>
 #include <vector>
 #include <algorithm>
 #include <iostream>
 #define pii pair<int,int>
 #define INF 0x3f3f3f3f
 #define LL  long long
 using namespace std;
 const int N=;
 int seq[N], tree[][N];

 void build_tree(int L,int R,int depth)
 {
     if(L==R)
     {
         tree[depth][L]=seq[L];
         return;
     }
     int mid=(L+R)>>;
     build_tree(L,mid,depth+);
     build_tree(mid+,R,depth+);

     //归并
     int first=L, second=mid+, cnt=L;
     while( first<=mid && second<=R )
     {
         if(tree[depth+][first]<tree[depth+][second])
             tree[depth][cnt++]=tree[depth+][first++];
         else
             tree[depth][cnt++]=tree[depth+][second++];
     }
     if(first<=mid)  //左边未完
     {
         for(int i=first; i<=mid; i++)
             tree[depth][cnt++]=tree[depth+][i];
     }
     else            //右边未完
     {
         for(int i=second; i<=R; i++)
             tree[depth][cnt++]=tree[depth+][i];
     }
 }

 int query(int ll,int rr,int L,int R,int val,int depth)  //返回val在[L,R]内的排名-1
 {
     if(L==ll && rr==R)
         return lower_bound( &tree[depth][L], &tree[depth][R+], val)
                 -&tree[depth][L];
     int mid=(ll+rr)>>, cnt=;
     if( R<=mid )         cnt+=query(ll,mid, L,R, val,depth+);
     else if( L>mid )     cnt+=query(mid+,rr, L,R, val,depth+);
     else
     {
         cnt+=query(ll,mid, L,mid, val,depth+);
         cnt+=query(mid+,rr, mid+,R, val,depth+);
     }
     return cnt;
 }

 int main()
 {
     freopen("input.txt", "r", stdin);
     int n, m, L, R, k;
     while(~scanf("%d%d",&n,&m))
     {
         for(int i=; i<=n; i++) scanf("%d",&seq[i]);
         build_tree(, n, );

         while(m--)
         {
             scanf("%d%d%d",&L,&R,&k);
             k--;
             int ll=, rr=n;
             while( ll<rr )  //在tree[0]中二分这个数
             {
                 int mid=ll+(rr-ll+)/;
                 int pos=query(,n, L,R, tree[][mid],);
                 if( pos<=k ) ll=mid;    //所查找的数太小了
                 else         rr=mid-;
             }
             printf("%d\n", tree[][ll]);
         }
     }
     return ;
 }

AC代码

　　主席树解法：按照序列的顺序seq[i]，每插入1个点就建1棵树，而每棵树中有且只有seq[1,i]这个序列，而且不是按照seq[1,i]的顺序，而是变成在该树中是有序的。

　　举例：假设有序列seq[4]={1,3,2,4}。

　　插入第seq[1]后的结果：

　　

　　插入第seq[2]后的结果：

　　

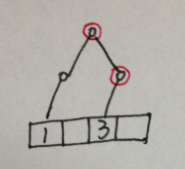
　　插入第seq[3]后的结果：

　　

　　插入第seq[4]后的结果：

　　

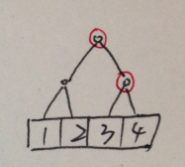
　　观察上面的4张图，红色的点表示是不同于上一幅图的的点，即是新创建的的点。可以看到，每次插入后最多仅有logn个点会被创建。插入是按照有序的方式插入的，比如新插入seq[2]=2，那么其应该排在第二，所以我们需要事先对seq进行排序，才能知道seq[i]的具体应该插在什么位置。

　　得到这些图就可以O(logN)知道第k个数了，比如要在区间[3,4]中找k=1的数字，那么只需要根据root[2]和root[4]就可以算出，只需要在每个节点上用个计数器cnt表示该子树的节点数，具体的话不难算的，自己研究下图吧。

 //#include <bits/stdc++.h>
 #include <iostream>
 #include <cstdio>
 #include <cstring>
 #include <map>
 #include <algorithm>
 #include <vector>
 #include <iostream>
 #define pii pair<int,int>
 #define INF 0x3f3f3f3f
 #define LL  long long
 using namespace std;
 const int N=;
 struct Node
 {
     int L, R, cnt;
 }nod[N*]; //线段树上的节点
 struct Seq
 {
     int val,idx;
     bool operator < ( const Seq &t ) const{return val<t.val;}
 }seq[N];  //序列
 int rank[N], root[N], node_cnt;

 void insert(int rk,int &t,int L,int R)  //每次插入，就建1棵新树
 {
     nod[node_cnt]=nod[t];
     t=node_cnt++;
     nod[t].cnt++;   //此子树的叶子节点数

     if(L==R)    return ;    //到底了。只存此子树的节点数

     int mid=(L+R)>>;
     if(rk<=mid) insert(rk,nod[t].L, L,mid);
     else        insert(rk,nod[t].R, mid+,R);
 }

 int query(int t1,int t2,int k,int L,int R)
 {
     if(L==R)    return R;   //返回的是“有序序列”的下标
     int L1=nod[t1].L, L2=nod[t2].L; //两棵树的左子树节点数量
     int left=nod[L2].cnt-nod[L1].cnt;   //用于判断第k大在左/右
     int mid=(L+R)>>;

     if(k<=left) query(nod[t1].L, nod[t2].L, k, L, mid);           //在左边
     else        query(nod[t1].R, nod[t2].R, k-left, mid+, R );
 }

 int main()
 {
     //freopen("input.txt", "r", stdin);
     int n, m, L, R, k;
     while(~scanf("%d%d",&n,&m))
     {
         node_cnt=;
         memset(root, , sizeof(root));
         for(int i=; i<=n; i++)
         {
             scanf("%d",&seq[i].val);
             seq[i].idx=i;
         }
         sort(seq+,seq+n+);    //需先排序
         for(int i=; i<=n; i++) //反向索引
             rank[ seq[i].idx ]=i;
         for(int i=; i<=n; i++) //按原序逐个插入
         {
             root[i]=root[i-];
             insert(rank[i], root[i], , n);
         }
         while(m--)
         {
             scanf("%d%d%d",&L,&R,&k);
             int idx=query(root[L-], root[R], k, , n); //两树可以同时进行
             printf("%d\n", seq[idx].val);
         }
     }
     return ;
 }

AC代码