算法学习记录-图(DFS BFS)
图：
目录：
1.概念
2.邻接矩阵（结构，深度/广度优先遍历）
3.邻接表（结构，深度/广度优先遍历）
图的基本概念：
数据元素：顶点
1.有穷非空（必须有顶点）
2.顶点之间为边（可空）
无向图：边没有方向，用（vi，vj）表示，（vj，vi）也可。
有向图：边有方向，称为弧，用<vi，vj>表示。vi尾，vj头
简单图：不存在顶点到其自身的边，且同一条边不重复出现。
无向完全图：无向图中，所有的顶点都有边连接。 边的条数：n*（n-1）/2
有向完全图：在有向图中，如果任意两个顶点之间都存在方向互为相反的两条弧。
有很少条边或者弧的图称 稀疏图，反之称为稠密图。
边的相关数称为权。
图的存储
有向图：
入度：就是指向该顶点的边的个数
出度：就是该顶点指向其他顶点的边的个数
存放图的方式：
1.邻接矩阵
2.邻接表
3.十字链表
4.邻接多重表
5.边集数组
遍历：
1.深度优先遍历（DFS）
2.广度优先遍历（BFS）
-------------------------------------------------------------------------------------
================================================
以此无向图作例子：
##################################################################
（1）.邻接矩阵（9个顶点）
##################################################################
我们需要一个顶点数组，一个边数组：
顶点数组 {A,B,C,D,E,F,G,H,I}
边数组：
（其中 $代表无临边，在数组总存放为65535）
a.结构：
#define MAXVEX 100
#define IFY 65535 typedef char VertexType;
typedef int EdgeType; //静态图-邻接矩阵
typedef struct {
VertexType vexs[MAXVEX];
EdgeType Mat[MAXVEX][MAXVEX];
int numVexs,numEdges;
}MGraph;
存储形式：
一个数组存放顶点；一个二维数组存放邻接矩阵。
b.初始化图：
bool checkMat(EdgeType *p,VertexType numvex)
{
int i,j;
for (i=;i<numvex;i++)
{
for(j=i+;j<numvex;j++)
{
//printf("[%d][%d] = %d\t",i,j,*(p + MAXVEX*i + j));
//printf("[%d][%d] = %d\n",j,i,*(p + MAXVEX*j + i));
if (*(p + MAXVEX*i + j) != *(p + MAXVEX*j +i) )
{
printf("ERROR:Mat[%d][%d] or Mat[%d][%d] not equal!\n",i,j,j,i);
return false;
}
}
}
return true;
} void init_Grp(MGraph *g,VertexType *v,EdgeType *p)
{
int i,j;
// init vex num
(*g).numVexs = getVexNum(v); //init vexter
for (i=;i<(*g).numVexs;i++)
{
(*g).vexs[i]=*v;
v++;
} //init Mat
for (i=;i<(*g).numVexs;i++)
{
for (j=;j<(*g).numVexs;j++)
{
(*g).Mat[i][j] = *(p + MAXVEX*i + j);
}
}
if(checkMat(&((*g).Mat[][]),(*g).numVexs) == false)
{
printf("init error!\n");
exit();
}
}
c1：深度优先遍历：
//DFS
void DFS(MGraph G,int num)
{
int j;
g_visited[num]=true;
printf(" %c ",G.vexs[num]); for (j = ;j<G.numVexs;j++)
{ if (!g_visited[j] && G.Mat[num][j] == )
{
//printf("g_vis[%d] = %d",j,g_visited[j]);
//printf("Mat[%d][%d] = %d\n",num,j,G.Mat[num][j]);
DFS(G,j);
}
}
} void grp_DFS(MGraph G)
{
int i;
for (i=;i<G.numVexs;i++) // （1）
{
g_visited[i] = false;
}
for (i=;i<G.numVexs;i++) // （2）
{
if (!g_visited[i])
{
DFS(G,i);
}
}
}
解释：
在grp_DFS()函数中，（1）对每个顶点初始化，记录顶点是否被访问过。
（2）对每个没有被访问过的顶点访问。
在DFS()函数中：
for (j = ;j<G.numVexs;j++)
if (!g_visited[j] && G.Mat[num][j] == )
判断该点是否被访问过而且有边，对每个顶点进行递归调用。
下图：
红色：grp_DFS()中，第一次调用时，访问A。从A开始递归调用。
从A开始，首先设置 g_visited[0] = true；判断edge[0][0](A自己)--> [0][1](B顶点)，递归调用DFS()。（注意这里还没完成，在最后递归调用完成后还会继续判断[0][2]...[0][8]）。
进入B，首先设置g_visited[1] = true；判断edge[1][0](A访问过了) --> [1][1](B自己)-->[1][2]（C顶点），递归调用
。。。
绿色：进入G，首先设置g_visited[1] = true；判断edge[6][0] ...[6][8] (DFS函数中for全部循环完成)，退出 --->退回到F，继续完成F的DFS的for循环 --->
退回到E，继续完成DFS的for，进入到H。如此。。。
---> E ---> D ---> C ---> B ---> I
最后退回到A，完成DFS的for循环。
我们可以发现，连通图只需要调用了grp_DFS() 即可完成全部循环。
深度优先遍历完整代码：
#include "stdafx.h"
#include <stdlib.h> #define MAXVEX 100
#define IFY 65535 typedef char VertexType;
typedef int EdgeType; //静态图-邻接矩阵
typedef struct {
VertexType vexs[MAXVEX];
EdgeType Mat[MAXVEX][MAXVEX];
int numVexs,numEdges;
}MGraph; VertexType g_init_vexs[MAXVEX] = {
'A','B','C','D','E','F','G','H','I'}; EdgeType g_init_edges1[MAXVEX][MAXVEX] = {
{,,IFY,IFY,IFY,,IFY,IFY,}, //'A'
{,,,IFY,IFY,IFY,IFY,IFY,}, //'B'
{IFY,,,,IFY,IFY,IFY,IFY,IFY},//'C'
{IFY,IFY,,,,IFY,IFY,IFY,IFY},//'D'
{IFY,IFY,IFY,,,,,,IFY}, //'E'
{,IFY,IFY,IFY,,,,IFY,IFY}, //'F'
{IFY,IFY,IFY,IFY,,,,IFY,IFY}, //'G'
{IFY,IFY,IFY,IFY,,IFY,IFY,,IFY}, //'H'
{,,IFY,IFY,IFY,IFY,IFY,IFY,}, //'I'
}; bool g_visited[MAXVEX]; //打印数组
void prt_maxtix(EdgeType *p,int vexs)
{
int i,j;
for (i=;i<vexs;i++)
{
printf("\t");
for (j=;j<vexs;j++)
{
if( (*(p + MAXVEX*i + j)) == IFY)
{
printf(" $ ");
}
else
{
printf(" %d ", *(p + MAXVEX*i + j));
}
}
printf("\n");
}
} //check the number of vextex
int getVexNum(VertexType *vexs)
{
VertexType *pos = vexs;
int cnt=;
while(*pos <= 'Z' && *pos >= 'A')
{
cnt++;
pos++;
}
return cnt;
} //DFS
void DFS(MGraph G,int num)
{
int j;
g_visited[num]=true;
printf(" %c ",G.vexs[num]); for (j = ;j<G.numVexs;j++)
{ if (!g_visited[j] && G.Mat[num][j] == )
{
//printf("g_vis[%d] = %d",j,g_visited[j]);
//printf("Mat[%d][%d] = %d\n",num,j,G.Mat[num][j]);
DFS(G,j);
}
}
} void grp_DFS(MGraph G)
{
int i;
for (i=;i<G.numVexs;i++)
{
g_visited[i] = false;
}
for (i=;i<G.numVexs;i++)
{
if (!g_visited[i])
{
//printf("xxx[%d]\n",i);
DFS(G,i);
}
}
} bool checkMat(EdgeType *p,VertexType numvex)
{
int i,j;
for (i=;i<numvex;i++)
{
for(j=i+;j<numvex;j++)
{
//printf("[%d][%d] = %d\t",i,j,*(p + MAXVEX*i + j));
//printf("[%d][%d] = %d\n",j,i,*(p + MAXVEX*j + i));
if (*(p + MAXVEX*i + j) != *(p + MAXVEX*j +i) )
{
printf("ERROR:Mat[%d][%d] or Mat[%d][%d] not equal!\n",i,j,j,i);
return false;
}
}
}
return true;
} void init_Grp(MGraph *g,VertexType *v,EdgeType *p)
{
int i,j;
// init vex num
(*g).numVexs = getVexNum(v); //init vexter
for (i=;i<(*g).numVexs;i++)
{
(*g).vexs[i]=*v;
v++;
} //init Mat
for (i=;i<(*g).numVexs;i++)
{
for (j=;j<(*g).numVexs;j++)
{
(*g).Mat[i][j] = *(p + MAXVEX*i + j);
}
}
if(checkMat(&((*g).Mat[][]),(*g).numVexs) == false)
{
printf("init error!\n");
exit();
}
} int _tmain(int argc, _TCHAR* argv[])
{
MGraph grp; init_Grp(&grp,g_init_vexs,&g_init_edges1[][]); //print the number of Vexters
printf("vex num = %d\n",grp.numVexs); //print the maxtix
prt_maxtix(&grp.Mat[][],grp.numVexs); grp_DFS(grp); getchar();
return ;
}
结果：
--------------------------------------------------------------------------------------------------
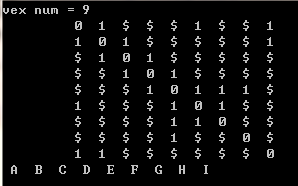
c2：广度优先遍历
void BFS(MGraph G)
{
int i,j;
spQueue que;
init_Queue(&que); for (i=;i<G.numVexs;i++)
{
g_visited[i]=false;
}
for (i=;i<G.numVexs;i++)
{
if (!g_visited[i])
{
g_visited[i]=true;
unshiftQueue(&que,i);
printf(" %c ",G.vexs[i]); while(!isEmptyQueue(que))
{
QueueType crnt = shiftQueue(&que);
for (j=;j<G.numVexs;j++)
{
if (!g_visited[j] && G.Mat[crnt][j] == )
{
g_visited[j]=true;
unshiftQueue(&que,j);
printf(" %c ",G.vexs[j]);
}
}
i=crnt;
} }
}
}
解释：
从一个顶点开始，查看所有和他相连的顶点；从这些相连的顶点中逐次查找与它们相连且没有访问过的点。
这里要借助一个辅助的数据结构---队列。
如下,先将图转化为右边形式。
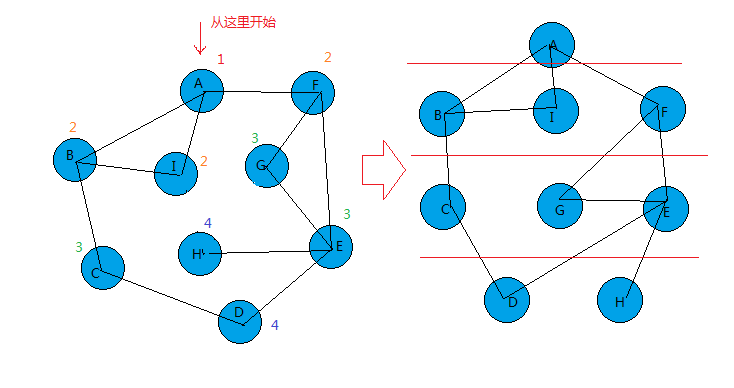
第一层为A，第二层为B I F，第三层为C G E，第四层为 D H。
过程：
a.A开始，A进队。
队列 | A |
b.队列出队一个元素（此时为A），查找与它相连且没有被访问过的元素（B、I、F），使其进队。
队列 A | | --> | B I F | 第一层完成
---
c.重复b过程，直到队列中没有元素为止。 （如果是连通图，则此时全部访问，否则继续查其他顶点，直到所有顶点都遍历。）
队列出列一个元素（此时为B），查找与它相连且没有被访问过的元素（C），使其进队。
队列 B | I F|--> | I F C|
队列出列一个元素（此时为I），。。。 （无）
队列 I | F C | --> | F C |
队列出列一个元素（此时为F），。。。 （G、E），使其进队。
队列 F | C | ---> | C G E | 第二层完成
---
队列 C | G E | ---> | G E D|
队列 G | E D | ---> |E D|
队列 E | D | ---> | D H|
队列 D | H | ---> | H |
队列 H || 完成。。。
完整程序如下：
// grp-mat-bfs-self.cpp : 定义控制台应用程序的入口点。
// #include "stdafx.h"
#include <stdlib.h> #define MAXVEX 100
#define IFY 65535 typedef char VertexType;
typedef int EdgeType; typedef int QueueType; bool g_visited[MAXVEX]; VertexType g_init_vexs[MAXVEX] = {'A','B','C','D','E','F','G','H','I'}; EdgeType g_init_edges[MAXVEX][MAXVEX] = {
{,,IFY,IFY,IFY,,IFY,IFY,}, //'A'
{,,,IFY,IFY,IFY,IFY,IFY,}, //'B'
{IFY,,,,IFY,IFY,IFY,IFY,IFY},//'C'
{IFY,IFY,,,,IFY,IFY,IFY,IFY},//'D'
{IFY,IFY,IFY,,,,,,IFY}, //'E'
{,IFY,IFY,IFY,,,,IFY,IFY}, //'F'
{IFY,IFY,IFY,IFY,,,,IFY,IFY}, //'G'
{IFY,IFY,IFY,IFY,,IFY,IFY,,IFY}, //'H'
{,,IFY,IFY,IFY,IFY,IFY,IFY,}, //'I'
}; //==========================================================================
//静态图-邻接矩阵
typedef struct {
VertexType vexs[MAXVEX];
EdgeType Mat[MAXVEX][MAXVEX];
int numVexs,numEdges;
}MGraph; //==========================================================================
//队列 //队列节点
typedef struct Node {
QueueType data;
struct Node *next;
}QNode,*qQNode; //队列指示
typedef struct {
int length;
qQNode frnt,rear;
}spQueue; void init_Queue(spQueue *Q)
{
(*Q).frnt = NULL;
(*Q).rear = NULL;
(*Q).length = ;
}
bool isEmptyQueue(spQueue Q)
{
if (Q.length == )
{
return true;
}
return false;
}
//进队
void unshiftQueue(spQueue *Q,QueueType elem)
{
//队列空
if (isEmptyQueue(*Q))
{
qQNode n = (qQNode)malloc(sizeof(QNode));
n->data = elem;
n->next = NULL; (*Q).frnt = n;
(*Q).rear = n;
(*Q).length = ;
}
else
{
qQNode n = (qQNode)malloc(sizeof(QNode));
n->data = elem;
n->next = NULL; (*Q).rear->next = n; (*Q).rear = n;
(*Q).length++;
}
} //出队
QueueType shiftQueue(spQueue *Q)
{
if (isEmptyQueue(*Q))
{
printf("Warning:Queue is empty!!!\n");
return NULL;
}
if ((*Q).length == )
{
QueueType sh = (*Q).frnt->data;
(*Q).frnt = NULL;
(*Q).rear = NULL;
(*Q).length = ;
return sh;
}
QueueType sh = (*Q).frnt->data;
(*Q).frnt = (*Q).frnt->next;
(*Q).length--; return sh;
} //打印队列
void prt_que(spQueue que)
{
if (isEmptyQueue(que))
{
return ;
}
qQNode pos = que.frnt;
while(que.rear->next != pos && pos != NULL)
{
printf(" %d ",pos->data);
pos = pos->next;
}
printf("\n");
} //====================================================================
//打印矩阵
void prt_maxtix(EdgeType *p,int vexs)
{
int i,j;
for (i=;i<vexs;i++)
{
printf("\t");
for (j=;j<vexs;j++)
{
if( (*(p + MAXVEX*i + j)) == IFY)
{
printf(" $ ");
}
else
{
printf(" %d ", *(p + MAXVEX*i + j));
}
}
printf("\n");
}
} //check the number of vextex
int getVexNum(VertexType *vexs)
{
VertexType *pos = vexs;
int cnt=;
while(*pos <= 'Z' && *pos >= 'A')
{
cnt++;
pos++;
}
return cnt;
} bool checkMat(EdgeType *p,VertexType numvex)
{
int i,j;
for (i=;i<numvex;i++)
{
for(j=i+;j<numvex;j++)
{
//printf("[%d][%d] = %d\t",i,j,*(p + MAXVEX*i + j));
//printf("[%d][%d] = %d\n",j,i,*(p + MAXVEX*j + i));
if (*(p + MAXVEX*i + j) != *(p + MAXVEX*j +i) )
{
printf("ERROR:Mat[%d][%d] or Mat[%d][%d] not equal!\n",i,j,j,i);
return false;
}
}
}
return true;
} void init_Grp(MGraph *g,VertexType *v,EdgeType *p)
{
int i,j;
// init vex num
(*g).numVexs = getVexNum(v); //init vexter
for (i=;i<(*g).numVexs;i++)
{
(*g).vexs[i]=*v;
v++;
} //init Mat
for (i=;i<(*g).numVexs;i++)
{
for (j=;j<(*g).numVexs;j++)
{
(*g).Mat[i][j] = *(p + MAXVEX*i + j);
}
}
if(checkMat(&((*g).Mat[][]),(*g).numVexs) == false)
{
printf("init error!\n");
exit();
}
} void BFS(MGraph G)
{
int i,j;
spQueue que;
init_Queue(&que); for (i=;i<G.numVexs;i++)
{
g_visited[i]=false;
}
for (i=;i<G.numVexs;i++)
{
if (!g_visited[i])
{
g_visited[i]=true;
unshiftQueue(&que,i);
printf(" %c ",G.vexs[i]); while(!isEmptyQueue(que))
{
QueueType crnt = shiftQueue(&que);
for (j=;j<G.numVexs;j++)
{
if (!g_visited[j] && G.Mat[crnt][j] == )
{
g_visited[j]=true;
unshiftQueue(&que,j);
printf(" %c ",G.vexs[j]);
}
}
i=crnt;
} }
}
} int _tmain(int argc, _TCHAR* argv[])
{
MGraph grp;
init_Grp(&grp,g_init_vexs,&g_init_edges[][]); BFS(grp); getchar();
return ;
}
结果：
=================================================================
##################################################################
（2）.邻接表
##################################################################
如上图：
邻接表如下：
顶点 边
A -> B -> F -> I
B -> A -> C -> I
C -> B -> D
D -> C -> E
E -> D -> F -> G -> H
F -> A -> E -> G
G -> E -> F
H -> E
I -> A -> B
结构：
#define MAXVEX 100
#define IFY 65535 typedef char VertexType;
typedef int EdgeType;
typedef int ArrayIdx; //边节点
typedef struct EdgeNode{
ArrayIdx idx;
struct EdgeNode* next;
}edgeNode;
//顶点节点
typedef struct VexNode{
ArrayIdx idx;
edgeNode *fitstedge;
}vexNode; //图的集合：包含了一个顶点数组
typedef struct {
vexNode adjList[MAXVEX];
int numVextexs,numEdges;
}GraphAdjList;
我通过一个二维字符数组来初始化该图结构：
VertexType g_init_vexs[MAXVEX] = {'A','B','C','D','E','F','G','H','I'};
//====================================
char *g_input[] = {
"A->B->F->I",
"B->A->C->I",
"C->B->D",
"D->C->E",
"E->D->F->G->H",
"F->A->E->G",
"G->E->F",
"H->E",
"I->A->B"
};
初始化函数：
void init_GrapAdjList(GraphAdjList *g,char **str)
{
char **pos = str;
int cnt=;
while (*pos != NULL) //g_input的每行的首指针
{
int i=;
while(**pos != NULL) //g_input的每行字母
{
if(isVexter(**pos)) //判断是否为顶点（我规定‘A’-‘Z’之间为顶点标志）
{
if (i == ) //建立顶点的节点
{
(*g).adjList[cnt].idx = strFindIdx(**pos);
(*g).adjList[cnt].fitstedge = NULL;
i=;
}
else if(i == ) //建立第一个边的节点
{
edgeNode* n = (edgeNode*)malloc(sizeof(edgeNode));
n->idx = strFindIdx(**pos);
n->next = NULL; (*g).adjList[cnt].fitstedge = n;
i=;
}
else //边节点连接到前一个边节点上
{
edgeNode* n = (edgeNode*)malloc(sizeof(edgeNode));
n->idx = strFindIdx(**pos);
n->next = NULL; //first splist
edgeNode *r = (*g).adjList[cnt].fitstedge;
while (r->next != NULL)
{
r = r->next;
}
r->next = n;
}
}
(*pos)++;
}
pos++;
cnt++;
}
(*g).numVextexs = cnt;
}
这样之后，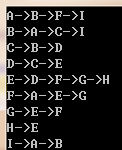
内存中，以其中A为例子：
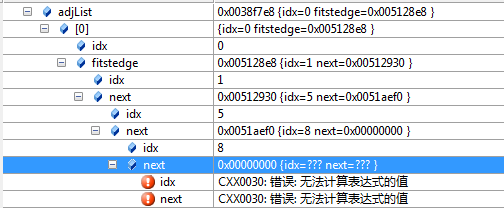
idx 为 索引值 0 ---> 'A'
0(A)---> 1(B) ---> 5(F) ---> 8(I)。
深度优先遍历（邻接矩阵类似）
遍历顺序为：
代码：
void DFS(GraphAdjList GL,int i)
{
edgeNode *p;
g_visited[i]=true;
printf(" %c ",g_init_vexs[GL.adjList[i].idx]); p = GL.adjList[i].fitstedge;
while(p)
{
if (!g_visited[p->idx])
{
DFS(GL,p->idx);
}
p=p->next;
}
} void DFS_Trvs(GraphAdjList GL)
{
int i;
for (i = ;i<GL.numVextexs;i++)
{
g_visited[i] = false;
}
for (i=;i<GL.numVextexs;i++)
{
if (!g_visited[i])
{
DFS(GL,i);
} }
}
结果：
完整代码：
// grp-tab-dfs.cpp : 定义控制台应用程序的入口点。
// #include "stdafx.h"
#include <stdlib.h> #define MAXVEX 100
#define IFY 65535 typedef char VertexType;
typedef int EdgeType;
typedef int ArrayIdx; //边节点
typedef struct EdgeNode{
ArrayIdx idx;
struct EdgeNode* next;
}edgeNode;
//顶点节点
typedef struct VexNode{
ArrayIdx idx;
edgeNode *fitstedge;
}vexNode; //图的集合：包含了一个顶点数组
typedef struct {
vexNode adjList[MAXVEX];
int numVextexs,numEdges;
}GraphAdjList; bool g_visited[MAXVEX]; VertexType g_init_vexs[MAXVEX] = {'A','B','C','D','E','F','G','H','I'};
//====================================
char *g_input[] = {
"A->B->F->I",
"B->A->C->I",
"C->B->D",
"D->C->E",
"E->D->F->G->H",
"F->A->E->G",
"G->E->F",
"H->E",
"I->A->B"
}; ArrayIdx strFindIdx(char ch)
{
int i=;
VertexType *p = g_init_vexs;
while(p != NULL)
{
if(*p == ch)
{
return i;
}
p++;
i++;
}
} VertexType idxFindStr(ArrayIdx i)
{
return g_init_vexs[i];
} void prt_strings(char *p)
{
char *pos = p;
while (NULL != *pos)
{
printf("%c",*pos);
pos++;
}
printf("\n");
} void prt_strArrays(char *p[])
{
char **pos = p;
while( *pos != NULL)
{
prt_strings(*pos);
pos++;
}
} bool isVexter(char p)
{
if (p>='A' && p<='Z')
{
return true;
}
return false;
} void init_GrapAdjList(GraphAdjList *g,char **str)
{
char **pos = str;
int cnt=;
while (*pos != NULL) //g_input的每行的首指针
{
int i=;
while(**pos != NULL) //g_input的每行字母
{
if(isVexter(**pos)) //判断是否为顶点（我规定‘A’-‘Z’之间为顶点标志）
{
if (i == ) //建立顶点的节点
{
(*g).adjList[cnt].idx = strFindIdx(**pos);
(*g).adjList[cnt].fitstedge = NULL;
i=;
}
else if(i == ) //建立第一个边的节点
{
edgeNode* n = (edgeNode*)malloc(sizeof(edgeNode));
n->idx = strFindIdx(**pos);
n->next = NULL; (*g).adjList[cnt].fitstedge = n;
i=;
}
else //边节点连接到前一个边节点上
{
edgeNode* n = (edgeNode*)malloc(sizeof(edgeNode));
n->idx = strFindIdx(**pos);
n->next = NULL; //first splist
edgeNode *r = (*g).adjList[cnt].fitstedge;
while (r->next != NULL)
{
r = r->next;
}
r->next = n;
}
}
(*pos)++;
}
pos++;
cnt++;
}
(*g).numVextexs = cnt;
} void DFS(GraphAdjList GL,int i)
{
edgeNode *p;
g_visited[i]=true;
printf(" %c ",g_init_vexs[GL.adjList[i].idx]); p = GL.adjList[i].fitstedge;
while(p)
{
if (!g_visited[p->idx])
{
DFS(GL,p->idx);
}
p=p->next;
}
} void DFS_Trvs(GraphAdjList GL)
{
int i;
for (i = ;i<GL.numVextexs;i++)
{
g_visited[i] = false;
}
for (i=;i<GL.numVextexs;i++)
{
if (!g_visited[i])
{
DFS(GL,i);
} }
} int _tmain(int argc, _TCHAR* argv[])
{
GraphAdjList grp;
prt_strArrays(g_input);
init_GrapAdjList(&grp,g_input); DFS_Trvs(grp); getchar();
return ;
}
广度优先遍历：
与邻接矩阵类似。
void BFS(GraphAdjList GL)
{
int i,j;
spQueue Q;
init_Queue(&Q); for (i = ;i < GL.numVextexs;i++)
{
g_visited[i] = false;
}
for (i=;i<GL.numVextexs;i++)
{
if(!g_visited[i])
{
g_visited[i] = true;
printf(" %c ",g_init_vexs[i]);
unshiftQueue(&Q,i); while(!isEmptyQueue(Q))
{
i = shiftQueue(&Q);
edgeNode *p = GL.adjList[i].fitstedge;
while(p != NULL)
{
if (!g_visited[p->idx])
{
g_visited[p->idx]=true;
printf(" %c ",g_init_vexs[p->idx]);
unshiftQueue(&Q,p->idx);
}
p=p->next;
}
}
}
}
}
结构，初始化与广度一样。
多了一个辅助结构-队列。与邻接矩阵中队列一样。
结果：
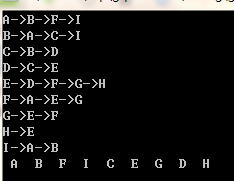
完整函数：
// grp-tab-bfs.cpp : 定义控制台应用程序的入口点。
// #include "stdafx.h"
#include <stdlib.h> #define MAXVEX 100
#define IFY 65535 typedef char VertexType;
typedef int EdgeType;
typedef int ArrayIdx; //边节点
typedef struct EdgeNode{
ArrayIdx idx;
struct EdgeNode* next;
}edgeNode;
//顶点节点
typedef struct VexNode{
ArrayIdx idx;
edgeNode *fitstedge;
}vexNode; //图的集合：包含了一个顶点数组
typedef struct {
vexNode adjList[MAXVEX];
int numVextexs,numEdges;
}GraphAdjList; typedef int QueueType; bool g_visited[MAXVEX]; VertexType g_init_vexs[MAXVEX] = {'A','B','C','D','E','F','G','H','I'};
char *g_input[] = {
"A->B->F->I",
"B->A->C->I",
"C->B->D",
"D->C->E",
"E->D->F->G->H",
"F->A->E->G",
"G->E->F",
"H->E",
"I->A->B"
}; //==========================================================================
//队列 //队列节点
typedef struct Node {
QueueType data;
struct Node *next;
}QNode,*qQNode; //队列指示
typedef struct {
int length;
qQNode frnt,rear;
}spQueue; void init_Queue(spQueue *Q)
{
(*Q).frnt = NULL;
(*Q).rear = NULL;
(*Q).length = ;
}
bool isEmptyQueue(spQueue Q)
{
if (Q.length == )
{
return true;
}
return false;
}
//进队
void unshiftQueue(spQueue *Q,QueueType elem)
{
//队列空
if (isEmptyQueue(*Q))
{
qQNode n = (qQNode)malloc(sizeof(QNode));
n->data = elem;
n->next = NULL; (*Q).frnt = n;
(*Q).rear = n;
(*Q).length = ;
}
else
{
qQNode n = (qQNode)malloc(sizeof(QNode));
n->data = elem;
n->next = NULL; (*Q).rear->next = n; (*Q).rear = n;
(*Q).length++;
}
} //出队
QueueType shiftQueue(spQueue *Q)
{
if (isEmptyQueue(*Q))
{
printf("Warning:Queue is empty!!!\n");
return NULL;
}
if ((*Q).length == )
{
QueueType sh = (*Q).frnt->data;
(*Q).frnt = NULL;
(*Q).rear = NULL;
(*Q).length = ;
return sh;
}
QueueType sh = (*Q).frnt->data;
(*Q).frnt = (*Q).frnt->next;
(*Q).length--; return sh;
} //打印队列
void prt_que(spQueue que)
{
if (isEmptyQueue(que))
{
return ;
}
qQNode pos = que.frnt;
while(que.rear->next != pos && pos != NULL)
{
printf(" %d ",pos->data);
pos = pos->next;
}
printf("\n");
}
//=============================================================== ArrayIdx strFindIdx(char ch)
{
int i=;
VertexType *p = g_init_vexs;
while(p != NULL)
{
if(*p == ch)
{
return i;
}
p++;
i++;
}
} VertexType idxFindStr(ArrayIdx i)
{
return g_init_vexs[i];
} void prt_strings(char *p)
{
char *pos = p;
while (NULL != *pos)
{
printf("%c",*pos);
pos++;
}
printf("\n");
} void prt_strArrays(char *p[])
{
char **pos = p;
while( *pos != NULL)
{
prt_strings(*pos);
pos++;
}
} bool isVexter(char p)
{
if (p>='A' && p<='Z')
{
return true;
}
return false;
} void init_GrapAdjList(GraphAdjList *g,char **str)
{
char **pos = str;
int cnt=;
while (*pos != NULL) //g_input的每行的首指针
{
int i=;
while(**pos != NULL) //g_input的每行字母
{
if(isVexter(**pos)) //判断是否为顶点（我规定‘A’-‘Z’之间为顶点标志）
{
if (i == ) //建立顶点的节点
{
(*g).adjList[cnt].idx = strFindIdx(**pos);
(*g).adjList[cnt].fitstedge = NULL;
i=;
}
else if(i == ) //建立第一个边的节点
{
edgeNode* n = (edgeNode*)malloc(sizeof(edgeNode));
n->idx = strFindIdx(**pos);
n->next = NULL; (*g).adjList[cnt].fitstedge = n;
i=;
}
else //边节点连接到前一个边节点上
{
edgeNode* n = (edgeNode*)malloc(sizeof(edgeNode));
n->idx = strFindIdx(**pos);
n->next = NULL; //first splist
edgeNode *r = (*g).adjList[cnt].fitstedge;
while (r->next != NULL)
{
r = r->next;
}
r->next = n;
}
}
(*pos)++;
}
pos++;
cnt++;
}
(*g).numVextexs = cnt;
} void BFS(GraphAdjList GL)
{
int i,j;
spQueue Q;
init_Queue(&Q); for (i = ;i < GL.numVextexs;i++)
{
g_visited[i] = false;
}
for (i=;i<GL.numVextexs;i++)
{
if(!g_visited[i])
{
g_visited[i] = true;
printf(" %c ",g_init_vexs[i]);
unshiftQueue(&Q,i); while(!isEmptyQueue(Q))
{
i = shiftQueue(&Q);
edgeNode *p = GL.adjList[i].fitstedge;
while(p != NULL)
{
if (!g_visited[p->idx])
{
g_visited[p->idx]=true;
printf(" %c ",g_init_vexs[p->idx]);
unshiftQueue(&Q,p->idx);
}
p=p->next;
}
}
}
}
} int _tmain(int argc, _TCHAR* argv[])
{
GraphAdjList grp;
prt_strArrays(g_input);
init_GrapAdjList(&grp,g_input);
BFS(grp);
getchar();
return ;
}
这两种是常用的图的遍历算法。时间复杂度在 邻接矩阵结构时候为 O（n2），邻接表结构时候为O（n）。
对于图的存储结构还有：十字链表、多重邻接表等等。
==================================================================
算法学习记录-图(DFS BFS)的更多相关文章
- 算法学习记录-图——最短路径之Dijkstra算法
在网图中,最短路径的概论: 两顶点之间经过的边上权值之和最少的路径,并且我们称路径上的第一个顶点是源点,最后一个顶点是终点. 维基百科上面的解释: 这个算法是通过为每个顶点 v 保留目前为止所找到的从 ...
- 算法学习记录-图——最小生成树之Kruskal算法
之前的Prim算法是基于顶点查找的算法,而Kruskal则是从边入手. 通俗的讲:就是希望通过 边的权值大小 来寻找最小生成树.(所有的边称为边集合,最小生成树形成的过程中的顶点集合称为W) 选取边集 ...
- 算法学习记录-图——应用之关键路径（Critical Path）
之前我们介绍过,在一个工程中我们关心两个问题: (1)工程是否顺利进行 (2)整个工程最短时间. 之前我们优先关心的是顶点(AOV),同样我们也可以优先关心边(同理有AOE).(Activity On ...
- 算法学习记录-图——最小路径之Floyd算法
floyd算法: 解决任意两点间的最短路径的一种算法,可以正确处理有向图或负权的最短路径问题,同时也被用于计算有向图的传递闭包. 设为从到的只以集合中的节点为中间节点的最短路径的长度. 若最短路径经过 ...
- 算法学习记录-图——最小生成树之prim算法
一个连通图的生成树是一个极小的连通子图,它包含图中全部的顶点(n个顶点),但只有n-1条边. 最小生成树:构造连通网的最小代价(最小权值)生成树. prim算法在严蔚敏树上有解释,但是都是数学语言,很 ...
- 算法学习记录-图——应用之拓扑排序（Topological Sort）
这一篇写有向无环图及其它的应用: 清楚概念: 有向无环图(DAG):一个无环的有向图.通俗的讲就是从一个点沿着有向边出发,无论怎么遍历都不会回到出发点上. 有向无环图是描述一项工程或者系统的进行过程的 ...
- 算法学习导图+经典排序算法PHP实现
周末抽时间整理下算法,完整导图可点击下面链接获取. 点我看完整算法导图 八种排序算法的php实现 代码如下 拷贝后可直接运行 先上个运行后的图 代码:(有的自己些的 有的根据网友整理) <?ph ...
- Manacher回文串算法学习记录
FROM: http://hi.baidu.com/chenwenwen0210/item/482c84396476f0e02f8ec230 #include<stdio.h> #inc ...
- 算法系列之图--DFS
深度优先搜索使用的策略是,只要与可能就在图中尽量“深入”.DFS总是对最近才发现的结点v出发边进行探索,知道该结点的所有出发边都被发现为止.一旦v的所有出发边都被发现了,搜索就回溯到v的前驱结点(v是 ...
随机推荐
- UG 常用设置
Q01:UG制图,添加基本视图之后的中心线怎么去掉? A01:“菜单-->文件-->首选项-->制图-->视图-->公共-->常规-->□带中心线创建”,取消 ...
- python学习之串口编程
# coding=utf-8import serial ser=serial.Serial('com1',9600)ser.write(b"hello")while 1: ser. ...
- Linux 安装reids
1.下载: wget http://download.redis.io/releases/redis-3.0.0.tar.gz 2.解压: .tar.gz 3.安装: cd /redis- make ...
- 惊人的CSS和JavaScript动画logos例子
https://codepen.io/lindell/pen/mEVgJP Stack Overflow logo是我最喜欢的logo之一,因为它非常简单,但易于识别.并且这个片段动画点击预览Stac ...
- react之——render prop
在react “从上至下的数据流原则” 背景下,常规的消息传递机制就是通过prop属性,把父级数据传递给子级,这样一种数据流通模式决定了——数据的接收方子组件要被”硬植入“进数据的数据的给予方父组件, ...
- 从零开始利用vue-cli搭建简单音乐网站（五）
上一篇文章讲到的是如何利用mongoose从数据库读取数据然后更新页面,接下来要实现的就是用户注册登录功能,这个功能涉及到的东西太多了,今天只实现了登录功能,登陆之后更新导航条界面,最后效果如下: 登 ...
- JS基础1 — 代码要注意的一些问题
1.在一对 <script></script> 标签中,有错的js代码,那么该错误代码后面的代码不会执行. 例子:<script> alert("He ...
- 【javascript】2017-9-12 腾讯笔试小Q升序算法
刚做完笔试,腾讯笔试系统真的不友好,作为一个前端,我只会用js写编程题,然而,然而腾讯笔试系统连js输入函数都没给,还不准跳出页面,那个调试结果一直显示错误,我一直找不到错误在哪,心累. 只做了一道笔 ...
- JMeter3.2入门使用教程
JMeter3.2入门使用教程 背景说明 1.1. 背景简介 JMeter是Apache软件基金会下的一个开源项目,纯java开发的应用工具,可以作为进行负载和压力测试的工具来使用.从最开始时被设计成 ...
- 在Windows 10删除百度云盘的盘符
1点击微软图标不放,然后点击R 打开运行命令 2输入 Regedit 进入注册表 3找到以下路径:HKEY_LOCAL_MACHINE SOFTWARE Microsoft Windows ...