AVL树插入和删除

一、AVL树简介

AVL树是一种平衡的二叉查找树。

平衡二叉树（AVL 树）是
一棵空树，或者
是具有下列性质的二叉排序树：
    1它的左子树和右子树都是平衡二叉树，
    2且左子树和右子树高度之差的绝对值不超过 1。

定义平衡因子（BF）为该结点左子树的高度减去右子树的高度所得的高度差；AVL 树任一结点平衡因子只能取-1，0，1；

二、AVL树插入

插入：先查找被插入元素，如果存在，则不操作；如果不存在，则插入。

插入后就是调整和选择的问题。

我们先看一下我们会面临怎么样的问题：

离插入点最近的失衡点可能很近，

也可能很远，所以我们要以下面这种模型思考。

可能的旋转有四种

1 LL型

2 LR型

3 RR型

4 RL型

为什么会只有这四种情况

无非是

失衡点BF=2，左节点BF=1，LL；

失衡点BF=2，左节点BF=-1，LR；

失衡点BF=-2，右节点BF=-1，RR；

失衡点BF=-2，右节点BF=1，RL；

所以写程序时，只要找到失衡点，根据BF就能判断该执行哪种旋转。

还有点就是如何计算BF，程序的参考http://blog.sina.com.cn/s/blog_6c014ac00100l35o.html

三、AVL树删除

一般查找二叉树删除节点

删除的方案有很多，但一般都会旋转下面这种，因为对整棵树各个分支深度的影响较小。

a.当被删除节点n是叶子节点，直接删除

b.当被删除节点n只有一个孩子，删除n，用孩子替代该节点的位置

c.当被删除结点n存在左右孩子时，真正的删除点应该是n的中序遍在前驱，或者说是左子树最大的节点，之后n的值替换为真正删除点的值。这就把c归结为a，b的问题。

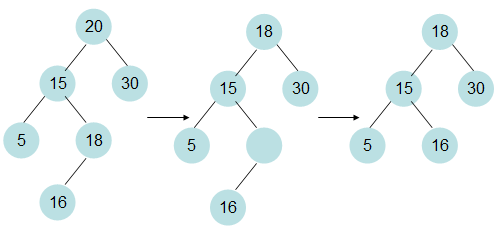
有了上面的规则，再结合http://www.cnblogs.com/Clingingboy/archive/2010/10/09/1846865.html即可

参考文章

http://blog.csdn.net/gabriel1026/article/details/6311339

http://blog.sina.com.cn/s/blog_6c014ac00100l35o.html

http://www.cnblogs.com/Clingingboy/archive/2010/10/09/1846865.html