PHP面试：说下什么是堆和堆排序？

堆是什么？

堆是基于树抽象数据类型的一种特殊的数据结构，用于许多算法和数据结构中。一个常见的例子就是优先队列，还有排序算法之一的堆排序。这篇文章我们将讨论堆的属性、不同类型的堆以及
堆的常见操作。另外我们还将学习堆排序，并将使用SPL实现堆。

根据定义，堆是一个拥有堆特性的树形数据结构。如果父节点大于子节点，那么它被称为最大堆，如果父节点小于子节点，则称为最小堆。下图是最大堆的例子

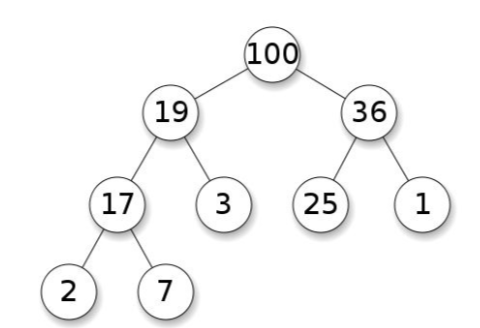
我们看根节点，值100大于两个子节点19和36。对于19来说，该值大于17和3。其他节点也适用相同的规则。我们可以看到，这棵树没有完全排序。但重要的事实是我们总能找到树的最大值或最小值，在许多特殊的情况下这是非常有用的。

堆结构有很多种，如二叉堆、B堆、斐波那契堆、三元堆，树堆、弱堆等。二叉堆是堆实现中最流行的一种。二叉堆是一个完全二叉树（不了解二叉树的朋友可以看PHP实现二叉树），树的所有内部节点都被完全填充，最后一层可以完全填充的或部分填充。对于二叉堆，我们可以在对数时间复杂度内执行大部分操作。

堆的操作

堆是一个特殊的树数据结构。我们首先根据给定的数据构建堆。由于堆有严格的构建规则，所以我们每一步操作都必须满足这个规则。下面是堆的一些核心操作。

• 创建堆
• 插入新值
• 从堆中提取最小值或最大值
• 删除一个值
• 交换

从给定的项或数字集合创建堆需要我们确保堆规则和二叉树属性得到满足。这意味着父节点必须大于或小于子节点。对于树中的所有节点，都需要遵守这个规则。同样，树必须是一个完全的二叉树。在创建堆时，我们从一个节点开始，并向堆中插入一个新节点。

当插入节点操作时，我们不能从任意节点开始。插入操作如下

• 将新节点插入堆的底部
• 检查新节点和父节点的大小顺序，如果它们是正确的顺序，停止。
• 如果它们不是正确的顺序，交换它们然后继续前一步的检查。这一步骤与前一步一起被称为筛分或上升，等等。

提取操作（最小或最大）即从堆中取出根节点。在此之后，我们必须执行下列操作以确保剩余节点然仍符合堆的特点。

• 从堆移动最后一个节点作为新根
• 将新根节点与子节点进行比较，如果它们处于正确的顺序，则停止。
• 如果不是，则将根节点与子节点交换（当是小根堆时为最小子节点，当大根堆时为最大子节点）并继续前面的步骤。这一步与前一个步骤一起被称为下堆。

在堆中，一个重要的操作是交换。现在我们将使用PHP7来实现二叉堆。

namespace DataStructure\Heap;

class MaxHeap
{
    public $heap;
    public $count;

    public function __construct(int $size)
    {
        //初始化堆
        $this->heap = array_fill(0, $size, 0);
        $this->count = 0;
    }

    public function create(array $arr = [])
    {
        array_map(function($item){
            $this->insert($item);
        }, $arr);
    }

    public function insert(int $data)
    {
        //插入数据操作
        if ($this->count == 0) {
            //插入第一条数据
            $this->heap[0] = $data;
            $this->count = 1;
        } else {
            //新插入的数据放到堆的最后面
            $this->heap[$this->count++] = $data;
            //上浮到合适位置
            $this->siftUp();
        }
    }

    public function display()
    {
        return implode(" ", array_slice($this->heap, 0));
    }

    public function siftUp()
    {
        //待上浮元素的临时位置
        $tempPos = $this->count - 1;
        //根据完全二叉树性质找到副节点的位置
        $parentPos = intval($tempPos / 2);

        while ($tempPos > 0 && $this->heap[$parentPos] < $this->heap[$tempPos]) {
            //当不是根节点并且副节点的值小于临时节点的值，就交换两个节点的值
            $this->swap($parentPos, $tempPos);
            //重置上浮元素的位置
            $tempPos = $parentPos;
            //重置父节点的位置
            $parentPos = intval($tempPos / 2);
        }
    }

    public function swap(int $a, int $b)
    {
        $temp = $this->heap[$a];
        $this->heap[$a] = $this->heap[$b];
        $this->heap[$b] = $temp;
    }

    public function extractMax()
    {
        //最大值就是大跟堆的第一个值
        $max = $this->heap[0];
        //把堆的最后一个元素作为临时的根节点
        $this->heap[0] = $this->heap[$this->count - 1];
        //把最后一个节点重置为0
        $this->heap[--$this->count] = 0;
        //下沉根节点到合适的位置
        $this->siftDown(0);

        return $max;
    }

    public function siftDown(int $k)
    {
        //最大值的位置
        $largest = $k;
        //左孩子的位置
        $left = 2 * $k + 1;
        //右孩子的位置
        $right = 2 * $k + 2;

        if ($left < $this->count && $this->heap[$largest] < $this->heap[$left]) {
            //如果左孩子大于最大值，重置最大值的位置为左孩子
            $largest = $left;
        }

        if ($right < $this->count && $this->heap[$largest] < $this->heap[$right]) {
            //如果右孩子大于最大值，重置最大值的位置为左孩子
            $largest = $right;
        }

        //如果最大值的位置发生改变
        if ($largest != $k) {
            //交换位置
            $this->swap($largest, $k);
            //继续下沉直到初始位置不发生改变
            $this->siftDown($largest);
        }
    }
}

复杂度分析

因为不同种类的堆有不同的实现，所以各种堆实现也有不同的复杂度。但是有一个堆的操作在各类实现中都是O(1)的复杂度，就是获取最大值或者最小值。我看来看下二分堆的复杂度分析。

操作	平均复杂度	最坏复杂度
Search	O(n)	O(n)
Insert	O(1)	O(log n)
Delete	O(log n)	O(log n)
Extract	O(1)	O(1)

因为二叉堆不是完全排序的，所以搜索操作会比二叉搜索树花更多的时间。

堆与优先队列

一个最常用的操作就是将堆当作优先队列来使用。在PHP实现栈和PHP实现队列中，我们已经了解到优先队列是一种根据元素权重而不是入队顺序来进行出队操作的结构。我们已经用链表实现优先队列和Spl实现优先队列,现在我们使用堆来实现优先队列。

namespace DataStructure\Heap;

class PriorityQueue extends MaxHeap
{
    public function __construct(int $size)
    {
        parent::__construct($size);
    }

    public function enqueue(int $val)
    {
        parent::insert($val);
    }

    public function dequeue()
    {
        return parent::extractMax();
    }
}

堆排序

在堆排序中，我们需要用给定的值构建一个一个堆。然后连续的检查堆的值以确保任何时候整个堆都是排序的。在正常的堆结构中，我们每当插入一个新的值到合适位置之后就停止检查，但是在堆排序中，只要有下一个值，我们就不断的去检查构建堆。伪代码如下：

HeapSort(A)
BuildHeap(A)
for i = n-1 to 0
swap(A[0],A[i])
n = n - 1
Heapify(A, 0)

BuildHeap(A)
n = elemens_in(A)
for i = floor(n / 2) to 0
Heapify(A, i)

Heapify(A, i)
left = 2i+1;
right = 2i + 2;
max = i

if (left < n and A[left] > A[i])
max = left
if (right < n and A[right] > A[max])
max = right

if (max != i)
swap(A[i], A[max])
Heapify(A, max)

从上面的伪代码可以看到，堆排序的第一步就是构建一个堆。每次我们向堆中添加新的元素，我们都调用heapify来满足堆的特性。一旦堆构建好之后，我们对所有的元素都进行检查，下面使用PHP的实现堆排序。完整的代码可以点这里查看。

```
function heapSort(&$arr)
{
$length = count($arr);
buildHeap($arr);
$heapSize = $length - 1;
for ($i = $heapSize; $i >= 0; $i--) {
list($arr[0], $arr[$heapSize]) = [$arr[$heapSize], $arr[0]];
$heapSize--;
heapify(0, $heapSize, $arr);
}
}

function buildHeap(&$arr)

{

$length = count($arr);

$heapSize = $length - 1;

for ($i = ($length / 2); $i >= 0; $i--) {

heapify($i, $heapSize, $arr);

}

}

function heapify(int $k, int $heapSize, array &$arr)

{

$largest = $k;

$left = 2 * $k + 1;

$right = 2 * $k + 2;

if ($left <= $heapSize && $arr[$k] < $arr[$left]) {
    $largest = $left;
}

if ($right <= $heapSize && $arr[$largest] < $arr[$right]) {
    $largest = $right;
}

if ($largest != $k) {
    list($arr[$largest], $arr[$k]) = [$arr[$k], $arr[$largest]];
    heapify($largest, $heapSize, $arr);
}

}

<p>堆排序的时间复杂度为O(nlog n)，空间复杂度为O(1)。对比归并排序，堆排序有更好的表现。</p>
<h3>PHP中的SplHeap、SplMinHeap和SplMaxHeap</h3>
<p>当然，方便的PHP内置的标准库已经帮助我实现了堆，你可以通过<code>SplHeap</code>、<code>SplMinHeap</code>、<code>SplMaxHeap</code>来使用它们。</p>
<h3>更多内容</h3>
<p>PHP基础数据结构专题系列目录: <a href="https://github.com/xx19941215/light-tips" rel="nofollow noreferrer">地址</a>。主要使用PHP语法总结基础的数据结构和算法。还有我们日常PHP开发中容易忽略的基础知识和现代PHP开发中关于规范、部署、优化的一些实战性建议，同时还有对Javascript语言特点的深入研究。</p>

原文地址：https://segmentfault.com/a/1190000016067129