LuoguP1606 [USACO07FEB]荷叶塘Lilypad Pond 【最短路】By cellur925

最短路好题！】

参考资料：学长 https://blog.csdn.net/TSOI_Vergil/article/details/52975779 学长太强了！！！%%%

题目传送门

==================算法部分=====================

我们读完题后，就能感受到浓浓的最短路氛围。我们可以将水与莲花间连边，水水间连边，边权为1；莲花间各自连边，边权为0。这样我们跑完一遍spfa后，就能得到摆放莲花的最小数量。但是第二问就很棘手，聪明的你也许会说跑一遍最短路计数就行了。但其实这是错误的算法。

比如在这张图中。正方形是莲花，圆是水（后连的莲花）

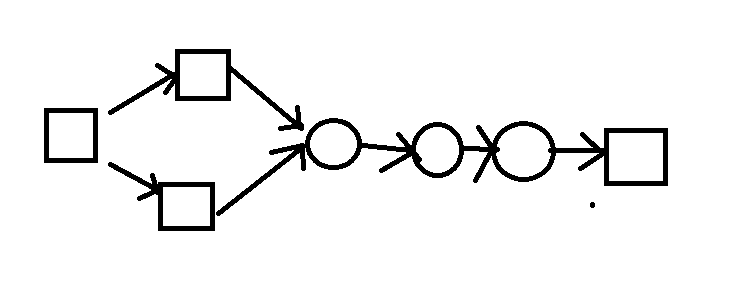
最短路条数为2，但有3个莲花。

或者更理性的说，如果经过的水面相同而经过的莲花不同，会被算作是不同的最短路，而实际上方案却是一样的。

不同的最短路要求很低，只要经过的点有一点不同便不同。而适合本题的求解则是只能水面不同，已有的莲花不同不算不同，也就是说 跑最短路时只经过水面。

再冷静分析我们会发现已有的莲花间的边是无意义的，只是“为了保证连通性”。同理，除起点和终点外的莲花与水之间的边也是没有意义的。

所以 我们考虑重新建图，对于每个水，对它进行bfs，把它和它能到达的水连边（或作可达性标记）；将起点终点与水连边，这样跑最短路 。我们发现经过这样建图后最短路上的点除起点和终点是莲花之外，其余的点全是水，这样不同的最短路就对应着经过了不同的水，也就对应着不同的放莲花的方案。

以上有很多都参考Vergil学长的分析==

==================代码实现部分========================

然而算法说起来简单，实现就有些难了。学长给出的代码我太弱不能理解，于是便参考了金涛dalao的写法。从他的代码中对搜索有了更深理解。

先来观摩一下学长的代码，比较妙的地方是把矩阵的横纵坐标压成序号。

 #include<cstdio>

 #include<cstring>

 #include<algorithm>

 using namespace std;

 #define maxn 130005

 int n,m,g[][],sx,tx,sy,ty,l,cnt;

 int pre[maxn],last[maxn],other[maxn];

 int quex[],quey[],que[];

 const int dx[]={,,,,,-,-,-,-};

 const int dy[]={,-,,-,,-,,-,};

 int flag[][],dis[];

 bool vis[][],vist[maxn];

 long long f[];

 void connect(int x,int y)

 {

     l++;

     pre[l]=last[x];

     last[x]=l;

     other[l]=y;    

 }

 void bfs(int fx,int fy)

 {

     flag[fx][fy]=++cnt;

     int h=,t=;

     for (int i=;i<=;i++) 

     {

         int xx=fx+dx[i];

         int yy=fy+dy[i];

         if (xx<||xx>n||yy<||yy>m) continue;

         if (flag[xx][yy]==cnt) continue;

         flag[xx][yy]=cnt;

         if (g[xx][yy]!=&&g[xx][yy]!=) 

         {

             t++;

             quex[t]=xx;quey[t]=yy;

             int id1=(fx-)*m+fy;

             int id2=(xx-)*m+yy;

             if (vis[id1][id2]) continue;

             connect(id1,id2);

             connect(id2,id1);

             vis[id1][id2]=vis[id2][id1]=;    

         }

         else if (g[xx][yy]==)     

         {

             int id1=(fx-)*m+fy;

             int id2=(xx-)*m+yy;

             if (vis[id1][id2]) continue;

             connect(id1,id2);

             connect(id2,id1);

             vis[id1][id2]=vis[id2][id1]=;    

         }

     }

     while (h<=t) 

     {

         int x=quex[h],y=quey[h];h++;

         for (int i=;i<=;i++) 

         {

             int xx=x+dx[i];

             int yy=y+dy[i];

             if (xx<||xx>n||yy<||yy>m) continue;

             if (flag[xx][yy]==cnt) continue;

             flag[xx][yy]=cnt;

             if (g[xx][yy]==) 

             {

                 int id1=(fx-)*m+fy;

                 int id2=(xx-)*m+yy;

                 if (vis[id1][id2]) continue;

                 connect(id1,id2);

                 connect(id2,id1);

                 vis[id1][id2]=vis[id2][id1]=;

             }

             else if (g[xx][yy]!=&&g[xx][yy]!=) 

             {

                 t++;

                 quex[t]=xx;quey[t]=yy;    

             }

         }

     }

 }

 void spfa(void)

 {

     memset(dis,,sizeof dis);

     dis[(sx-)*m+sy]=;

     que[]=(sx-)*m+sy;

     int h=,t=;

     while (h<=t) 

     {

         int u=que[h];h++;

         vist[u]=;

         for (int p=last[u];p;p=pre[p]) 

         {

             int v=other[p];

             if (dis[v]>dis[u]+) 

             {

                 dis[v]=dis[u]+;    

                 if (!vist[v]) 

                 {

                     que[++t]=v;

                     vist[v]=;    

                 }

             }

         }

     }

 }

 void solve(void)

 {

     memset(vist,,sizeof vist);

     que[]=(sx-)*m+sy;f[que[]]=;

     int h=,t=;

     while (h<=t) 

     {

         int u=que[h];h++;

         for (int p=last[u];p;p=pre[p]) 

         {

             int v=other[p];

             if (dis[v]==dis[u]+) 

             {

                 f[v]+=f[u];

                 if (!vist[v]) 

                 {

                     que[++t]=v;

                     vist[v]=;    

                 }

             }

         }

     }

 }

 int main()

 {

     scanf("%d%d",&n,&m);

     for (int i=;i<=n;i++) 

         for (int j=;j<=m;j++) 

         {

             scanf("%d",&g[i][j]);

             if (g[i][j]==) {sx=i;sy=j;}

             if (g[i][j]==) {tx=i;ty=j;}

         }

     bfs(sx,sy);

     bfs(tx,ty);

     for (int i=;i<=n;i++) 

         for (int j=;j<=m;j++) 

             if (g[i][j]==) bfs(i,j);

     spfa();

     if (dis[(tx-)*m+ty]>1e7) 

     {

         printf("-1\n");

         return ;

     }

     printf("%d\n",dis[(tx-)*m+ty]-);

     solve();

     printf("%lld\n",f[(tx-)*m+ty]);

     return ;    

 }

Vergil

金涛的代码就比较亲民了Orz。我仿照他的代码写了一份。注释里有解释。

 #include<cstdio>
 #include<queue>
 #include<cstring>
 #include<algorithm>
 #include<utility>

 using namespace std;
 typedef long long ll;

 int n,m,bx,by,ex,ey;
 int mapp[][],dis[][];
 ll f[][];//记得开long long！！
 bool vis[][];
 bool able[][][][];
 int dx[]={,,,,,-,-,-,-};
 int dy[]={,-,-,,,,,-,-};

 void floodfill(int x,int y)
 {//洪水填充，也可以理解为bfs
     memset(vis,,sizeof(vis));
     queue<pair<int,int> > q;
     q.push(make_pair(x,y));
     while(!q.empty())
     {
         int nowx=q.front().first;
         int nowy=q.front().second;
         q.pop();
         for(int i=;i<=;i++)
         {
             int xx=nowx+dx[i];
             int yy=nowy+dy[i];
             if(xx<||xx>n||yy<||yy>m) continue;
             if(vis[xx][yy]) continue;//vis数组实际在检查是不是莲花，但我们要找水
             if(!mapp[xx][yy]||(xx==ex&&yy==ey))
                 able[x][y][xx][yy]=;//注意是x,y 我们洪水填充的目的是更新传进的x,y
 // able相当于连边了 效果一样
             else if(mapp[xx][yy]==)
                 q.push(make_pair(xx,yy)),vis[xx][yy]=;
 //如果是莲花，就是待扩展节点，加入队列
         }
     }
 }

 void spfa_work()
 {//边跑最短路边计数
     memset(vis,,sizeof(vis));
     queue<pair<int,int> >q;
     q.push(make_pair(bx,by));
     memset(dis,,sizeof(dis));
     vis[bx][by]=;dis[bx][by]=,f[bx][by]=;
     while(!q.empty())
     {
         int nowx=q.front().first;
         int nowy=q.front().second;
         q.pop();vis[nowx][nowy]=;
         for(int i=;i<=n;i++)
             for(int j=;j<=m;j++)
                 if(able[nowx][nowy][i][j])
                 {
                     if(dis[i][j]>dis[nowx][nowy]+)
                     {
                         dis[i][j]=dis[nowx][nowy]+;
                         f[i][j]=f[nowx][nowy];
                         if(!vis[i][j]&&(i!=ex||j!=ey))
                         {//终点就不用再扩展了
                             vis[i][j]=;
                             q.push(make_pair(i,j));
                         }
                     }
                     else if(dis[i][j]==dis[nowx][nowy]+)
                         f[i][j]+=f[nowx][nowy];
                 }
     }
 }

 int main()
 {
     scanf("%d%d",&n,&m);
     for(int i=;i<=n;i++)
         for(int j=;j<=m;j++)
         {
             scanf("%d",&mapp[i][j]);
             if(mapp[i][j]==) bx=i,by=j;
             if(mapp[i][j]==) ex=i,ey=j;
         }
     floodfill(bx,by);
 //从起点出发
     for(int i=;i<=n;i++)
         for(int j=;j<=m;j++)
             if(!mapp[i][j]) floodfill(i,j);
     spfa_work();
     if(dis[ex][ey]>)
     {//最多也才900个点
         printf("-1");
         return ;
     }
     else printf("%d\n%lld",dis[ex][ey]-,f[ex][ey]);
 //注意-1 以及lld
     return ;
 }

在这道题中学到了肥肠多的新想法，更深入理解了搜索算法。

本来最简单的dfsbfs我是不会的，但是学习了图论之后，就能感性理解，现在我们回过头去看那些最简单的：

bfs 我们常常使用队列实现，而我们要注意到，队列中的点都是待扩展节点。每次我们取出队头的顶点，遍历它能到达的全部状态。