HDU 5217 Brackets

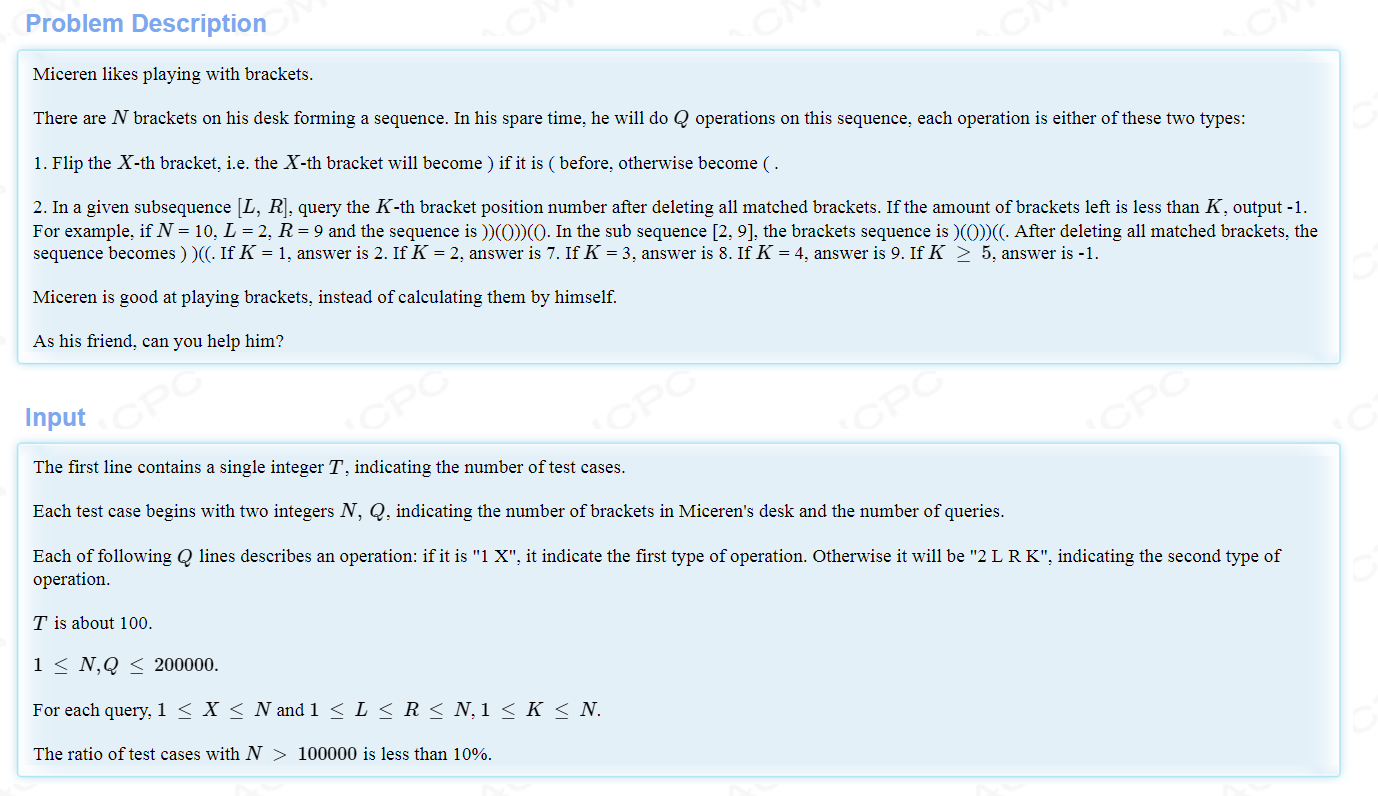
【题意概述】

　　给出一个有左括号和右括号的序列，左边的左括号和右边的右括号可以合并。现在要求你维护这个序列，支持两种操作：

　　1，翻转某个位置的括号；

　　2，查询区间[L,R]合并后第k个括号在原序列中的位置，如果k超过区间合并后的括号总数，输出-1.

【题解】

　　首先我们可以发现，对于一个区间，合并后的结果一定是若干个右括号、若干个左括号的形式。即))))(((((...

　　线段树上维护两个标记，区间左边的右括号数量cl、区间右边的左括号数量cr。合并的时候把左区间的cr和右区间的cl抵消一下，然后计算新的cl、cr即可。

　　这样对于询问，我们可以快速确定它是左括号还是右括号，或者不满足题意输出-1。但我们怎么求第k个左/右括号在原序列中的位置呢？我的做法是询问的时候把经过的各个区间记录一下，逐个区间查找，如果k落在当前区间，就进入线段树进行查找，走到叶子结点就是答案。也可以直接在线段树上查找，不把区间取出来。

　　

 #include<cstdio>
 #include<algorithm>
 #define rg register
 #define N 200010
 #define ls (u<<1)
 #define rs (u<<1|1)
 using namespace std;
 int T,n,m,f[N],s[N],cnt,rt;
 char c[N];
 struct tree{
     int l,r,cl,cr;
 }a[N<<];
 struct rec{
     int cl,cr;
 };
 inline int read(){
     int k=; char c=getchar();
     while(c<''||c>'')c=getchar();
     while(''<=c&&c<='')k=k*+c-'',c=getchar();
     return k;
 }
 inline void pushup(int u){
     a[u].cl=a[ls].cl; a[u].cr=a[rs].cr;
     int tmp=a[ls].cr-a[rs].cl;
     if(tmp>) a[u].cr+=tmp;
     else a[u].cl-=tmp;
 }
 void build(int u,int l,int r){
     a[u].l=l; a[u].r=r; a[u].cl=a[u].cr=;
     if(l<r){
         int mid=(l+r)>>;
         build(ls,l,mid); build(rs,mid+,r);
         pushup(u);
     }
     else{
         if(f[l]==) a[u].cr=; else a[u].cl=;
     }
 }
 void update(int u,int pos){
     if(a[u].l==a[u].r){
         a[u].cl^=; a[u].cr^=; return;
     }
     int mid=(a[u].l+a[u].r)>>;
     if(pos<=mid) update(ls,pos);
     else update(rs,pos);
     pushup(u);
 }
 rec query(int u,int l,int r){
     if(l<=a[u].l&&a[u].r<=r){
         s[++cnt]=u;
         rec tmp;
         tmp.cl=a[u].cl; tmp.cr=a[u].cr;
         return tmp;
     }
     int mid=(a[u].l+a[u].r)>>;
     rec ret,L,R; ret.cl=ret.cr=;
     if(l<=mid) ret=L=query(ls,l,r);
     if(r>mid) ret=R=query(rs,l,r);
     if(l<=mid&&r>mid){
         ret.cl=L.cl; ret.cr=R.cr;
         int tmp=L.cr-R.cl;
         if(tmp>) ret.cr+=tmp;
         else ret.cl-=tmp;
     }
     return ret;
 }
 int findl(int u,int k){
     if(a[u].l==a[u].r) return a[u].l;
     if(a[ls].cl>=k) return findl(ls,k);
     return findl(rs,k-a[ls].cl+a[ls].cr);
 }
 int findr(int u,int k){
     if(a[u].l==a[u].r) return a[u].l;
     if(a[rs].cr>=k) return findr(rs,k);
     return findr(ls,k-a[rs].cr+a[rs].cl);
 }
 int main(){
     T=read();
     while(T--){
         n=read(); m=read();
         scanf("%s",c+);
         for(rg int i=;i<=n;i++) if(c[i]=='(') f[i]=; else f[i]=;
         build(,,n);
         while(m--){
             int opt=read();
             if(opt==){
                 int x=read();
                 update(,x);
             }
             else{
                 int l=read(),r=read(),k=read(); cnt=;
                 rec tmp=query(,l,r);
                 if(tmp.cl+tmp.cr<k){
                     puts("-1");
                     continue;
                 }
                 if(tmp.cl>=k){
                     for(rg int i=;i<=cnt;i++){
                         if(a[s[i]].cl>=k){
                         rt=s[i]; break;
                         }
                         else k+=a[s[i]].cr-a[s[i]].cl;
                     }
                     printf("%d\n",findl(rt,k));
                 }
                 else{
                     k=tmp.cl+tmp.cr-k+;
                     for(rg int i=cnt;i;i--){
                         if(a[s[i]].cr>=k){
                             rt=s[i]; break;
                         }
                         else k+=a[s[i]].cl-a[s[i]].cr;
                     }
                     printf("%d\n",findr(rt,k));
                 }
             }
         }
     }
     return ;
 }