【学习笔记】OI玄学道—代码坑点

【学习笔记】OI玄学道—代码坑点

---

【目录】

• 【逻辑运算符的短路运算】
• 【\(cmath\) 里的贝塞尔函数】
• 【\(scanf\) 读入字符】
• 【\(cmath\) 中的 \(pow\) 函数】
• 【\(vector\) 的 \(size\) 函数】

---

一：【逻辑运算符的短路运算】

【运算规则】

&& 和 || 属于逻辑运算符。关于 && 和 || 的表达式的运算规则是这样的（用大写字母来表示表达式）：

\(A\) || \(B\)

只要任意一个表达式为 \(true\)，则整个表达式的运算结果为 \(true(1)\)。

\(A\) && \(B\)

仅当所有表达式都为 \(true(1)\) ，整个表达式的运算结果才为 \(true(1)\) 。

当任意一个表达式为 \(false(0)\) ，整个表达式的运算结果则为 \(false(0)\) 。

【短路运算】

&& 和 || 的短路运算，是指如果在进行前面的表达式的运算过程，通过判断已经明确的知道整个表达式的结果，那么就不会进行后面表达式的运算判断。例如：

\(A\) || \(B\) || \(C\) \(....\) || \(Z\)

如果 \(A\) 的运算结果为 \(true(1)\) ，则整个表达式的结果为 \(true(1)\) ，同时不会再对后面的 \(B\)、\(C\) 到表达式 \(Z\) 进行运算判断。

如果 \(A\) 的运算结果为 \(false(0)\) ，则根据 \(B\) 的运算结果继续判断。

\(A\) && \(B\) && \(C\) \(....\) && \(Z\)

如果 \(A\) 的运算结果为 \(true(1)\) ，则整个表达式的结，如果 \(A\) 的运算结果为 \(false(0)\) ，则整个表达式的结果为 \(false(0)\) ，同时不会再对后面的 \(B\) 、表达式3到表达式n进行运算判断。如果 \(A\) 的运算结果为 \(true(1)\) ，则根据 \(B\) 的运算结果继续判断。

【小技巧】

把能快速确定整个表达式结果 \(true(1)\) 或 \(false(0)\) 的表达式放在前面，这样由于短路运算后面的表达式可能不会被运算到，节省处理器的运算时间。

【坑点】

由于 && 和 || 的表达式存在短路运算现象，在短路之后不会对后面的表达式进行运算，所以含有 && 和 || 的表达式最好不要进行变量的赋值和运算操作，可以先计算好每个表达式的结果，直接拿结果进行 && 和 || 的运算。

在代码编写的时候就要注意这一点，以防由于 && 和 || 的短路运算导致写出来的代码运算结果与预期的不同。

（以上摘自 \(bulebin\) 大佬，原文链接）

【我心伤悲，莫知我哀】

曾经某个蒟蒻在尝试压行的时候，欣喜O(∩_∩)O~~地发现：

要是把赋值的操作放到判断里面，可以节省大量代码行.

然后(；′⌒`)，

......

就没有然后了 (╯ ﹏ ╰)

没错，就是我，而且知道现在才知道当初为什么会错 /(ㄒoㄒ)/~~

好桑心(ㄒ﹏ㄒ)

.......

食物链 \([NOI2001]\) \([P2024]\)

（压行前）

if(a>1){//b吃c
    if(b==c){++ans;continue;};
    //食物        天敌          同类
    b1=find(b),b2=find(b+n),b3=find(b+2*n);
    c1=find(c),c2=find(c+n),c3=find(c+2*n);
    if(b2==c3||b3==c1||b3==c3){++ans;continue;};
    f[b1]=f[c3],f[c2]=f[b3],f[b2]=f[c1];
}
else{//b,c是同类
    //食物        天敌          同类
    b1=find(b),b2=find(b+n),b3=find(b+2*n);
    c1=find(c),c2=find(c+n),c3=find(c+2*n);
    if(b1==c3||b2==c3||c1==b3||c2==b3){++ans;continue;};
    f[b3]=f[c3],f[b1]=f[c1],f[b2]=f[c2];
}

（压行后）

if(a>1){
    if((b==c)||(b2=find(b+n))==(c3=find(c+2*n))||(b3=find(b+2*n))==(c1=find(c))||b3==c3)++ans;
    else f[find(b)]=f[c3],f[find(c+n)]=f[b3],f[b2]=f[c1];
}
else{
    if((b1=find(b))==(c3=find(c+2*n))||(b2=find(b+n))==c3||(c1=find(c))==(b3=find(b+2*n))||(c2=find(c+n))==b3)++ans;
    else f[b3]=f[c3],f[b1]=f[c1],f[b2]=f[c2];
}

二：【cmath里的贝塞尔函数】

你有使用过 \(cmath\) 函数库吗？

你有定义全局变量的习惯吗？

你有定义过 \(y0,j0\) 变量吗？

当你同时具备以上条件时，恭喜你，踩雷了。

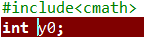
在 \(camth\) 源代码的 \(262\) 至 \(267\) 行有这样一段代码：

_CRTIMP double __cdecl j0 (double) __MINGW_ATTRIB_DEPRECATED_MSVC2005;
_CRTIMP double __cdecl j1 (double) __MINGW_ATTRIB_DEPRECATED_MSVC2005;
_CRTIMP double __cdecl jn (int, double) __MINGW_ATTRIB_DEPRECATED_MSVC2005;
_CRTIMP double __cdecl y0 (double) __MINGW_ATTRIB_DEPRECATED_MSVC2005;
_CRTIMP double __cdecl y1 (double) __MINGW_ATTRIB_DEPRECATED_MSVC2005;
_CRTIMP double __cdecl yn (int, double) __MINGW_ATTRIB_DEPRECATED_MSVC2005;

实际上这个叫做 \(Bessel\) 函数。

所以写代码时应注意不要定义 \(j0,j1,jn,y0,y1,yn\) 这些变量，但仅限于全局变量，如果是局变量的话，尽情的使用吧。

【参考文献】

贝塞尔函数 \(Bessel\)（原理与实现）

三：【scanf读入字符】

由于 \(scanf\) 的高效，我们通常喜欢用 \(scanf\) 来读入，然而这东西也会坑人，例如这种情况：

在每行的读入中，由一个字符作为开头。

\(cin\) 在读入时会跳过空格和换行，\(scanf\) 只会跳过空格，而不会跳过换行，所以如果直接在每行读入整数之前写 \(scanf(“\%c”,\&ch)\) 的话\(.......\)

改成 \(scanf(“\_\%c”,\&ch)\) 就可以了（下划线处是一个空格）

四：【cmath中的pow函数】

\(camth\) 函数库里的 \(pow\) 函数精度弱的惊人，可能本地自己测数据全对，交上去全 \(WA\)，所以快速幂很重要，不能为了偷懒直接用 \(pow\)，风险较大一般承受不起。

---

五：【vector的size函数】

\(size()\) 函数可返回 \(vector\) 大小，其返回值类型为 \(size\_type\)，应强制转换成 \(int\) 后再使用，例：

int n=Q.size()-1;
for(int i=0;i<=n;++i);
for(int i=0;i<=(int)(Q.size()-1);++i);

---

\(To\) \(be\) \(continued...\)