noip模拟赛 戏

【问题背景】
zhx 和他的妹子（们） 做游戏。
【问题描述】
考虑 N 个人玩一个游戏，任意两个人之间进行一场游戏（共 N*(N-1)/2 场），
且每场一定能分出胜负。
现在， 你需要在其中找到三个人构成“剪刀石头步”局面： 三个人 A， B， C
满足 A 战胜 B， B 战胜 C， C 战胜 A。

【输入格式】
第一行一个正整数 N， 表示参加游戏的人数。
接下来 N 行， 每行 N 个数 0/1，中间没有空格隔开。第 i 行第 j 列数字为 1
表示 i 在游戏中战胜了 j。 所有对角线元素（即第 i 行第 i 个元素） 为 0， 保证数
据合法。
【输出格式】
如果存在三个人构成“剪刀石头布”局面， 输出三个人的编号（从 1 开始）。
如果不存在这样的三个人， 输出一个数-1。
【样例输入】
5
00100
10000
01001
11101
11000
【样例输出】
1 3 2
【数据规模与约定】

分析：今天才知道这种图叫竞赛图，还是第一次接触它.

首先，竞赛图中是没有两元环的，两个点不可能互指.并且竞赛图中一条任意长度的环都可以通过某种变换变成3元环，也就是题目要求的.具体是怎么变换呢？考虑这样一个环：

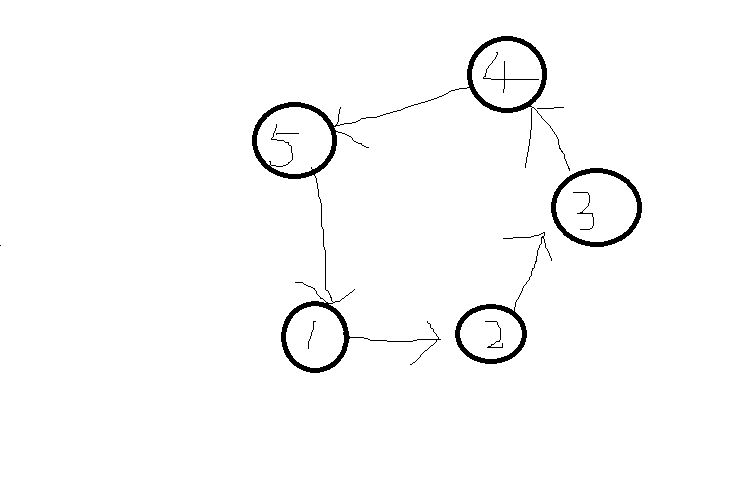
考虑前3个点1、2、3,如果1、3之间的连边是从3指向1，那么就找到了一个3元环，否则，我们完全可以不考虑2这个点，继续考虑1,3,4,检查1,4的连边，这就和1,2,3这种情况一样了，每次把环的长度-1，由于不存在2元环，所以最后一定可以找到一个三元环.

接下来的任务就是怎么要找到一个任意长度的环.

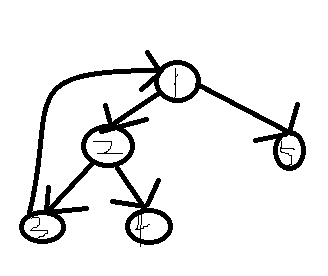
把dfs走的图看作一棵“树”，如果子节点有边连向祖先，那么就形成了环.将dfs时的vis数组改一下就可以了,vis[i] = 0表示i没有访问过,i=1表示正在访问i或者i的子树，i=2表示i的子树访问完了.如果下一个点vis=1，那么就找到一个环了.维护一个栈，记录一个时间戳，访问到新节点就加入到栈中，子树访问完了就退出来，找到环后就把栈中对应下标的元素一复制就好了.

一个比较重要的思想是把其它的所有不满足条件的情况都给排除掉，一步步接近我们的目标.就好比找3元环，首先证明2元环是不存在的，然后证明大于3元环的一定可以找到3元环，把问题一步步缩小就能找到答案.

#include <map>
#include <queue>
#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>

using namespace std;

int n, a[][], dfs_clock, s[], time[], head[], to[ * ], nextt[ * ], tot = ;
int vis[], top, ans[], cnt;

bool flag = false;

void add(int x, int y)
{
    to[tot] = y;
    nextt[tot] = head[x];
    head[x] = tot++;
}

void dfs(int u)
{
    if (flag)
        return;
    vis[u] = ;
    s[++top] = u;
    time[u] = top;
    for (int i = head[u]; i; i = nextt[i])
    {
        int v = to[i];
        if (!vis[v])
            dfs(v);
        if (vis[v] == )
        {
            flag = ;
            for (int j = time[v]; j <= top; j++)
                ans[++cnt] = s[j];
            return;
        }
    }
    vis[u] = ;
    s[top--] = ;
}

int main()
{
    scanf("%d", &n);
    for (int i = ; i <= n; i++)
        for (int j = ; j <= n; j++)
        {
            scanf("%1d", &a[i][j]);
            if (a[i][j])
                add(i, j);
        }
    for (int i = ; i <= n; i++)
        if (!vis[i])
        {
            dfs(i);
            if (flag)
                break;
        }
    if (!flag)
        printf("-1");
    else
    {
        for (int i = ; i < cnt; i++)
            if (a[s[i + ]][s[]])
            {
                printf("%d %d %d\n", s[], s[i], s[i + ]);
                break;
            }
    }

    return ;
}