基于R-Tree的最近邻查询

转自基于R-Tree的最近邻查询

BAB(Branch．and．Band)算法是由Nick Roussopoulousnl等人于1995年提出的，是最早的基于R．树的静态最近邻查询算法。该算法使用MINDIST和MINMAXDIST两个距离作为查询过程中的判断条件，对R树进行深度优先

搜索以查找最近邻，适用于基于静态对象的最近邻搜索。BAB思想已经被广泛的应用于人工智能以及运筹学等领域。如果搜索顺序和剪枝的规则选取适当，可以有效的减少系统在大规模空间搜索过程中的结点访问数目。

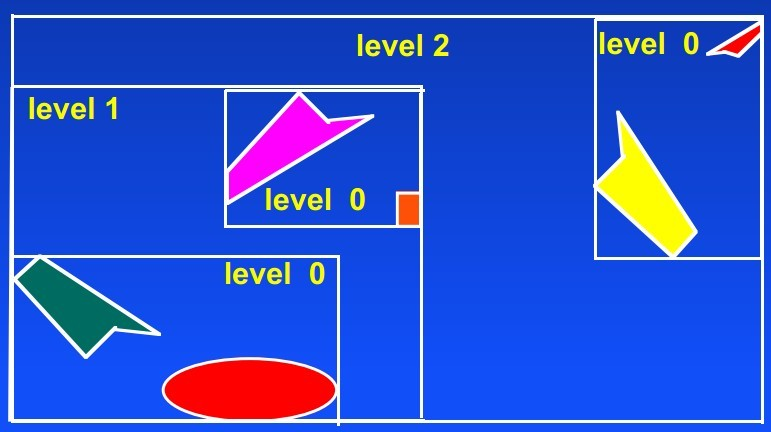
一、The MBR Face Property

Lemma:Every face of any MBR contains at least one point of an
actual spatial object 如图：

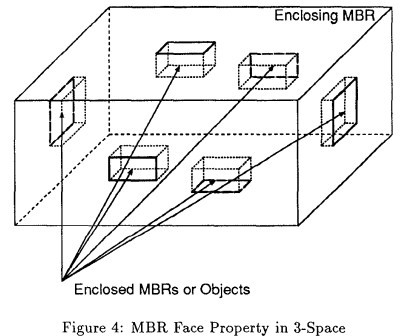
二、距离度量MINDIST和MINMAXDIST

为了减少计算量，文中的距离都以实际欧式距离的平方为标准。

给定一个查询点p及包含在一个MBR中的空间数据对象O，定义两个距离MINDIST和MINMAXDIST作为最近邻的度量和约束。其中：

MINDIST(P,R):  the shortest distance from P to R

MINMAXDIST(P,R)：the minimum over all dimensions distance from P  to the furthest point of the closest face of the R

Theorem:

1. Any object O in R has distance from P that is at least as large as MINDIST

2.There exists at least one object within R with distance <= to MINMAXDIST

so：

MINDIST(P,R)  <=  NN(P)  <=  MINMAXDIST(P,R)            （1）

三、MINDIST和MINMAXDIST的计算

    MINDIST：

1.查询点p在R内或R的边界上则MINDIST=0

2.查询点p在R外，若最短距离距离（p到R的边）存在，则MINDIST=p到R的边的最短距离

否则，MINDIST=p到R的顶点的最短最短距离。

MINMAXDIST的计算过程：

1.找出与第k轴垂直的并且离查询点p最近的面，记为H

2.选择从查询点p到面H中距离最远的那个点，记为a

3.计算查询点p到点a的距离,记为dk

4.对每个坐标轴重复步骤1-步骤3，记计算所得距离为d1，d2，...dk

5.从所有计算所得距离中选出最小的那一个，即MINMAXDIST

例如：下图中查询点p在外接矩形R之外，根据上面的计算步骤我们可得：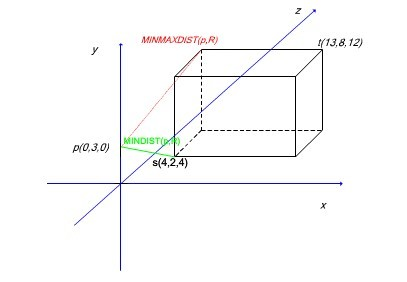

X轴：找到点（4,8,12）  计算p到此点的距离的平方dx=185

y轴：找到点（13,2,12） 计算p到此点的距离的平方dy=313

z轴：找到点（13,8,4）  计算p到ci点的距离的平方dz=210

所以此例中的MINMAXDIST（p，R）=185

下图表示了二维空间中点P与几个最小包含矩形MBR的MINDIST和MINMAXDIST的一个例子。二维空间中共有四个MBR，点P到它们的MINDIST和MINMAxDIST值在图中用箭头标出。如果点P位于MBR内部MINDIST值为0。

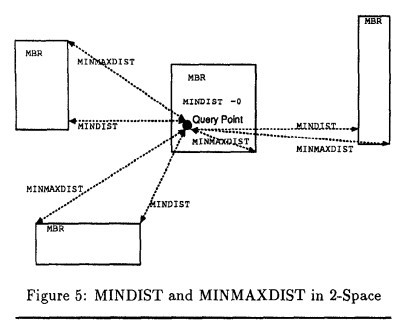
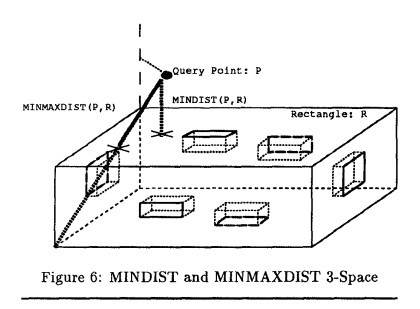
下图表示了三维空间中的MINDIST和MINMAXDIST。

四、减枝策略

由以上讨论，剪枝过程按以下三种策略进行：

1．若一个最小包含矩形E的MINDIST值大于另一个最小包含矩形E’的MINMAXDIST值，则最小包含矩形E内不可能包含最近邻对象。所以E可以被忽略。该策略用于向下剪枝。

2．若查询点q到某对象O的距离值大于点q到最小包含矩形E的MINMAXDIST的值则对象O被丢弃。因为最小包含矩形层此时包含距离查询点口更近的对象O’。该策略用于向上剪枝。

3．若最小包含矩形E的MINDIST值大于查询点g到某对象O的距离，则E被丢弃，因为最小包含矩形E内部不可能包含比对象O更近的对象。该策略用于向上剪枝。

尽管规定在向下剪枝时用MINMAXDIST进行判断，然而在某些情况下使用MINDIST效果会更好。例如当R树的结点中不存在死区或者死区很少时，在R树的某一层上MINDIST相对于MINMAxDIST而言是查询点到最近邻对象实际距离的更好估计。此时使用MINDIST可以剪掉更多无关的候选MBR。

五、Branch and Bound算法

该算法从根结点开始向下访问各层MBR。算法中首先假定最近邻距离Nearest为无穷大。随着搜索的下降，对每个最新访问的非叶结点首先计算出其中所有的MBR的MINDIST值，并将这些值排序后放入活动分支链表ABL(Active
Branch
List)中，接着对ABL运用剪枝策略1和策略2来移除不必要的分支。算法在ABL上重复进行直至ABL为空。每次重复过程中都选择链表中的下一个分支，并在与该分支的MBR相应的结点上递归进行以上过程。对于叶结点算法对每个对象调用一个特定类型的距离函数，并将计算出的值逐个与Nearest比较，选择其中更小的值替换Nearest。在递归过程返回时使用这个新的最近邻距离的估计值作为判断条件，采用策略3剪枝以移除ABL中所有MINDIST值大子Nearest的MBR所在的分支。

算法伪代码：

参考：

Nearest Neighborhood Queries.Nick Roussopoulos等.

http://www.doc88.com/p-146668818114.html

http://zh.scribd.com/doc/73414427/32/Fig-4-4-Example-of-MINDIST-and-MINMAXDIST