PTA数据结构与算法题目集(中文) 7-32

PTA数据结构与算法题目集(中文)  7-32

7-32 哥尼斯堡的“七桥问题” (25 分)

 

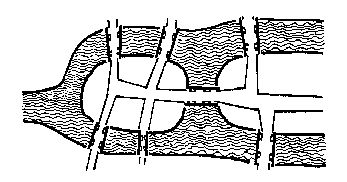
哥尼斯堡是位于普累格河上的一座城市，它包含两个岛屿及连接它们的七座桥，如下图所示。

可否走过这样的七座桥，而且每桥只走过一次？瑞士数学家欧拉(Leonhard Euler，1707—1783)最终解决了这个问题，并由此创立了拓扑学。

这个问题如今可以描述为判断欧拉回路是否存在的问题。欧拉回路是指不令笔离开纸面，可画过图中每条边仅一次，且可以回到起点的一条回路。现给定一个无向图，问是否存在欧拉回路？

输入格式:

输入第一行给出两个正整数，分别是节点数N (1)和边数M；随后的M行对应M条边，每行给出一对正整数，分别是该条边直接连通的两个节点的编号（节点从1到N编号）。

输出格式:

若欧拉回路存在则输出1，否则输出0。

输入样例1:

6 10
1 2
2 3
3 1
4 5
5 6
6 4
1 4
1 6
3 4
3 6

输出样例1:

1

输入样例2:

5 8
1 2
1 3
2 3
2 4
2 5
5 3
5 4
3 4

输出样例2:

0
题目分析：一道利用 图的遍历的题 做这道题需要知道的是 无向图存在欧拉回路的充要条件 当且仅当该图所有顶点度数为偶数，且该图是连通图

 #define _CRT_SECURE_NO_WARNINGS
 #include<stdio.h>
 #include<string.h>
 #include<malloc.h>

 typedef struct ENode* Edge;
 struct ENode
 {
     int V1, V2;
 };
 typedef struct GNode* Graph;
 struct GNode
 {
     int G[][];
     int Ne;
     int Nv;
 };

 int Degree[];
 int Collected[];
 int Flag = ;
 int IsEdge(int V1,int V2,Graph Gra)
 {
     return Gra->G[V1][V2];
 }
 void Insert(Graph Gra, Edge E)
 {
     Gra->G[E->V1][E->V2] = ;
     Gra->G[E->V2][E->V1] = ;
 }
 Graph CreateGraph(int Nv)
 {
     Graph Gra = (Graph)malloc(sizeof(struct GNode));
     Gra->Ne = ;
     Gra->Nv = Nv;
     for (int i = ; i <= Gra->Nv; i++)
         for (int j = ; j <= Gra->Nv; j++)
             Gra->G[i][j] = ;
     return Gra;
 }

 Graph BuildGraph()
 {
     int N, M;
     scanf("%d%d", &N, &M);
     Graph Gra = CreateGraph(N);
     Edge E = (Edge)malloc(sizeof(struct ENode));
     for (int i = ; i < M; i++)
     {
         scanf("%d%d", &(E->V1), &(E->V2));
         Degree[E->V1]++;
         Degree[E->V2]++;
         Insert(Gra, E);
     }
     return Gra;
 }

 void DFS(Graph Gra,int V)
 {
     for(int i=;i<=Gra->Nv;i++)
         if (!Collected[i] && IsEdge(V, i, Gra))
         {
             Collected[i] = ;
             if (Degree[i] %  == )
                 Flag = ;
             DFS(Gra, i);
         }
 }
 int IsCollected(int Nv)
 {
     for (int i = ; i <= Nv; i++)
         if (!Collected[i])
             return ;
     return ;
 }
 int main()
 {
     Graph Gra = BuildGraph();
     DFS(Gra, );
     if (Flag && IsCollected(Gra->Nv))
         printf("");
     else
         printf("");
 }