Java实现最近点问题

**问题描述：**

给定某空间中（直线空间或平面空间）n个点，请找出它们中的最近点对。你需要完成下列任务：

1、随机产生或手工输入n个点的坐标。

2、输出最近的两个点的坐标。

3、算法尽可能效率高。



解决方案：



针对问题，主要包括两个方面的问题，一是在直线空间求最近点对，二是在平面空间求最近点对。具体解决办法如下：

（1）直线空间求最近点对问题

求最近点对如果直接用蛮力法，即有n个点，从第一个点开始依次算出两点直接的距离，进行大小比较，求出最小值，其时间效率为O（n^2）。那有没有效率更高一点的办法呢？结果当然是有的，那就是采用迭代法（时间效率为O(n*logn)，先找出一组点中的中间点，使得在中间点左边的x坐标小于中间点x坐标，中间点右边的x坐标大于中间点x坐标,分成左右两组，用第一组左边组X最大值与右边组X最小值相减即得当前最短距离，在依次迭代，最后递归合并求出最终最短距离。

分治法方案具体代码如下：

package com.liuzhen.ex_two;

public class ClosestPionts {

    //初始化一个随机数组
    public static int[] initializationArray(int n){
        int[] result = new int[n];
        for(int i = 0;i < n;i++)
            result[i] = (int)(Math.random()*1000); //采用随机函数随机生成1~1000之间的数
        return result;

    }

    //返回数组中最大值
    public static int getArrayMax(int a[] , int first , int end){
        int max = a[first];
        for(int i = first;i < end;i++){
            if(max < a[i])
                max = a[i];
        }
        return max;
    }

    //返回数组中最小值
    public static int getArrayMin(int a[] , int first , int end){
        int min = a[first];
        for(int i = first;i < end;i++){
            if(min > a[i])
                min = a[i];
        }
        return min;
    }

    //交换数组a[n]中两个数的值
    public static void swapArray(int a[] , int i , int j){
        int temp = a[i];
        a[i] = a[j];
        a[j] = temp;
    }

    //采用分治法将数组a[n]分成两组,满足a[n1]<m,a[n2]>m(其中n1+n2 = n)
    public static int divideArray(int a[],int first,int end){
        int max = getArrayMax(a,first,end);
        int min = getArrayMin(a,first,end);
        double m = (max + min)/2.0;
        //System.out.println("分治法算出中位数m:"+m);
        int i = first , j = end-1;
        //int a1 = 0;
        for( ;i+1 <= j;){
            while(a[i] < m && i+1 <= j)
                i++;
            while(a[j] > m && i+1 <= j)
                j--;
        //  a1++;
        //    System.out.println("第"+a1+"此交换时a[i] = "+a[i]+" i = "+i+"  a[j] = "+a[j]+" j = "+j);
            swapArray(a,i,j);   //a[i]大于m的值与a[j]小于m的值进行交换，但数组的位置不变
        }
        //System.out.println("分组后，返回的序号j值是："+(j));
        return j;
    }

    //采用递归法合并最短距离值，返回最短距离的点
    public static int[] getMinDistancePoint(int a[] , int result[],int n ,int first , int end) {

        if(end-first <= 1){   //递归终止条件
             return result;
        }

        int j = divideArray(a,first,end);
        int minDistance = result[1] - result[0];  //最短距离两点之间的距离大小
        if(minDistance > getArrayMin(a,j,end)-getArrayMax(a,first,j))
        {
            result[0] = getArrayMax(a,first,j);   //最短距离两点中数值最小的点
            result[1] = getArrayMin(a,j,end);   //最短距离两点中数值最小的点
        }
        int result_one[] = getMinDistancePoint(a,result,2,first,j);   //递归
        int minDistance_one = result_one[1] - result_one[0];
        int result_two[] = getMinDistancePoint(a,result,2,j,end);   //递归
        int minDistance_two = result_two[1] - result_two[0];
        if(minDistance > minDistance_one)
            result = result_one;
        if(minDistance > minDistance_two)
            result = result_two;
        return result;
    }
    public static void main(String[] args){
        int a[] = new int[10];
        int b[] = new int[2];
        b[0] = 0;
        b[1] = 100;
        a = initializationArray(15);
        String one_text = "";
        for(int i = 0;i < 15;i++){
            one_text += "直线随机点Point["+i+"] = "+a[i]+"\n";
            //System.out.print("数组a["+i+"] = "+a[i]+"\n");
        }
        int result[] = getMinDistancePoint(a,b,2,0,15);
        //System.out.println("result[0] = "+result[0]+"\n"+"result[1] = "+result[1]);
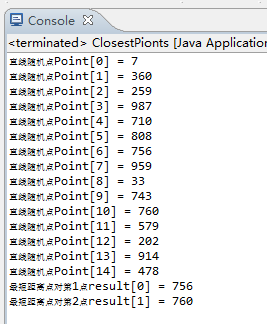
        one_text += "最短距离点对第1点result[0] = "+result[0]+"\n"+"最短距离点对第2点result[1] = "+result[1];
        System.out.print(one_text);
    }
}

结果为

（2）平面空间求最近点对问题

平面空间教直线空间求最近点对问题就变得更加复杂一点，在此就只讨论使用蛮力法求解平面空间求最近点对问题，如有对平面使用分治法求解感兴趣的同学请看本文末尾参考资料2。

蛮力法方案具体如下：

由于是在平面，点坐标表示为（x,y）,在此先创建一个Point类(方便后续功能类实现)：

package com.liuzhen.ex_two;

public class Point {

    private int x;   //平面点中的x坐标
    private int y;   //平面点中的y坐标

    //未给类对象初始化时，默认点坐标为(0,0)
    public Point(){
        this.x = 0;
        this.y = 0;
    }

    public Point(int x,int y){
        this.x = x;
        this.y = y;
    }

    //给x赋值
    public void setX(int x){
        this.x = x;
    }

    //给y赋值
    public void setY(int y){
        this.y = y;
    }

    //返回x
    public int getX(){
        return x;
    }

    //返回y
    public int getY(){
        return y;
    }
}

蛮力法

package com.liuzhen.ex_two;

public class ClosestPionts {//平面中求两点最短距离问题解法
    //初始化一个平面中n个点，具体点的坐标值随机生成
    public static Point[] initializationPlaneArray(int n){
        Point result[] = new Point[n];
        for(int i = 0;i < n;i++){
            int x1 = (int)(Math.random()*50); //采用随机函数随机生成1~100之间的数
            int y1 =  (int)(Math.random()*50);
            result[i] = new Point(x1,y1);
        }
        return result;
    }

    //蛮力法直接求平面中两点之间的最短距离，返回最短距离的两点坐标
    public static Point[] getMinDistancePlanePoint(Point a[],int n){
        Point result[] = new Point[2];
        double min = 10000;    //定义两点之间最短距离变量，初始化为10000
        for(int i = 0;i < n;i++){
            int x = a[i].getX();
            int y = a[i].getY();
            for(int j = i+1;j < n;j++){
                int x1 = a[j].getX();
                int y1 = a[j].getY();
                long minSquare = (x-x1)^2 + (y-y1)^2;   //利用数学中求两点之间距离公式，得到两点之间距离的平方
                double min1 = Math.sqrt(minSquare);    //求两点之间距离的中间变量
                if(min > min1){
                    min = min1;
                    result[0] = new Point(x,y);
                    result[1] = new Point(x1,y1);
                }
            }
        }

        return result;
    }

    public static void main(String[] args){
        String two_text = "";
        Point c[] = initializationPlaneArray(15);
        for(int i = 0;i < 15;i++){
            two_text += "Point["+i+"] = "+"("+c[i].getX()+","+c[i].getY()+")"+"\n";
            //System.out.println("c["+i+"] = "+"("+c[i].getX()+","+c[i].getY()+")");
        }
        //System.out.println(two_text);
        Point back[] = getMinDistancePlanePoint(c,15);
        for(int i = 0;i < 2;i++){
            two_text +=  "距离最短的两点第"+(i+1)+"个点坐标是："+"("+back[i].getX()+","+back[i].getY()+")"+"\n";
            //System.out.println("距离最短的两点第"+(i+1)+"个点坐标是："+"("+back[i].getX()+","+
        //back[i].getY()+")");
        }
        System.out.println(two_text);
    }

}

结果为