Tarjan算法:求解无向连通图图的割点(关节点)与桥(割边)
1. 割点与连通度
在无向连通图中,删除一个顶点v及其相连的边后,原图从一个连通分量变成了两个或多个连通分量,则称顶点v为割点,同时也称关节点(Articulation Point)。一个没有关节点的连通图称为重连通图(biconnected graph)。若在连通图上至少删去k 个顶点才能破坏图的连通性,则称此图的连通度为k。
关节点和重连通图在实际中较多应用。显然,一个表示通信网络的图的连通度越高,其系统越可靠,无论是哪一个站点出现故障或遭到外界破坏,都不影响系统的正常工作;又如,一个航空网若是重连通的,则当某条航线因天气等某种原因关闭时,旅客仍可从别的航线绕道而行;再如,若将大规模的集成电路的关键线路设计成重连通的话,则在某些元件失效的情况下,整个片子的功能不受影响,反之,在战争中,若要摧毁敌方的运输线,仅需破坏其运输网中的关节点即可。
简单的例子
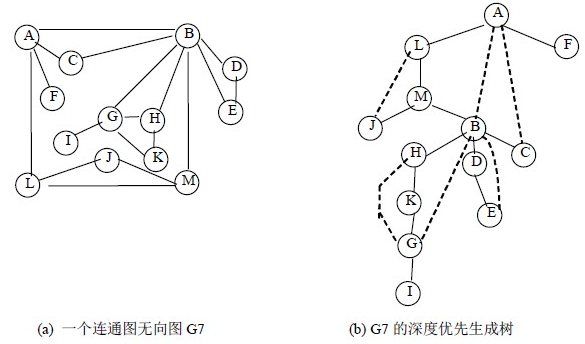
(a)中G7 是连通图,但不是重连通图。图中有三个关节点A、B 和G 。若删去顶点B 以及所有依附顶点B 的边,G7 就被分割成三个连通分量{A、C、F、L、M、J}、{G、H、I、K}和{D、E}。类似地,若删去顶点A 或G 以及所依附于它们的边,则G7 被分割成两个连通分量。
2. 求割点的方法
暴力的方法:
- 依次删除每一个节点v
- 用DFS(或BFS)判断还是否连通
- 再把节点v加入图中
若用邻接表(adjacency list),需要做V次DFS,时间复杂度为O(V∗(V+E))。(题外话:我在面试实习的时候,只想到暴力方法;面试官提示只要一次DFS就就可以找到割点,当时死活都没想出来)。
有关DFS搜索树的概念
在介绍算法之前,先介绍几个基本概念
- DFS搜索树:用DFS对图进行遍历时,按照遍历次序的不同,我们可以得到一棵DFS搜索树,如图(b)所示。
- 树边:(在[2]中称为父子边),在搜索树中的实线所示,可理解为在DFS过程中访问未访问节点时所经过的边。
- 回边:(在[2]中称为返祖边、后向边),在搜索树中的虚线所示,可理解为在DFS过程中遇到已访问节点时所经过的边。
基于DFS的算法
该算法是R.Tarjan发明的。观察DFS搜索树,我们可以发现有两类节点可以成为割点:
- 对根节点u,若其有两棵或两棵以上的子树,则该根结点u为割点;
- 对非叶子节点u(非根节点),若其子树的节点均没有指向u的祖先节点的回边,说明删除u之后,根结点与u的子树的节点不再连通;则节点u为割点。
对于根结点,显然很好处理;但是对于非叶子节点,怎么去判断有没有回边是一个值得深思的问题。
我们用dfn[u]记录节点u在DFS过程中被遍历到的次序号,low[u]记录节点u或u的子树通过非父子边追溯到最早的祖先节点(即DFS次序号最小),那么low[u]的计算过程如下:

下表给出图(a)对应的dfn与low数组值。
| i | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| vertex | A | B | C | D | E | F | G | H | I | J | K | L | M |
| dfn[i] | 1 | 5 | 12 | 10 | 11 | 13 | 8 | 6 | 9 | 4 | 7 | 2 | 3 |
| low[i] | 1 | 1 | 1 | 5 | 5 | 1 | 5 | 5 | 8 | 2 | 5 | 1 | 1 |
对于情况2,当(u,v)为树边且low[v] >= dfn[u]时,节点u才为割点。该式子的含义:以节点v为根的子树所能追溯到最早的祖先节点要么为v要么为u。
代码实现
void dfs(int u) {
//记录dfs遍历次序
static int counter = ;
//记录节点u的子树数
int children = ;
ArcNode *p = graph[u].firstArc;
visit[u] = ;
//初始化dfn与low
dfn[u] = low[u] = ++counter;
for(; p != NULL; p = p->next) {
int v = p->adjvex;
//节点v未被访问,则(u,v)为树边
if(!visit[v]) {
children++;
parent[v] = u;
dfs(v);
low[u] = min(low[u], low[v]);
//case (1)
if(parent[u] == NIL && children > ) {
printf("articulation point: %d\n", u);
}
//case (2)
if(parent[u] != NIL && low[v] >= dfn[u]) {
printf("articulation point: %d\n", u);
}
}
//节点v已访问,则(u,v)为回边
else if(v != parent[u]) {
low[u] = min(low[u], dfn[v]);
}
}
}
采用邻接表存储图,该算法的时间复杂度应与DFS相同,为O(V+E)O(V+E)。
3. 参考资料
[1] see xidian, 图的连通性—关节点和重连通分量.
[2] byvoid, 图的割点、桥与双连通分支.
[3] GeeksforGeeks, Articulation Points (or Cut Vertices) in a Graph.
仅供自己学习,原文from: https://www.cnblogs.com/en-heng/p/4002658.html
简介:
割边和割点的定义仅限于无向图中。我们可以通过定义以蛮力方式求解出无向图的所有割点和割边,但这样的求解方式效率低。Tarjan提出了一种快速求解的方式,通过一次DFS就求解出图中所有的割点和割边。
欢迎探讨,如有错误敬请指正
如需转载,请注明出处 http://www.cnblogs.com/nullzx/
1. 割点与桥(割边)的定义
在无向图中才有割边和割点的定义
割点:无向连通图中,去掉一个顶点及和它相邻的所有边,图中的连通分量数增加,则该顶点称为割点。
桥(割边):无向联通图中,去掉一条边,图中的连通分量数增加,则这条边,称为桥或者割边。
割点与桥(割边)的关系:
1)有割点不一定有桥,有桥一定存在割点
2)桥一定是割点依附的边。
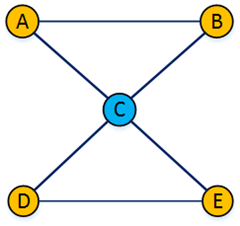
下图中顶点C为割点,但和C相连的边都不是桥。
2. 暴力解决办法解决求解割点集和割边集
暴力法的原理就是通过定义求解割点和割边。在图中去掉某个顶点,然后进行DFS遍历,如果连通分量增加,那么该顶点就是割点。如果在图中去掉某条边,然后进行DFS遍历,如果连通分量增加,那么该边就是割边。对每个顶点或者每个边进行一次上述操作,就可以求出这个图的所有割点和割边,我们称之为这个图的割点集和割边集。
在具体的代码实现中,并不需要真正删除该顶点和删除依附于该顶点所有边。对于割点,我们只需要在DFS前,将该顶点对应是否已访问的标记置为ture,然后从其它顶点为根进行DFS即可。对于割边,我们只需要禁止从这条边进行DFS后,如果联通分量增加了,那么这条边就是割边。
3. Tarjan算法的原理
判断一个顶点是不是割点除了从定义,还可以从DFS(深度优先遍历)的角度出发。我们先通过DFS定义两个概念。
假设DFS中我们从顶点U访问到了顶点V(此时顶点V还未被访问过),那么我们称顶点U为顶点V的父顶点,V为U的孩子顶点。在顶点U之前被访问过的顶点,我们就称之为U的祖先顶点。
显然如果顶点U的所有孩子顶点可以不通过父顶点U而访问到U的祖先顶点,那么说明此时去掉顶点U不影响图的连通性,U就不是割点。相反,如果顶点U至少存在一个孩子顶点,必须通过父顶点U才能访问到U的祖先顶点,那么去掉顶点U后,顶点U的祖先顶点和孩子顶点就不连通了,说明U是一个割点。
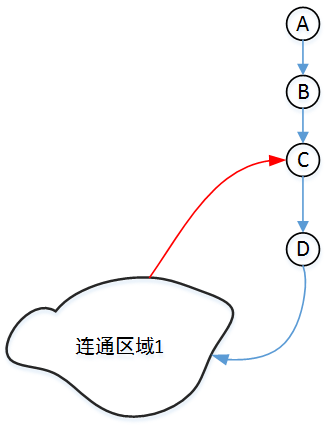
上图中的箭头表示DFS访问的顺序(而不表示有向图),对于顶点D而言,D的孩子顶点可以通过连通区域1红色的边回到D的祖先顶点C(此时C已被访问过),所以此时D不是割点。
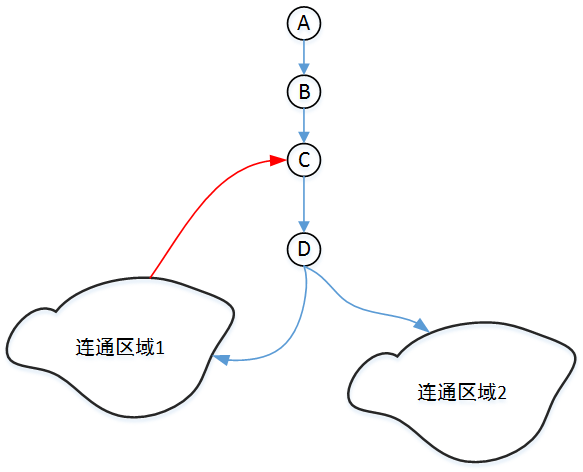
上图中的连通区域2中的顶点,必须通过D才能访问到D的祖先顶点,所以说此时D为割点。再次强调一遍,箭头仅仅表示DFS的访问顺序,而不是表示该图是有向图。
这里我们还需要考虑一个特殊情况,就是DFS的根顶点(一般情况下是编号为0的顶点),因为根顶点没有祖先顶点。其实根顶点是不是割点也很好判断,如果从根顶点出发,一次DFS就能访问到所有的顶点,那么根顶点就不是割点。反之,如果回溯到根顶点后,还有未访问过的顶点,需要在邻接顶点上再次进行DFS,根顶点就是割点。
4. Tarjan算法的实现细节
在具体实现Tarjan算法上,我们需要在DFS(深度优先遍历)中,额外定义三个数组dfn[],low[],parent[]
4.1 dfn数组
dnf数组的下标表示顶点的编号,数组中的值表示该顶点在DFS中的遍历顺序(或者说时间戳),每访问到一个未访问过的顶点,访问顺序的值(时间戳)就增加1。子顶点的dfn值一定比父顶点的dfn值大(但不一定恰好大1,比如父顶点有两个及两个以上分支的情况)。在访问一个顶点后,它的dfn的值就确定下来了,不会再改变。
4.2 low数组
low数组的下标表示顶点的编号,数组中的值表示DFS中该顶点不通过父顶点能访问到的祖先顶点中最小的顺序值(或者说时间戳)。
每个顶点初始的low值和dfn值应该一样,在DFS中,我们根据情况不断更新low的值。
假设由顶点U访问到顶点V。当从顶点V回溯到顶点U时,
如果
dfn[v] < low[u]
那么
low[u] = dfn[v]
如果顶点U还有它分支,每个分支回溯时都进行上述操作,那么顶点low[u]就表示了不通过顶点U的父节点所能访问到的最早祖先节点。
4.3 parent数组
parent[]:下标表示顶点的编号,数组中的值表示该顶点的父顶点编号,它主要用于更新low值的时候排除父顶点,当然也可以其它的办法实现相同的功能。
4.4 一个具体的例子
现在我们来看一个例子,模仿程序计算各个顶点的dfn值和low值。下图中蓝色实线箭头表示已访问过的路径,无箭头虚线表示未访问路径。已访问过的顶点用黄色标记,未访问的顶点用白色标记,DFS当前正在处理的顶点用绿色表示。带箭头的蓝色虚线表示DFS回溯时的返回路径。
1)
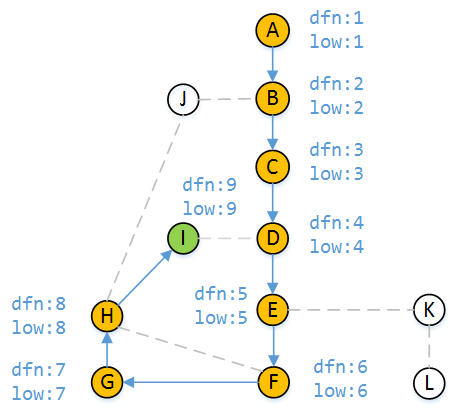
当DFS走到顶点H时,有三个分支,我们假设我们先走H-I,然后走H-F,最后走H-J。从H访问I时,顶点I未被访问过,所以I的dfn和low都为9。根据DFS的遍历顺序,我们应该从顶点I继续访问。
2)
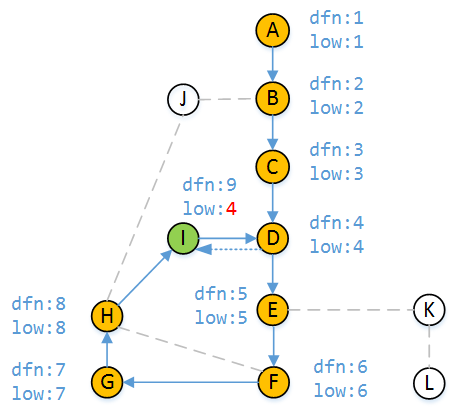
上图表示由顶点I访问顶点D,而此时发现D已被访问,当从D回溯到I时,由于
dfn[D] < dfn[I]
说明D是I的祖先顶点,所以到现在为止,顶点I不经过父顶点H能访问到的小时间戳为4。
3)
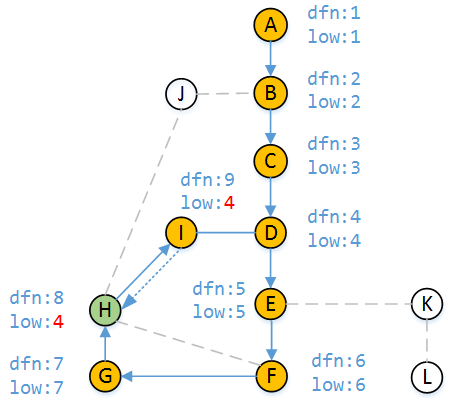
根据DFS的原理,我们从顶点I回到顶点H,显然到目前为止顶点H能访问到的最小时间戳也是4(因为我们到现在为止只知道能从H可以通过I访问到D),所以low[H] = 4
4)
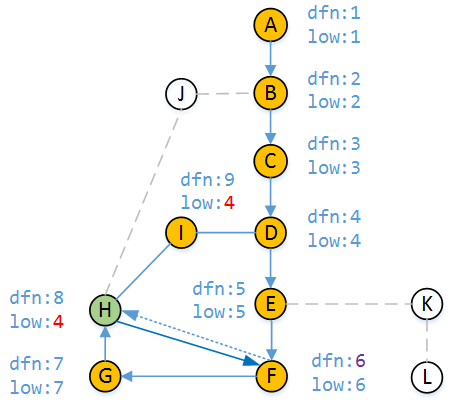
现在我们继续执行DFS,走H-F路径,发现顶点F已被访问且dfn[F] < dfn[H],说明F是H的祖先顶点,但此时顶点H能访问的最早时间戳是4,而F的时间戳是6,依据low值定义low[H]仍然为4。
5)
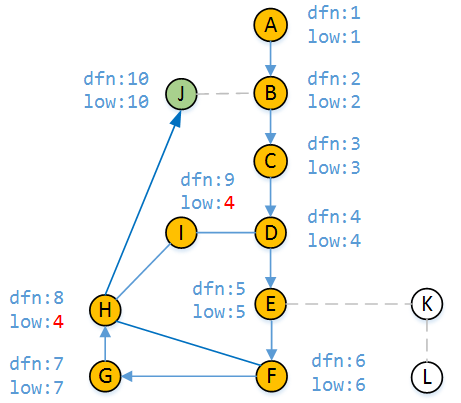
最后我们走H-J路径,顶点J未被访问过所以 dfn[J] = 10 low[J] = 10
6)
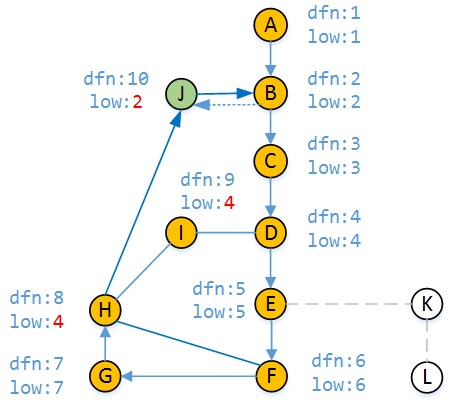
同理,由DFS访问顶点B,dfn[J] > dfn[B],B为祖先顶点,顶点J不经过父顶点H能访问到的最早时间戳就是dfn[B],即low[J] = 2
7)
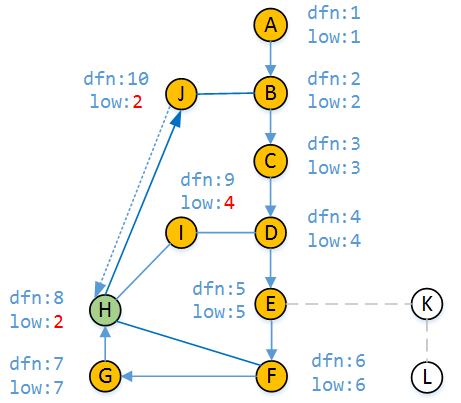
我们从顶点J回溯到顶点H,显然到目前为止顶点H能访问到的最早时间戳就更新为2(因为我们到现在为止知道了能从H访问到J),所以low[H] = 2
8)
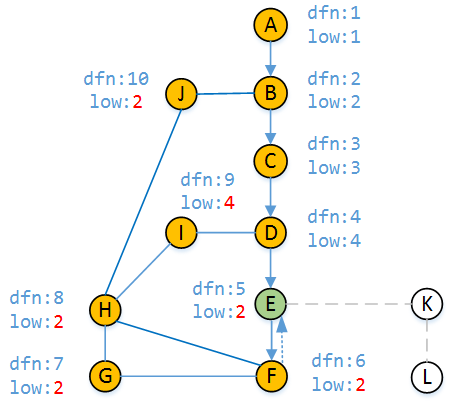
根据DFS原理,我们从H回退到顶点E(H回退到G,G回退到F,F回退到E的过程省略),所经过的顶点都会更新low值,因为这些顶点不用通过自己的父顶点就可以和顶点B相连。当回溯到顶点E时,还有未访问过的顶点,那么继续进行E-K分支的DFS。
9)
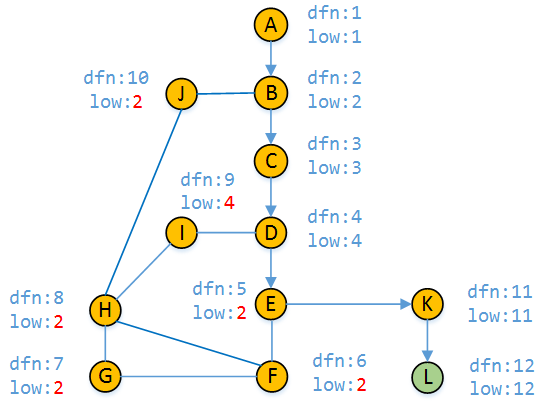
从E-K分支访问到顶点L时,顶点k和L的的dfn值和low值如图上图所示
10)
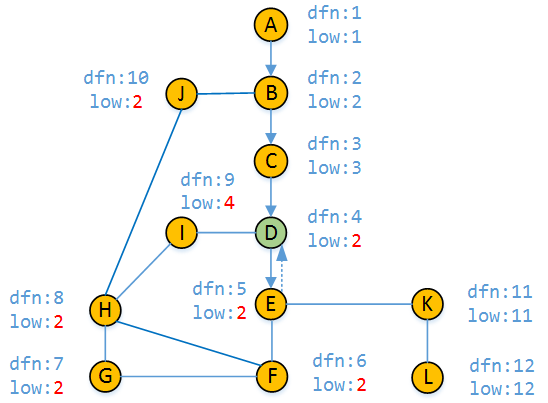
接着我们继续回溯到了顶点D(中间过程有所省略),并更新low[D]
11)
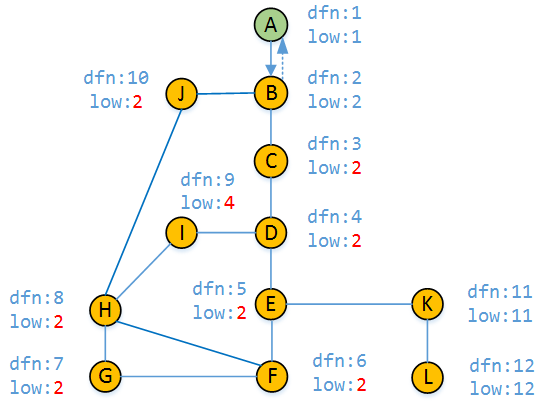
最后,按照DFS的原理,我们回退到顶点A,并且求出来了每个顶点的dfn值和low值。
4.5 割点及桥的判定方法
割点:判断顶点U是否为割点,用U顶点的dnf值和它的所有的孩子顶点的low值进行比较,如果存在至少一个孩子顶点V满足low[v] >= dnf[u],就说明顶点V访问顶点U的祖先顶点,必须通过顶点U,而不存在顶点V到顶点U祖先顶点的其它路径,所以顶点U就是一个割点。对于没有孩子顶点的顶点,显然不会是割点。
桥(割边):low[v] > dnf[u] 就说明V-U是桥
需要说明的是,Tarjan算法从图的任意顶点进行DFS都可以得出割点集和割边集。
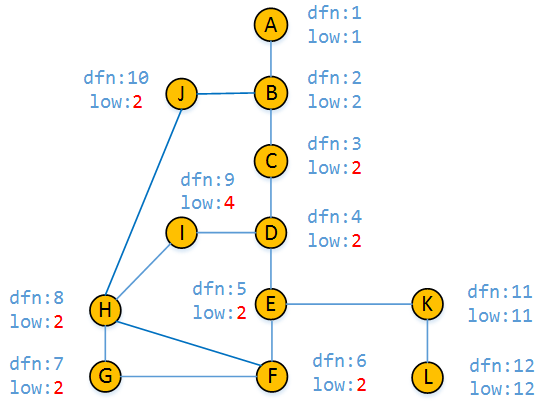
从上图的结果中我们可以看出,顶点B,顶点E和顶点K为割点,A-B以及E-K和K-L为割边。
5.代码实现:
测试:
------图的邻接表示法-------0: [0,5] [0,1] [0,2] [0,6]1: [1,0]2: [2,0]3: [3,4] [3,5]4: [4,3] [4,6] [4,5]5: [5,0] [5,4] [5,3]6: [6,4] [6,7] [6,9] [6,0]7: [7,8] [7,6]8: [8,7]9: [9,12] [9,10] [9,11] [9,6]10: [10,9]11: [11,12] [11,9]12: [12,9] [12,11]-------图中的割点-------0679-------图中的割边-----7867910690102
6. 参考内容
[1]. http://www.cnblogs.com/en-heng/p/4002658.html
[2]. http://blog.csdn.net/wtyvhreal/article/details/43530613
[3]. http://www.cppblog.com/ZAKIR/archive/2010/08/30/124869.html?opt=admin
[4].https://www.cnblogs.com/nullzx/p/7968110.html
Network(求割点)
http://poj.org/problem?id=1144
题目描述
A Telephone Line Company (TLC) is establishing a new telephone cable network. They are connecting several places numbered by integers from 1 to N. No two places have the same number. The lines are bidirectional and always connect together two places and in each place the lines end in a telephone exchange. There is one telephone exchange in each place. From each place it is possible to reach through lines every other place, however it need not be a direct connection, it can go through several exchanges. From time to time the power supply fails at a place and then the exchange does not operate. The officials from TLC realized that in such a case it can happen that besides the fact that the place with the failure is unreachable, this can also cause that some other places cannot connect to each other. In such a case we will say the place (where the failure occured) is critical. Now the officials are trying to write a program for finding the number of all such critical places. Help them
Input
The input file consists of several blocks of lines. Each block describes one network. In the first line of each block there is the number of places N < 100. Each of the next at most N lines contains the number of a place followed by the numbers of some places to which there is a direct line from this place. These at most N lines completely describe the network, i.e., each direct connection of two places in the network is contained at least in one row. All numbers in one line are separated by one space. Each block ends with a line containing just ‘0’. The last block has only one line with N = 0.
Output
The output contains for each block except the last in the input file one line containing the number of critical places.
Sample Input
Sample Output
题意翻译:
多组数据读入一个数n,n=0时退出,代表n个点的无向图。下面若干行,每行第一个数为u,u=0时退出,后面若干个数v,代表和u相连的点v,遇到换行退出。对于每组数据,输出图的割顶个数(输入较坑,所以详细说明)。
解题思路:
无向图求割点,测试模版,注意输入字符串的处理。
代码如下:
#include <stdio.h>
#include <iostream>
#include <string.h>
#include <algorithm>
#include <string>
#include <sstream>
using namespace std;
#define maxn 105 struct edge{
int v;
int next;
}Edge[maxn*maxn];//边的集合,边最多为n*(n-1),故要开点数的平方 int node[maxn];//顶点集合
int DFN[maxn];//节点u搜索的序号(时间戳)
int LOW[maxn];//u或u的子树能够追溯到的最早的栈中节点的序号(时间戳)
int n;//n:点的个数
int cnt_edge;//边的计数器
int Index;//序号(时间戳)
int fa[maxn]; //父亲编号
int GD[maxn]; //是否为割点 void add_edge(int u,int v)//邻接表存储
{
Edge[cnt_edge].next=node[u];
Edge[cnt_edge].v=v;
node[u]=cnt_edge++;
} void tarjan(int u)
{
int children=;//记录节点u的子树数
DFN[u]=LOW[u]=++Index;
for(int i=node[u];i!=-;i=Edge[i].next)
{
int v=Edge[i].v;
if(!DFN[v])//如果点v没被访问 ,则(u,v)为树边
{
children++;
fa[v]=u;
tarjan(v);
LOW[u]=min(LOW[u],LOW[v]);
if(fa[u]==&&children>&&!GD[u])
{
GD[u]=;
}
if(fa[u]&&LOW[v]>=DFN[u]&&!GD[u])
{
GD[u]=;
} }
else //如果点v已经被访问过
{
if(DFN[v])
LOW[u]=min(LOW[u],DFN[v]);
}
}
} void init()//初始化,注意不要把n初始为0
{
cnt_edge=;
Index=;
memset(Edge,,sizeof(Edge));
memset(node,-,sizeof(node));
memset(DFN,,sizeof(DFN));
memset(LOW,,sizeof(LOW));
memset(fa,,sizeof(fa));
memset(GD,,sizeof(GD));
} int main()
{
freopen("sample.txt","r",stdin);
while(~scanf("%d",&n)&&n)
{
init();
char str[];
getchar();
while(cin.getline(str,)&&str[]!='')//gets不支持,用cin.getline来代替gets
{
istringstream is(str);
int u,v;
is>>u;
while(is>>v)//while中不要写成is,要不最后一个信息会重复赋给v两次
{
add_edge(u,v);//注意是无向边
add_edge(v,u);
}
}
for(int i=;i<=n;i++)
{
if(!DFN[i])
{
tarjan(i);
}
}
int sum=;
for(int i=;i<=n;i++)
{
if(GD[i])
sum++;
}
printf("%d\n",sum);
}
return ;
}
UVA796 Critical Links —— 割边(桥)
https://vjudge.net/problem/UVA-796
题目描述
In a computer network a link L, which interconnects two servers, is considered critical if there are at least two servers A and B such that all network interconnection paths between A and B pass through L. Removing a critical link generates two disjoint sub–networks such that any two servers of a sub–network are interconnected. For example, the network shown in figure 1 has three critical links that are marked bold: 0 -1, 3 - 4 and 6 - 7.
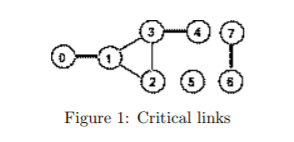
It is known that:
1. the connection links are bi–directional;
2. a server is not directly connected to itself;
3. two servers are interconnected if they are directly connected or if they are interconnected with the same server;
4. the network can have stand–alone sub–networks. Write a program that finds all critical links of a given computer network.
Input
The program reads sets of data from a text file. Each data set specifies the structure of a network and has the format: no of servers server0 (no of direct connections) connected server . . . connected server . . . serverno of servers (no of direct connections) connected server . . . connected server The first line contains a positive integer no of servers(possibly 0) which is the number of network servers. The next no of servers lines, one for each server in the network, are randomly ordered and show the way servers are connected. The line corresponding to serverk, 0 ≤ k ≤ no of servers − 1, specifies the number of direct connections of serverk and the servers which are directly connected to serverk. Servers are represented by integers from 0 to no of servers − 1.Input data are correct. The first data set from sample input below corresponds to the network in figure 1, while the second data set specifies an empty network.
Output
The result of the program is on standard output. For each data set the program prints the number of critical links and the critical links, one link per line, starting from the beginning of the line, as shown in the sample output below. The links are listed in ascending order according to their first element. The output for the data set is followed by an empty line.
Sample Input
()
()
()
()
()
()
()
()
Sample Output
critical links
-
-
- critical links
题目大意:给你n个点,m条边,问你有多少桥,并将其输出。
思路:模板题,不过这一题有格式要求,要求从小到大输出,并且每个数据后有空行。
问题和坑点:
这题一直wa,卡了我几个小时,看了好几个题解,感觉有的还没我写的好,但就是过不了,自闭了。
这题的输入输出样例应该有点问题,我把while中的 if(n==0) break;删了就能过了,但是删了就和样例输出不同了。。。。但就是AC了????
代码如下:
#include <stdio.h>
#include <iostream>
#include <string.h>
#include <algorithm>
#include <string>
#include <set>
#include <sstream>
using namespace std;
#define maxn 1010 struct edge{
int v;
int next;
}Edge[maxn*maxn];//边的集合 int node[maxn];//顶点集合
int DFN[maxn];//节点u搜索的序号(时间戳)
int LOW[maxn];//u或u的子树能够追溯到的最早的栈中节点的序号(时间戳)
int n;//n:点的个数
int cnt_edge;//边的计数器
int Index;//序号(时间戳)
int fa[maxn]; //父亲编号
set<pair<int,int> > st;
set<pair<int,int> >::iterator it; void add_edge(int u,int v)//邻接表存储
{
Edge[cnt_edge].next=node[u];
Edge[cnt_edge].v=v;
node[u]=cnt_edge++;
} void tarjan(int u)
{
DFN[u]=LOW[u]=++Index;
for(int i=node[u];i!=-;i=Edge[i].next)
{
int v=Edge[i].v;
if(!DFN[v])//如果点v没被访问 ,则(u,v)为树边
{
fa[v]=u;
tarjan(v);
LOW[u]=min(LOW[u],LOW[v]);
if(LOW[v]>DFN[u]) //判断是否为桥
{
st.insert(make_pair(min(u,v),max(u,v)));
} }
else if(v!=fa[u]) //如果点v已经被访问过
{
if(DFN[v])
LOW[u]=min(LOW[u],DFN[v]);
}
}
} void init()//初始化,注意不要把n初始为0
{
cnt_edge=;
Index=;
memset(Edge,,sizeof(Edge));
memset(node,-,sizeof(node));
memset(DFN,,sizeof(DFN));
memset(LOW,,sizeof(LOW));
memset(fa,,sizeof(fa));
st.clear();
} int main()
{
freopen("sample.txt","r",stdin);
while(~scanf("%d",&n))
{
init();
int u,m;
for(int i=;i<n;i++)
{
scanf("%d (%d)",&u,&m);
for(int j=;j<m;j++)
{
int v;
scanf("%d",&v);
if(v<=u)
continue;
add_edge(u,v);
add_edge(v,u);
}
}
for(int i=;i<n;i++)
{
if(!DFN[i])
{
tarjan(i);
}
}
printf("%d critical links\n",st.size());
for(it=st.begin();it!=st.end();it++)
{
printf("%d - %d\n",it->first,it->second);
}
printf("\n");
// if(n==0) //删了就能过
// break;
}
return ;
}
Tarjan算法:求解无向连通图图的割点(关节点)与桥(割边)的更多相关文章
- Tarjan算法求解无向连通图的割点、割边、点双连通分量和边双连通分量的模板
历时好几天,终于完工了! 支持无向图四种功能:1.割点的求解 2.割边的求解 3.点双连通分量的求解 4.边双连通分量的求解 全部支持重边!!!!全部支持重边!!!!全部支持重边!!!! 测试数据: ...
- TarJan 算法求解有向连通图强连通分量
[有向图强连通分量] 在有向图G中,如果两个 顶点间至少存在一条路径,称两个顶点强连通(strongly connected).如果有向图G的每两个顶点都强连通,称G是一个强连通图.非强连通图有向图的 ...
- tarjan算法--求解无向图的割点和桥
1.桥:是存在于无向图中的这样的一条边,如果去掉这一条边,那么整张无向图会分为两部分,这样的一条边称为桥 也就是说 无向连通图中,如果删除某边后,图变成不连通,则称该边为桥 2.割点:无向连通图中,如 ...
- Tarjan算法求解桥和边双连通分量(附POJ 3352 Road Construction解题报告)
http://blog.csdn.net/geniusluzh/article/details/6619575 在说Tarjan算法解决桥和边双连通分量问题之前我们先来回顾一下Tarjan算法是如何 ...
- 20行代码实现,使用Tarjan算法求解强连通分量
今天是算法数据结构专题的第36篇文章,我们一起来继续聊聊强连通分量分解的算法. 在上一篇文章当中我们分享了强连通分量分解的一个经典算法Kosaraju算法,它的核心原理是通过将图翻转,以及两次递归来实 ...
- 有向图强连通分支的Tarjan算法讲解 + HDU 1269 连通图 Tarjan 结题报告
题目很简单就拿着这道题简单说说 有向图强连通分支的Tarjan算法 有向图强连通分支的Tarjan算法伪代码如下:void Tarjan(u) {dfn[u]=low[u]=++index//进行DF ...
- Tarjan算法:求解图的割点与桥(割边)
简介: 割边和割点的定义仅限于无向图中.我们可以通过定义以蛮力方式求解出无向图的所有割点和割边,但这样的求解方式效率低.Tarjan提出了一种快速求解的方式,通过一次DFS就求解出图中所有的割点和割边 ...
- 图之强连通--Tarjan算法
强连通分量 简介 在阅读下列内容之前,请务必了解图论基础部分. 强连通的定义是:有向图 G 强连通是指,G 中任意两个结点连通. 强连通分量(Strongly Connected Components ...
- 『Tarjan算法 无向图的双联通分量』
无向图的双连通分量 定义:若一张无向连通图不存在割点,则称它为"点双连通图".若一张无向连通图不存在割边,则称它为"边双连通图". 无向图图的极大点双连通子图被 ...
随机推荐
- Oracle:文字与字符串不匹配
执行方法的时候,方法在本地跑是正常,到测试环境报错,错误代码为 ADD_MONTHS(to_date(nvl(T2.EXEC_TIME,t1.DISTRIBUTE_TIME+1),'yyyy-mm-d ...
- 【LeetCode】搜索旋转排序数组
[问题]假设按照升序排序的数组在预先未知的某个点上进行了旋转. ( 例如,数组 [0,1,2,4,5,6,7] 可能变为 [4,5,6,7,0,1,2] ). 搜索一个给定的目标值,如果数组中存在这个 ...
- Canvas绘制水波进度加载
效果: 用到图片下载: 自定义View: package com.czm.mysinkingview; import android.content.Context; import android.g ...
- python 的第一个界面程序(PyQt5)
这里用到了python的一个第三qt库PyQt5,API与qt几乎完全一样(科学严谨下...) from PyQt5.QtWidgets import QApplication, QMainWindo ...
- Flink并行度
并行执行 本节介绍如何在Flink中配置程序的并行执行.FLink程序由多个任务(转换/操作符.数据源和sinks)组成.任务被分成多个并行实例来执行,每个并行实例处理任务的输入数据的子集.任务的并行 ...
- Invalid bean definition with name 'dataSource' defined in class path resource [applicationContext.xml]
启动tomcat,访问一个web项目失败,查看日志,发现异常信息: 18-Jul-2019 15:22:16.822 严重 [main] org.apache.catalina.core.Standa ...
- (递归)P1192 台阶问题
题解: 这其实是变相的斐波那契,观察下列等式: //k=2 : 1 2 3 5 8 13 21 34...... //k=3 : 1 2 4 7 13 24 44 81... //k=4 : 1 2 ...
- ArchLinux安装(BIOS)
ArchLinux安装(BIOS) 说在前头:在经历过无数次的失败尝试过后总结出的可用的安装过程(比官方的简单一点) 官方安装指导 一.连接网络 1.连接 # wifi-menu 2.检查是否联通 ( ...
- 微信小程序返回页面传值
一.通过url传递参数,但由于navigateTo无法跳转到导航页,所以无法往导航页传递参数 wx.navigateTo({ url: 'test?id=1' }) 二.通过wx.navigateBa ...
- 谷歌 notification 测试 页面
<button onclick="notifyMe('master wei','http://cdn.sstatic.net/stackexchange/img/logos/so/so ...
