OpenCV-Python 理解SVM

目标

在这一章中

我们将对SVM有一个直观的了解

理论

线性可分数据

考虑下面的图像，它具有两种数据类型，红色和蓝色。在kNN中，对于测试数据，我们用来测量其与所有训练样本的距离，并以最小的距离作为样本。测量所有距离都需要花费大量时间，并且需要大量内存来存储所有训练样本。但是考虑到图像中给出的数据，我们是否需要那么多？

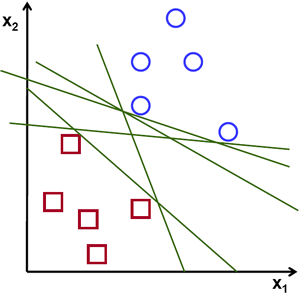
考虑另一个想法。我们找到一条线$f(x)=ax_1 + bx_2+c$，它将两条数据都分为两个区域。当我们得到一个新的test_data $X$时，只需将其替换为$f(x)$即可。如果$f(X)> 0$，则属于蓝色组，否则属于红色组。我们可以将此行称为“决策边界”。它非常简单且内存高效。可以将这些数据用直线（或高维超平面）一分为二的数据称为线性可分离数据。

因此，在上图中，你可以看到很多这样的行都是可能的。我们会选哪一个？非常直观地，我们可以说直线应该从所有点尽可能远地经过。为什么？因为传入的数据中可能会有噪音。此数据不应影响分类准确性。因此，走最远的分离线将提供更大的抗干扰能力。因此，SVM要做的是找到到训练样本的最小距离最大的直线（或超平面）。请参阅下面图像中穿过中心的粗线。

因此，要找到此决策边界，你需要训练数据。那么需要全部吗？并不用。仅接近相反组的那些就足够了。在我们的图像中，它们是一个蓝色填充的圆圈和两个红色填充的正方形。我们可以称其为支撑向量，通过它们的线称为支撑平面。它们足以找到我们的决策边界。我们不必担心所有数据。它有助于减少数据量。

接下来，找到了最能代表数据的前两个超平面。例如，蓝色数据由$w^Tx+b_0>-1$表示，红色数据由$wTx+b_0<-1$表示，其中$w$是权重向量($w=[w_1,w_2,...,w_n]$)，$x$是特征向量($x =[x_1,x_2,...,x_n]$)。$b_0$是偏置。权重矢量确定决策边界的方向，而偏置点确定其位置。现在，将决策边界定义为这些超平面之间的中间，因此表示为$w^Tx + b_0 = 0$。从支持向量到决策边界的最小距离由$distance_{support vectors}=\frac{1}{\|w\|}$给出。间隔是此距离的两倍，因此我们需要最大化此间隔。也就是说，我们需要使用一些约束来最小化新函数$L(w,b_0)$，这些约束可以表示如下：

\[\min_{w, b_0} L(w, b_0) = \frac{1}{2}||w||^2 \; \text{subject to} \; t_i(w^Tx+b_0) \geq 1 \; \forall i
\]

其中$t_i$是每类的标签，$t_i\in[-1,1]$.

非线性可分数据

考虑一些不能用直线分成两部分的数据。例如，考虑一维数据，其中'X'位于-3和+3，而'O'位于-1和+1。显然，它不是线性可分离的。但是有解决这些问题的方法。如果我们可以使用函数$f(x)=x^2$映射此数据集，则在线性可分离的9处获得'X'，在1处获得'O'。

否则，我们可以将此一维数据转换为二维数据。我们可以使用$f(x)=(x,x^2)$函数来映射此数据。然后，'X'变成(-3,9)和(3,9)，而'O'变成(-1,1)和(1,1)。这也是线性可分的。简而言之，低维空间中的非线性可分离数据更有可能在高维空间中变为线性可分离。

通常，可以将d维空间中的点映射到某个D维空间$(D> d)$，以检查线性可分离性的可能性。有一个想法可以通过在低维输入（特征）空间中执行计算来帮助在高维（内核）空间中计算点积。我们可以用下面的例子来说明。

考虑二维空间中的两个点，$p=(p_1,p_2)$和$q=(q_1,q_2)$。令$ϕ$为映射函数，它将二维点映射到三维空间，如下所示：

\[ϕ(p)=(p^2_1,p^2_2,\sqrt{2}p_1p_2)ϕ(q)=(q^2_1,q^2_2,\sqrt{2}q_1q_2)$$让我们定义一个核函数$K(p,q)$，该函数在两点之间做一个点积，如下所示：

\begin{aligned} K(p,q) = \phi(p).\phi(q) &= \phi(p)^T \phi(q) \ &= (p_{1}^2,p_{2}2,\sqrt{2} p_1 p_2).(q_{1}^2,q_{2}2,\sqrt{2} q_1 q_2) \ &= p_1 q_1 + p_2 q_2 + 2 p_1 q_1 p_2 q_2 \ &= (p_1 q_1 + p_2 q_2)^2 \ \phi(p).\phi(q) &= (p.q)^2 \end{aligned}

\[
这意味着，可以使用二维空间中的平方点积来实现三维空间中的点积。这可以应用于更高维度的空间。因此，我们可以从较低尺寸本身计算较高尺寸的特征。一旦将它们映射，我们将获得更高的空间。

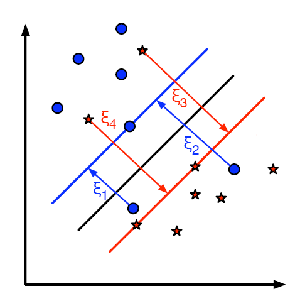
除了所有这些概念之外，还存在分类错误的问题。因此，仅找到具有最大间隔的决策边界是不够的。我们还需要考虑分类错误的问题。有时，可能会找到间隔较少但分类错误减少的决策边界。无论如何，我们需要修改我们的模型，以便它可以找到具有最大间隔但分类错误较少的决策边界。最小化标准修改为：$\min \|w\|^2+C$（分类错误的样本到其正确区域的距离）下图显示了此概念。对于训练数据的每个样本，定义一个新的参数$ξ_i$。它是从其相应的训练样本到其正确决策区域的距离。对于那些未分类错误的样本，它们落在相应的支撑平面上，因此它们的距离为零。

![](http://qiniu.aihubs.net/svm_basics3.png)

因此，新的优化函数为：
$$\min_{w, b_{0}} L(w,b_0) = ||w||^{2} + C \sum_{i} {\xi_{i}} \text{ subject to } y_{i}(w^{T} x_{i} + b_{0}) \geq 1 - \xi_{i} \text{ and } \xi_{i} \geq 0 \text{ } \forall i\]

如何选择参数C？显然，这个问题的答案取决于训练数据的分布方式。尽管没有一般性的答案，但考虑以下规则是很有用的：

C的值越大，解决方案的分类错误越少，但宽度也越小。考虑到在这种情况下，进行错误分类错误是昂贵的。由于优化的目的是最小化参数，因此几乎没有误分类的错误。
C的值越小，解决方案的宽度就越大，分类误差也越大。在这种情况下，最小化对总和项的考虑不多，因此它更多地集中在寻找具有大间隔的超平面上。

附加资源

NPTEL notes on Statistical Pattern Recognition, Chapters 25-29.

练习