[讲解]网络流最大流dinic算法

网络流最大流算法dinic

ps：本文章不适合萌新，我写这个主要是为了复习一些细节，概念介绍比较模糊，建议多刷题去理解

例题：codevs草地排水，方格取数

【抒情一下】

虽然老师说这个多半不考，但是学了没坏处，所以我就把这算法学了（准确说是补起了QAQ）

以前一直觉得dinic的代码好长好难啊，然后就知难而退

最近学了很多和看了很多以后，咱们就学会了知男♂而上了，所以我果断的回来上dinic了

【dinic】

Dinic算法是用来做最大流一类题的，代码有一丢丢的长，但其实说白了就是一个bfs+dfs就没了，所以没必要有啥心理负担

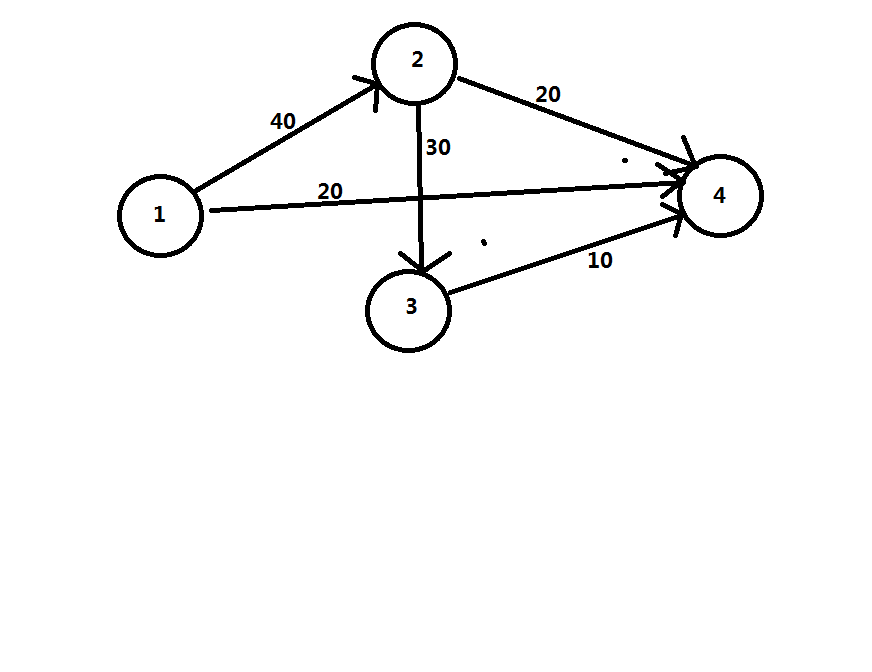
我们先来画一个图，我们需要从1点流到n点

首先看这个图，每条边上标的是这条边的容量

Dinic的想法就是对当前图去找一条还能够从s通往t的可行路

然后可行路可以由图中的边组成，也可以用图中的边的逆向边组成

至于为什么要建立逆向边和逆向边的含义，我们重新画一张图

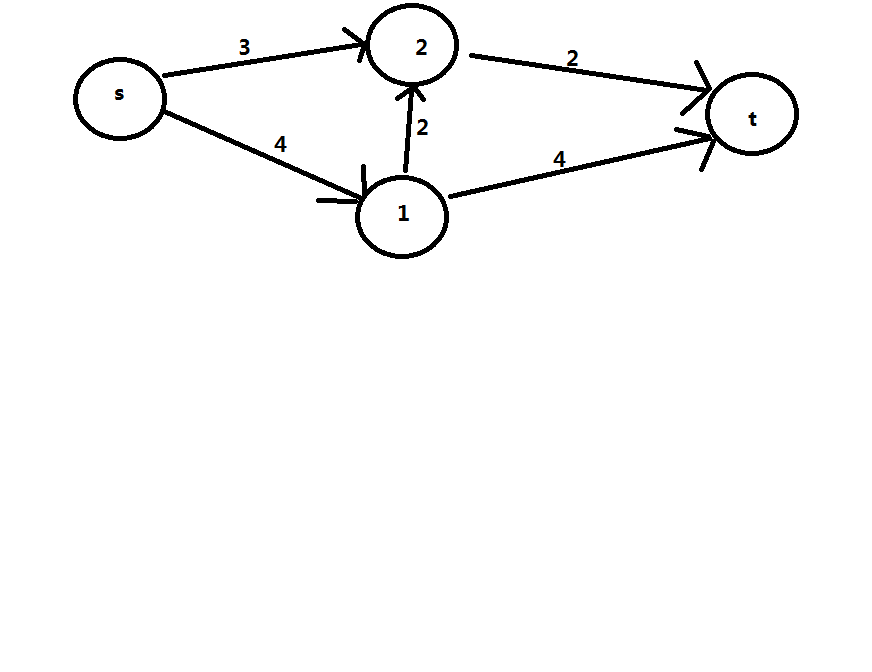
我假设这张图的目前的流量为

E(s,2)=0,E(s,1)=4,E(1,2)=2,E(2,t)=2,E(1,t)=2;

然后我们建立逆向边或者说是反向弧，就是沿着箭头的反方向建边，反向边的容量为正向边的流量（不是容量）

所以当前反向边的容量为

E(2,s)=0,E(1,s)=4,E(2,1)=2,E(t,2)=2,E(t,1)=2;

然后为什么要建立这些边，我们先看图，当前的图肯定不是最优的，这时候就要找增广路

增广路简单一点理解就是还有一条从s到t的路

然后我们发现边s,1是满的，所以找到可以流的边s,2的流量是0，然后到2点发现2,1边的容量是2（因为E(1,2)=2,所以反向此时的容量为2），最后发现1,t边容量4流量2，于是找到一条增广路

S->2->1->t，这条增广路可以扩大2的流量，所以最大流+2，为6

至于程序也很简单，首先是建图，建完图以后一个while循环（用bfs判断），bfs的过程是找还有没有增广路，然后在循环内dfs，dfs是找这条增广路的可以扩大的最大流量

至于在dfs判断是否是我们找出的合法路径，可以在bfs是对路径加深度，如果容量大于流量并且不是同一深度，那么dfs就可以继续搜索下去

然后我给一个dinic的模版，模板题就用草地排水了

 #include<cstdio>
 #include<cstring>
 #include<algorithm>
 #include<iostream>
 #include<queue>
 #include<cmath>
 #include<cstdlib>
 #include<stack>
 #define maxn 505
 using namespace std;

 queue<int>q;
 int c[maxn],head[maxn],f[maxn],n,m,dep[maxn],ans;
 struct edge{
     int u,v,w,nxt,flow;
 }e[maxn];

 int read(){
     int xx=,ff=;char ch=getchar();
     while(ch<''||ch>''){if(ch=='-')ff=-;ch=getchar();}
     while(ch>=''&&ch<=''){xx=xx*+ch-'';ch=getchar();}
     return xx*ff;
 }

 int tot=;
 void adde(int u,int v,int w){
     e[++tot].u=u;
     c[tot]=w;
     e[tot].v=v;e[tot].w=w;
     e[tot].nxt=head[u];
     head[u]=tot;
 }

 int bfs(){
     q.push();
     memset(dep,-,sizeof(dep));
     dep[]=;
     while(!q.empty()){
         int u=q.front();q.pop();
         for(int i=head[u];i!=-;i=e[i].nxt){
             int v=e[i].v;
             if(dep[v]==-&&c[i]-f[i]){
                 dep[v]=dep[u]+;
                 q.push(v);
             }
         }
     }
     if(dep[n]==-)return ;
     else return ;
 }

 int dfs(int u,int lim){
     if(u==n){ans+=lim;return lim;}
     int t;
     for(int i=head[u];i!=-;i=e[i].nxt ){
         int v=e[i].v;
         if(c[i]-f[i]&&dep[u]+==dep[v]&&(t=dfs(v,min(lim,c[i]-f[i])))){
             f[i]+=t;f[i^]-=t;return t;
         }
     }
     return ;
 }

 int main(){
     memset(head,-,sizeof(head));
     m=read();n=read();
     for(int i=;i<=m;i++){
         int u,v,w;
         u=read();v=read();w=read();
         adde(u,v,w);adde(v,u,);
     }
     while(bfs()){
         dfs(,0x3f3f3f);
     }
     printf("%d",ans);
 }

【总结】

网络流的难点在于建图，这个另类的建图可以参加一下方格取数，拓宽一下视野