UVA 12171 Sculpture

https://vjudge.net/problem/UVA-12171

题目

某人设计雕塑，用的是很扯的方法：把一堆长方体拼起来。给出长方体的坐标和长宽高，求外表面积。因为要将这雕塑进行酸洗，需要知道$V_排$

输入长方体信息，输出外表面积和$V_排$

\[0\le 每个维度的坐标值\le 500\]

\[0\le长、宽、高 \le500\]

（不会描述了）

题解

有了紫书上的提示，还是写了两个小时……

离散化+bfs

将长方体出现的坐标都存入数组，然后排序，然后使用 unique 函数， unique 函数的返回值是指向末尾哨兵的迭代器(?)，减去 begin 就可以得到剩下元素个数。

unique复杂度$O(数组原来元素个数)$，如果没有排序，那么 unique函数就没有效果（只会把与上一个元素相同的元素无视，把后面的元素移动到前面（覆盖），而不是像紫书那样说的重复元素移动到后面）

https://en.cppreference.com/w/cpp/algorithm/unique

将雕塑放进长宽高都大于500的容器里面，然后灌水，容器的体积减去水的体积就是$V_排$，水的内表面积就是雕塑的外表面积

如果水碰到了雕塑，那么就计算表面积……

三维也可以离散化，画个图可以看出来

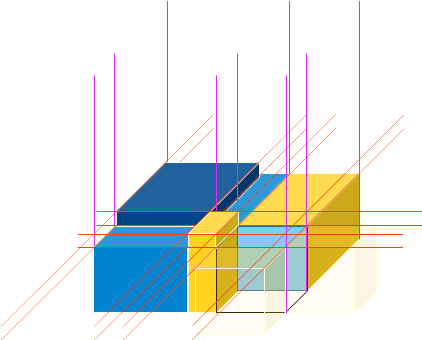
有个技巧是用左上角的坐标来代表长方体

计算面积的时候可以选择无视某条边

调试的时候可以使用文件输入……最好一开始先用简单的数据

BIG小于1000会WA……

（不想解释了= =）

AC代码：

#include<bits/stdc++.h>
using namespace std;
#define REP(i,x,y) for(register int i=(x); i<(y); i++)
#define REPE(i,x,y) for(register int i=(x); i<=(y); i++)
#ifdef sahdsg
#define DBG(a,...) printf(a, ##__VA_ARGS__)
#else
#define DBG(a,...) (void)0
#endif
#define BIG 1008
template <class T>
inline void read(T& x) {
    char c=getchar();int f=1;x=0;
    while(!isdigit(c)&&c!='-')c=getchar();if(c=='-')f=-1,c=getchar();
    while(isdigit(c)){x=x*10+c-'0';c=getchar();}x*=f;
}

struct _b {
	int x_0, y_0, z_0;
	int x_1, y_1, z_1;
} b[51];
int x[108], y[108], z[108];
int nx    , ny    , nz;
int cube[108][108][108];
int ans1=0, ans2=0;
struct node {
	int x,y,z;
};
const int dx[] = { 0, 0,-1, 0, 0, 1};
const int dy[] = { 0,-1, 0, 0, 1, 0};
const int dz[] = {-1, 0, 0, 1, 0, 0};
void getans() {
	ans1=0, ans2=BIG*BIG*BIG;
	queue<node> q;
	q.push((node){0,0,0});
	cube[0][0][0]=2;
	int delx=x[1]-x[0];
	int dely=y[1]-y[0];
	int delz=z[1]-z[0];
	ans2-=delx*dely*delz;
	while(!q.empty()) {
		node now = q.front(); q.pop();
		REP(i,0,6) {
			int newx = now.x+dx[i], newy = now.y+dy[i], newz = now.z+dz[i];
			if(newx<nx-1 && newx>=0)
			if(newy<ny-1 && newy>=0)
			if(newz<nz-1 && newz>=0) {
				if(cube[newx][newy][newz]==0) {
					q.push((node){newx,newy,newz});
					cube[newx][newy][newz]=2;
					int delx=x[newx+1]-x[newx];
					int dely=y[newy+1]-y[newy];
					int delz=z[newz+1]-z[newz];
//					DBG("```%d %d %d\n", delx, dely, delz);
					ans2-=delx*dely*delz;
				} else if(cube[newx][newy][newz]==1) {
					int delx=dx[i]?1:(x[newx+1]-x[newx]);
					int dely=dy[i]?1:(y[newy+1]-y[newy]);
					int delz=dz[i]?1:(z[newz+1]-z[newz]);
					ans1+=delx*dely*delz;

				}
			}
		}
	}
}
int main() {
	#ifdef sahdsg
	freopen("in.txt","r",stdin);
	#endif
	int T; scanf("%d", &T);
	while(0<T--) {
		int n; scanf("%d", &n);
		REP(i,0,n) {
			read(b[i].x_0);	read(b[i].y_0);	read(b[i].z_0);
			read(b[i].x_1);	read(b[i].y_1);	read(b[i].z_1);

			b[i].x_1+=b[i].x_0;
			b[i].y_1+=b[i].y_0;
			b[i].z_1+=b[i].z_0;
			#define op(k) k[i*2]=b[i].k##_0; k[i*2+1]=b[i].k##_1;
			op(x);op(y);op(z);
			#undef op

		}
		x[2*n]=BIG-1;y[2*n]=BIG-1;z[2*n]=BIG-1;
		x[2*n+1]=-1;y[2*n+1]=-1;z[2*n+1]=-1;
		sort(x,x+2*n+2); sort(y,y+2*n+2); sort(z,z+2*n+2);
		nx = unique(x,x+2*n+2)-x;
		ny = unique(y,y+2*n+2)-y;
		nz = unique(z,z+2*n+2)-z;
		memset(cube,0,sizeof cube);
//		REP(i,0,nx) REP(j,0,ny) REP(k,0,nz) DBG("```%d\t%d\t%d\n", x[i], y[j], z[k]);
		REP(i,0,n) {
			#define op(k) \
				b[i].k##_0=lower_bound(k, k+n##k, b[i].k##_0)-k;\
				b[i].k##_1=lower_bound(k, k+n##k, b[i].k##_1)-k;
			op(x);op(y);op(z);
			#undef op
//			DBG("%d\t%d\n%d\t%d\n%d\t%d\n", b[i].x_0,b[i].x_1,b[i].y_0,b[i].y_1,b[i].z_0,b[i].z_1);
			REP(qx,b[i].x_0,b[i].x_1) REP(qy,b[i].y_0,b[i].y_1) REP(qz,b[i].z_0,b[i].z_1) {
				cube[qx][qy][qz]=1;
			}
		}
		getans();
		printf("%d %d\n", ans1, ans2);

	}
	return 0;
}