C# 算法之选择排序

1、简介

选择排序是排序中比较简单的一种,实现的大致思路如下:首先我们拿到一个需要排序的数组,假设该数组的第一个元素是最小的,然后将数组中剩下的元素,于最小的元素进行比较,如果中间有比第一个元素的小的,那么设当前元素为最小的,然后剩下的元素在和当前元素进行比较,直到找到最小的.这时候第一轮循环结束,我们可以找到当前数组中最小的那个元素,在和第一个元素交换位置.第二轮循环开始,这个时候我们以及确定第一个元素是最小的,所以这轮循环第一个元素将不参与运算.这轮循环,假设第一个元素是最小的,剩下的步骤和第一轮一样.

2、C#实现

代码如下:

    /// <summary>
    /// 选择排序
    /// </summary>
    public class SelectctionSort
    {
        static void Main(string[] args)
        {
            var arr = new IComparable[] { ,,,,,, };
            var result= Sorted(arr);
            Array.ForEach(arr, Console.WriteLine);
            Console.WriteLine("排序是否成功?{0}", IsSorted(result) ? "是" : "否");
            Console.ReadKey();
        }

        /// <summary>
        /// 选择排序Main方法
        /// </summary>
        /// <param name="array"></param>
        /// <returns></returns>
        public static IComparable[] Sorted(IComparable[] array)
        {
            int count = array.Length;
            for (int i = ; i < count; i++)
            {
                //假设每一轮外循环的第一个是最小的
                int min = i;
                for (int j = i + ; j < count; j++)
                    if (Less(array[j], array[min])) min = j;
                Exchange(array, i, min);
            }
            return array;
        }

        /// <summary>
        /// 判断两个元素的大小
        /// </summary>
        /// <param name="a"></param>
        /// <param name="b"></param>
        /// <returns></returns>
        private static bool Less(IComparable a, IComparable b)
        {
            var res = a.CompareTo(b);
            return res < ;
        }

        /// <summary>
        /// 交换一轮循环后的结果
        /// </summary>
        /// <param name="array"></param>
        /// <param name="i"></param>
        /// <param name="min"></param>
        private static void Exchange(IComparable[] array,int i,int min)
        {
            var temp = array[i];
            array[i] = array[min];
            array[min] = temp;
        }

        /// <summary>
        /// 判断排序是否正确
        /// </summary>
        /// <param name="array"></param>
        /// <returns></returns>
        private static bool IsSorted(IComparable[] array)
        {
            for (int i = ; i < array.Length; i++)
            {
                if (Less(array[i], array[i-])) return false;
            }
            return true;
        }
    }

总结:内循环,负责找出这轮循环中最小的元素,外循环负责将内循环最小的元素与本轮循环中第一个元素进行交换位置,并确保下一轮外循环第i(外循环的当前索引)小的元素不参与下一轮的比较.流程图大致如下:

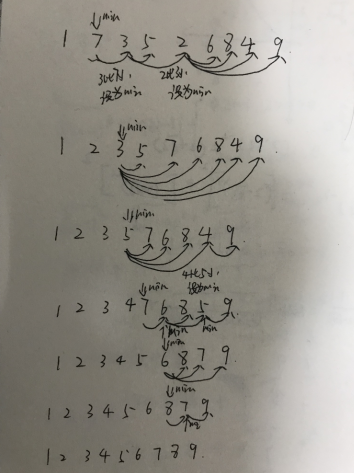
每一轮外循环i(假设有i个元素)都推举出第i小的元素,将它和第一个元素交换位置,直到所有的元素排序完毕!

重点:

通过代码和图可以推算出选择排序一共会进行N次交换(哪怕数组是有序的,通过观察代码可以发现),一共会进行(N-1)+(N-2)+(N-3)+.....+2+1(标准的等差数列,计算方式自行百度)等于N^2/2次比较.

优缺点分析:

移动数据很少,成线性关系即y(交换次数)=x(数组长度)

比较次数过多,成指数关系,随着元素的个数增多,开销指数级增大 y(比较次数)=n(数组长度)^2/2

所以,数组元素过多时,不建议使用.