python3实现二叉树的遍历与递归算法解析

1、二叉树的三种遍历方式

　　二叉树有三种遍历方式：先序遍历，中序遍历，后续遍历  即：先中后指的是访问根节点的顺序   eg:先序 根左右   中序 左根右  后序  左右根

　　遍历总体思路：将树分成最小的子树，然后按照顺序输出

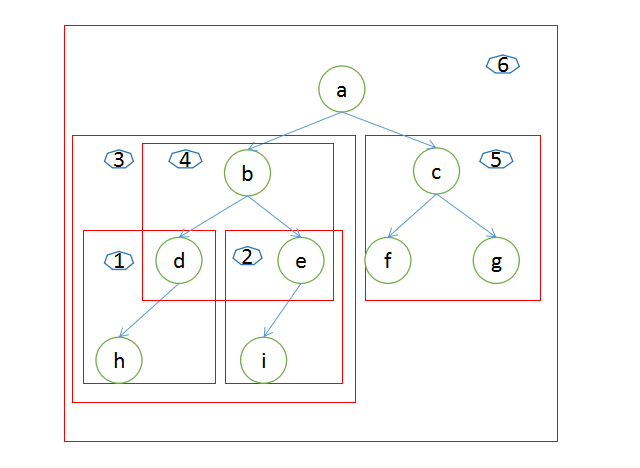
　　1.1 先序遍历

　　　　a 先访问根节点

　　　　b 访问左节点

　　　　c 访问右节点

　　　　a（b ( d ( h ) )( e ( i ) )）( c ( f )( g ))      --   abdheicfg  

　　1.2 中序遍历

　　　　a 先访问左节点

　　　　b 访问根节点

　　　　c 访问右节点

　　　　( ( ( h ) d ) b ( ( i ) e ) ) a ( ( f ) c ( g ) )  -- hdbieafcg

　　1.3后序遍历

　　　　a 先访问左节点

　　　　b 访问右节点

　　　　c 访问根节点

　　　　((hd)(ie)b)(fgc)a  -- hdiebfgca

2、python3实现树结构

#实现树结构的类，树的节点有三个私有属性  左指针 右指针 自身的值
class Node():

    def __init__(self,data=None):
        self._data = data
        self._left = None
        self._right = None

    def set_data(self,data):
        self._data = data

    def get_data(self):
        return self._data

    def set_left(self,node):
        self._left = node

    def get_left(self):
        return self._left

    def set_right(self,node):
        self._right = node

    def get_right(self):
        return self._right

if __name__ == '__main__':
    #实例化根节点
    root_node = Node('a')
    # root_node.set_data('a')
    #实例化左子节点
    left_node = Node('b')
    #实例化右子节点
    right_node = Node('c')

    #给根节点的左指针赋值，使其指向左子节点
    root_node.set_left(left_node)
    #给根节点的右指针赋值，使其指向右子节点
    root_node.set_right(right_node)

    print(root_node.get_data(),root_node.get_left().get_data(),root_node.get_right().get_data())

3、实现树的递归遍历（前 中 后 层次遍历）

下例是树的遍历算法，其中对树的类进行了优化，

#实现树结构的类，树的节点有三个私有属性  左指针 右指针 自己的值
class Node():

    def __init__(self,data =None,left=None,right = None):
        self._data = data
        self._left = left
        self._right = right

#先序遍历  遍历过程 根左右
def pro_order(tree):
    if tree == None:
        return False
    print(tree._data)
    pro_order(tree._left)
    pro_order(tree._right)

#后序遍历
def pos_order(tree):
    if tree == None:
        return False
    # print(tree.get_data())
    pos_order(tree._left)
    pos_order(tree._right)
    print(tree._data)

#中序遍历
def mid_order(tree):
    if tree == None:
        return False
    # print(tree.get_data())
    mid_order(tree._left)
    print(tree._data)
    mid_order(tree._right)

#层次遍历
def row_order(tree):
    # print(tree._data)
    queue = []
    queue.append(tree)
    while True:
        if queue==[]:
            break
        print(queue[0]._data)
        first_tree = queue[0]
        if first_tree._left != None:
            queue.append(first_tree._left)
        if first_tree._right != None:
            queue.append(first_tree._right)
        queue.remove(first_tree)

if __name__ == '__main__':

    tree = Node('A',Node('B',Node('D'),Node('E')),Node('C',Node('F'),Node('G')))
    pro_order(tree)
    mid_order(tree)
    pos_order(tree)

4、递归算法

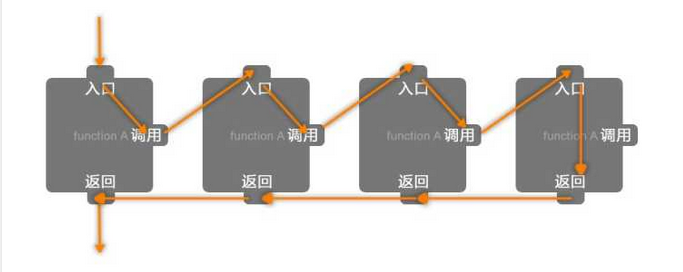
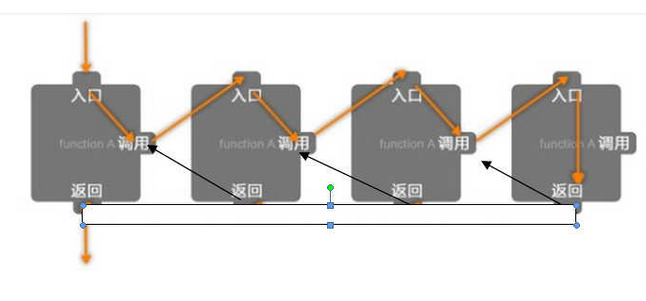
上面两张图片是从知乎贴过来的；图1中返回后会直接返回到上一级的返回，这种想法是不全面的，较合理的返回应该是如图2 在子函数返回时应返回到调用子函数的节点，这样在执行完剩余代码再返回到上一级

如果是按照图1返回的话二叉树的遍历就不能按照上例来实现。

#递归求N!
def recursive_mix(n):
    if n == 2:
        return 1
    return n*recursive_mix(n-1)

#十进制转二进制
def recursive_conversion(n):
    if n == 0:
        return

    recursive_conversion(int(n/2))
    print(n%2)
    # return n%2

#递归实现数字倒叙
def recursive_back(n):
    if n ==0:
        return
    print(n%10)
    recursive_back(int(n/10))

recursive_conversion(23)
recursive_mix(5)
recursive_back(1234)