[MCSM] Slice Sampler

1. 引言

之前介绍的MCMC算法都具有一般性和通用性（这里指Metropolis-Hasting 算法），但也存在一些特殊的依赖于仿真分布特征的MCMC方法。在介绍这一类算法（指Gibbs sampling）之前，本节将介绍一种特殊的MCMC算法。 我们重新考虑了仿真的理论基础，建立了Slice Sampler。

考虑到[MCSM]伪随机数和伪随机数生成器中提到的产生服从f(x)密度分布随机数等价于在子图f上产生均匀分布，即

类似笔记“[MCSM] Metropolis-Hastings 算法”（文章还没写好），考虑采用马尔可夫链的稳态分布来等价上的均匀分布，以此作为f分布的近似。很自然的想法是采用随机行走（random walk）。这样得到的稳态分布是在集合上的均匀分布。

2. 2D slice sample

有很多方法实现在集合上的"random walk"，最简单的就是一次改变一个方向上的取值，每个方向的改变交替进行，由此得到的算法是 2D slice sampler

---

在第t次迭代中，执行

1.

2. ， 其中

---

举例

其中，是归一化因子，代码如下，第一幅图是前10个点的变化轨迹，第二幅图表明初始点的选取影响不大

% p324
T = :;
T = T/;
% N(,)
y = exp(-(T+).^/);
plot(T,y);
hold on;
x = 0.25;
u = rand *(exp(-(x+).^/));
x_s = [x];
u_s = [u];
for k = :;
    limit = - + sqrt(-*log(u));
    limit = min([limit ]);
    x = rand * limit;
    x_s = [x_s x];
    u_s = [u_s u];
    u = rand *(exp(-(x+).^/));
    x_s = [x_s x];
    u_s = [u_s u];
end
plot(x_s,u_s,'-*');
hold off;

%%
x = 0.01;
u = 0.01;
x_s = [x];
u_s = [u];
for k = :;
    limit = - + sqrt(-*log(u));
    limit = min([limit ]);
    x = rand * limit;
    x_s = [x_s x];
    u_s = [u_s u];
    u = rand *(exp(-(x+).^/));
    x_s = [x_s x];
    u_s = [u_s u];
end
figure;
subplot(,,);
plot(x_s,u_s,'*');hold on;plot(T,y);
x = 0.99;
u = 0.0001;
x_s = [x];
u_s = [u];
for k = :;
    limit = - + sqrt(-*log(u));
    limit = min([limit ]);
    x = rand * limit;
    x_s = [x_s x];
    u_s = [u_s u];
    u = rand *(exp(-(x+).^/));
    x_s = [x_s x];
    u_s = [u_s u];
end
subplot(,,);
plot(x_s,u_s,'*');hold on;plot(T,y);
x = 0.25;
u = 0.0025;
x_s = [x];
u_s = [u];
for k = :;
    limit = - + sqrt(-*log(u));
    limit = min([limit ]);
    x = rand * limit;
    x_s = [x_s x];
    u_s = [u_s u];
    u = rand *(exp(-(x+).^/));
    x_s = [x_s x];
    u_s = [u_s u];
end
subplot(,,);
plot(x_s,u_s,'*');hold on;plot(T,y);

3. General Slice Sampler

有时候面临的概率密度函数不会那么简单，此时面临的困难主要在于无法在第二次更新的时候找到集合的范围。但有时我们可以将概率密度函数分解为多个较为简单的函数之积，即

---

    Slice Sampler

1.

2.  ，其中

---

看着挺高级好用的，实际上也只是能用的，一是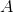本身就很难求，第二是即使求出来了，这个满足均匀分布的变量也很难得到，比如说书上的例子（Example 8.3）

很自然的分成了

但是集合完全没有办法用，求其中一个，然后拒绝不满足要求的看起来是可行的，但是效率实在是太低了（效率低实际上是我写错了，实际上还可以）

代码如下（代码是MATLAB的，画出来的图不好看，这个图是作者的R代码画出来的）

x = ;
u1 = rand*(+sin(*x)^);
u2 = rand*(+cos(*x)^);
u3 = rand*(exp(-x^/));
x_s = zeros(,);
for k = :
    limit = sqrt(-*log(u3));
    x = -limit + *limit*rand;
    while((sin(*x))^<u1- || (cos(*x))^<u2-)
        x = -limit + *limit*rand;
    end
    u1 = rand*(+sin(*x)^);
    u2 = rand*(+cos(*x)^);
    u3 = rand*(exp(-x^/));
    x_s(k) = x;
end
hist(x_s,);

4. 收敛性

不会