3.1、Factorization Machine模型

Factorization Machine模型

　　在Logistics Regression算法的模型中使用的是特征的线性组合，最终得到的分隔超平面属于线性模型，其只能处理线性可分的二分类问题，现实生活中的分类问题是多中多样的，存在大量的非线性可分的分类问题。

　　为了使得Logistics Regression算法能够处理更多的复杂问题，对Logistics Regression算法精心优化主要有两种，（1）对特征进行处理，如核函数的方法，将非线性可分问题转换为近似线性可分的问题（2）对Logistics Regression算法进行扩展，因子分解机（Factorization Machine，FM）是对基本Logistics Regression算法的扩展，是由Steffen Rendle提出的一种基于矩阵分解的机器学习算法。

1、Logistics Regression算法的不足:

　　由于Logistics Regression算法简单，易于实现的特点，在工业界中得到广泛的使用，但是基本的Logistics Regression算法只能处理线性可分的二分类问题，对于下图的非线性可分的二分类问题，基本的Logistics Regression算法却不能够很好的进行分类。

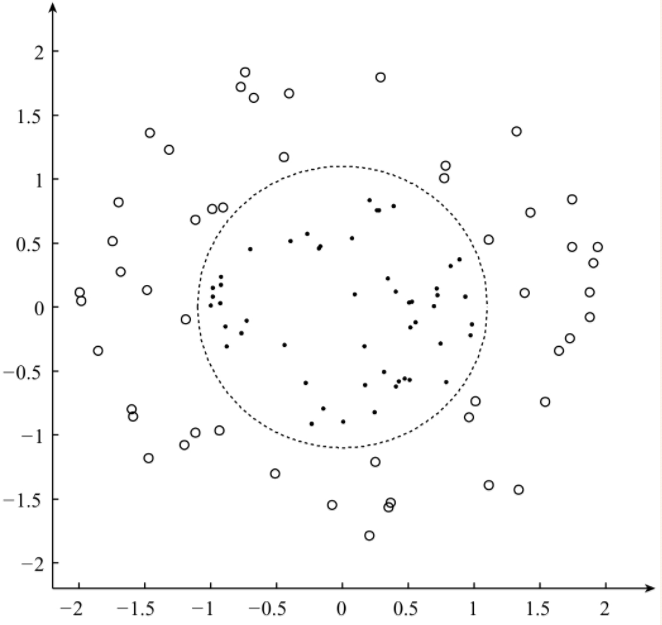
基本的Logistics Regression算法不能很好的将上述的数据分开，为了能够利用Logistics Regression算法处理非线性可分的数据，通常有两种方法，（1）利用人工对特征进行处理，使用核函数对特征进行处理，对于上图所示对的数据，利用函数f（x）=x²进行特征处理处理后的数据如下图，（2）对于基本的Logistic Regression算法进行扩展，以适应更难分类问题。

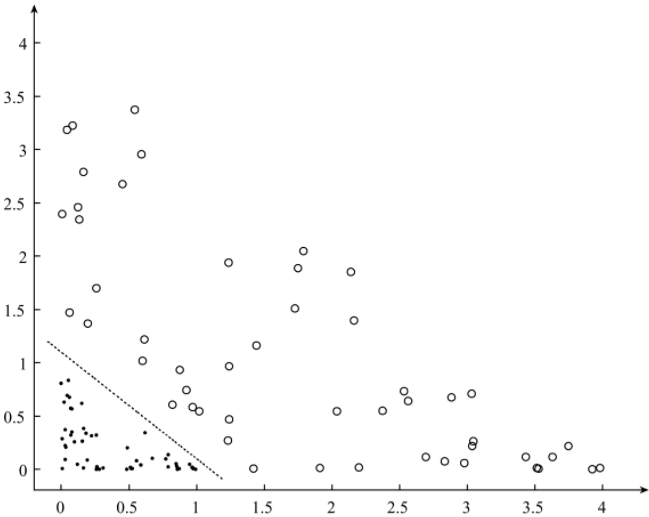
　　因子分解机（Factorization Machine，FM）算法是对Logistics Regression算法的扩展，在因子分解机FM模型中，不仅包含了Logistics Regression模型中的线性项，还包含了非线性的交叉项，利用矩阵分解的方法对，模型中的交叉项的系数学习，得到每一项的系数，而无需人工参与。

理解：在线性模型中，我们假设的是所有的特征之间是没有相互影响的。所有我们可以用线性模型f(x)=x*w+b但是在实际问题中，可能会出现两个特征或者多个特征的相互影响，所以这里就引入因子分解机模型，这里有一个度的问题，这里的度就是指有多少个特征之间影响，如果是两个特征之间相互影响这里的度就是2，如果是三次特征之间相互影响，这里的度就是3.但是我们一般处理的都是度为2 的问题。

 1、因子分解模型

　　FM是一般线性模型的推广，一般的线性模型可以表示为(式0)：

　　                               

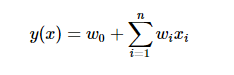
但是上述模型没有考虑特征间的关联，为表示关联特征对y的影响，引入多项式模型，以xiyi表示两特征的组合，有如下二阶多项式模型(式1)：

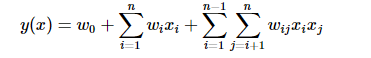
　　　对于因子分解机模型FM模型，引入度的概念。对于度为2的因子分解机FM的模型为：

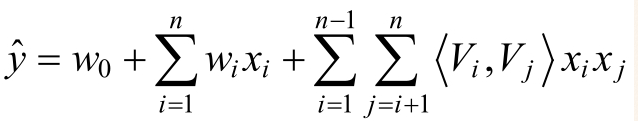
　　其中，参数w0∈R，W∈Rⁿ，V∈R^n×k。<Vi,Vj>表示的是两个大小为k的向量Vi和Vj的点积。

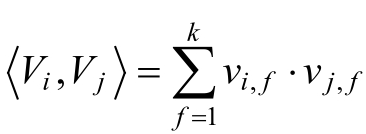
　　其中，V_i表示的是系数矩阵V的第i维为向量，且V_i = （vi，₁，v_i，2，.......v_i，k），K∈N⁺称为超参数，且k的大小称为因子分解机FM算法的度。在因子分解机机FM模型中，前面两部分是传统的线性模型，最后一部分将两个互异特征分量之间的相互关系考虑进来。

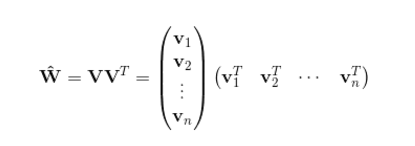
2、因子分解机可以处理的问题

• 回归问题
• 二分类问题
• 排序问题

　　对于处理回归问题，其最终的形式为：

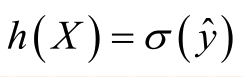
　　其中，∂阀值函数，通常取为Sigmoid函数：

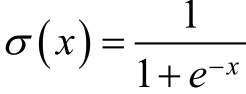
3、二分类因子分解机FM算法的损失函数：

　　使用logit loss作为优化标准，即：

      

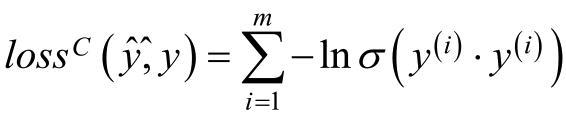
　　FM算法中交叉项的处理

1.交叉项系数：

　　　　　　在基本线性回归模型的基础上引入交叉项，如下：

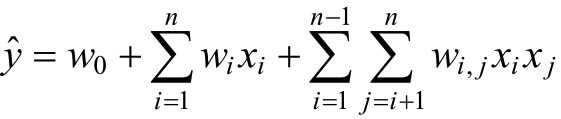
　　　　　　这种直接在交叉项x_ix_j的前面加上交叉项系数w_i，j的方式，在稀疏数据的情况下存在一个很大的缺陷，即在对于观察样本中为未出现交互特征分量时，不能对相应的参数进行估计。对每一个特征分量x_i引入辅助向量V_i = （vi，1，vi，2，.......vi，k），利用ViVj^T对交叉项的系数w_i，j进行估计即：

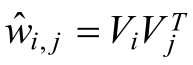
令：

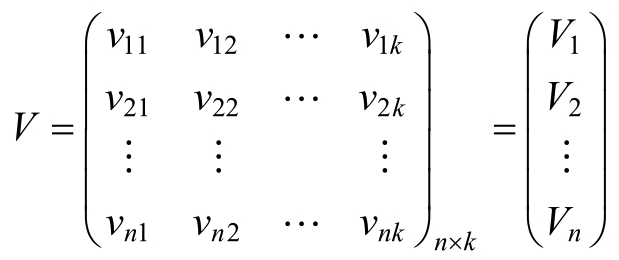
则：

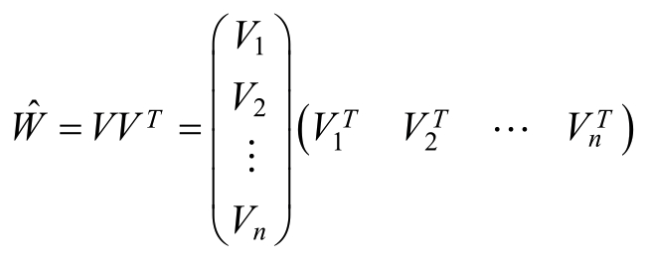
　　这就对应于了一种矩阵的分解，对k值得限定、FM的表达能力均有一定的影响。

 模型的求解：

　　　　对于交叉项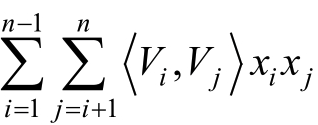的求解，可以采用公式：

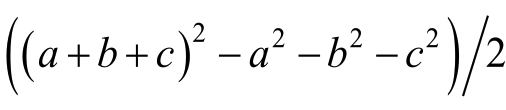
其具体过程如下：

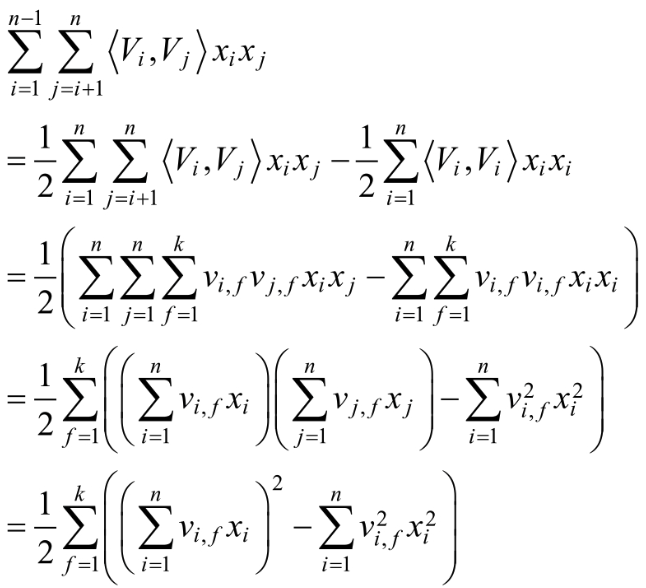
3、FM算法求解：

　　对于FM算法的求解，主要利用了梯度下降法。

　　3.1、随机梯度下降（SGD）

　　　　随机梯度下降在每次迭代的过程中，仅根据一个样本对模型中的参数进行调整。

　　随机梯度下降法的优化过程为：

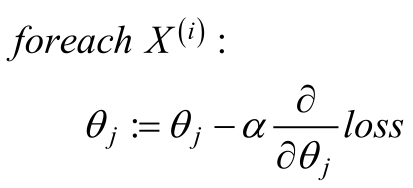
　　　　假设数据集中有m个训练样本，即{X（1）,X（2）,........X（i）}，每个样本X（i）有n个特征即

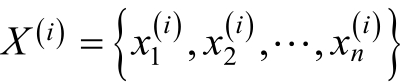
对于度为2 的因子分解机FM模型，其主要的参数有一次项和常数项的参数w_0，w_1，....w_n以及交叉项的系数矩阵V。在利随机梯度对模型的参数进行学习的过程中，主要是对损失函数求导，即：

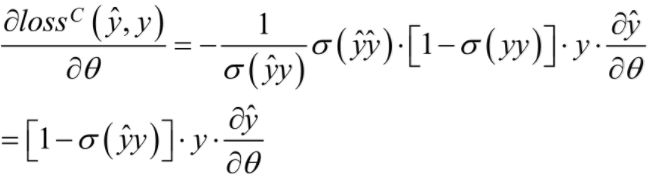
而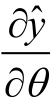：为：

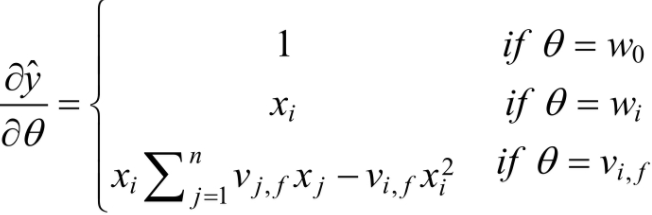
　　3.2、FM算法流程：

　　利用随机梯度下降算法对因子分解机FM模型中的参数进行学习的基本步骤如下：

　　1.初始化权重w_0，w_1，....w_n和V

　　2.对每一个样本：

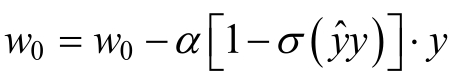
　　对特征i∈{1，.....n}：

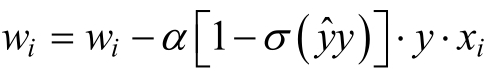
　　3.重复步骤2，直到满足终止条件

4、用Python实现

　　利用随机梯度下降训练FM模型

 def stocGradAscent(dataMatrix, classLabels, k, max_iter, alpha):
     '''利用随机梯度下降法训练FM模型
     input:  dataMatrix(mat)特征
             classLabels(mat)标签
             k(int)v的维数
             max_iter(int)最大迭代次数
             alpha(float)学习率
     output: w0(float),w(mat),v(mat):权重
     '''
     m, n = np.shape(dataMatrix)
     # 1、初始化参数
     w = np.zeros((n, 1))  # 其中n是特征的个数
     w0 = 0  # 偏置项
     v = initialize_v(n, k)  # 初始化V

     # 2、训练
     for it in range(max_iter):
         for x in range(m):  # 随机优化，对每一个样本而言的
             inter_1 = dataMatrix[x] * v
             inter_2 = np.multiply(dataMatrix[x], dataMatrix[x]) * \
              np.multiply(v, v)  # multiply对应元素相乘
             # 完成交叉项
             interaction = np.sum(np.multiply(inter_1, inter_1) - inter_2) / 2.
             p = w0 + dataMatrix[x] * w + interaction  # 计算预测的输出
             loss = sigmoid(classLabels[x] * p[0, 0]) - 1

             w0 = w0 - alpha * loss * classLabels[x]
             for i in range(n):
                 if dataMatrix[x, i] != 0:
                     w[i, 0] = w[i, 0] - alpha * loss * classLabels[x] * dataMatrix[x, i]

                     for j in range(k):
                         v[i, j] = v[i, j] - alpha * loss * classLabels[x] * \
                         (dataMatrix[x, i] * inter_1[0, j] -\
                           v[i, j] * dataMatrix[x, i] * dataMatrix[x, i])

         # 计算损失函数的值
         if it % 1000 == 0:
             print ("\t------- iter: ", it, " , cost: ", \
             getCost(getPrediction(np.mat(dataMatrix), w0, w, v), classLabels))

     # 3、返回最终的FM模型的参数
     return w0, w, v

初始化交叉的权重：

 def initialize_v(n, k):
     '''初始化交叉项
     input:  n(int)特征的个数
             k(int)FM模型的超参数
     output: v(mat):交叉项的系数权重
     '''
     v = np.mat(np.zeros((n, k)))

     for i in range(n):
         for j in range(k):
             # 利用正态分布生成每一个权重
             v[i, j] = normalvariate(0, 0.2)
     return v

为了能够使用正态分布对权重进行初始化，我们需要导入normalvariate函数

from random import normalvariate

　Sigmoid函数

def sigmoid(inx):
    return 1.0/(1+np.exp(-inx))

　　计算当前的损失函数的值：

 def getCost(predict, classLabels):
     '''计算预测准确性
     input:  predict(list)预测值
             classLabels(list)标签
     output: error(float)计算损失函数的值
     '''
     m = len(predict)
     error = 0.0
     for i in range(m):
         error -=  np.log(sigmoid(predict[i] * classLabels[i] ))
     return error