Fast Matrix Operations UVA - 11992 线段树

题意翻译

有一个r行c列的全0矩阵，有以下三种操作。

• 1 X1 Y1 X2 Y2 v 子矩阵（X1,Y1,X2,Y2）的元素加v

• 2 X1 Y1 X2 Y2 v 子矩阵（X1,Y1,X2,Y2）的元素变为v

• 3 X1 Y1 X2 Y2 查询子矩阵（X1,Y1,X2,Y2）的和，最大值，最小值

子矩阵（X1,Y1,X2,Y2）满足X1<=X<=X2 Y1<=Y<=Y2的所有元素（X1,Y2）。

输入保证和不超过10^9

感谢@Himself65 提供的翻译

题目描述

PDF

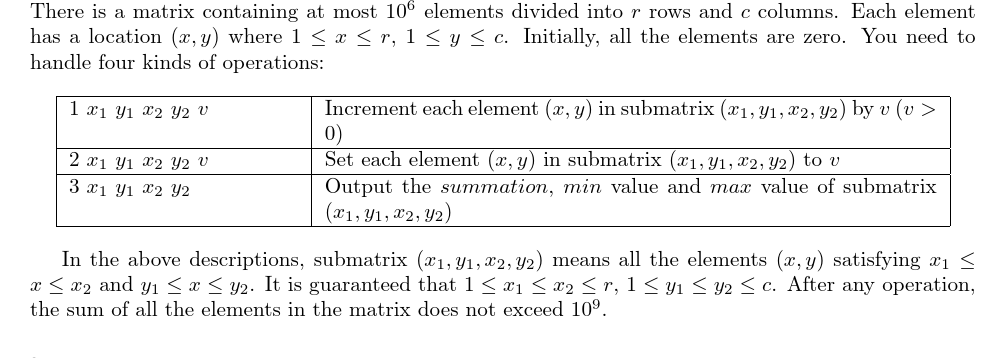
输入输出格式

输入格式：

输出格式：

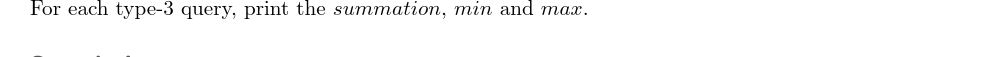
输入输出样例

输入样例#1：
复制

4 4 8
1 1 2 4 4 5
3 2 1 4 4
1 1 1 3 4 2
3 1 2 4 4
3 1 1 3 4
2 2 1 4 4 2
3 1 2 4 4
1 1 1 4 3 3

输出样例#1： 复制

45 0 5
78 5 7
69 2 7
39 2 7
注意setv和addv的优先级，当有setv时，addv就不应该再有影响；

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstdlib>
#include<cstring>
#include<string>
#include<cmath>
#include<map>
#include<set>
#include<vector>
#include<queue>
#include<bitset>
#include<ctime>
#include<time.h>
#include<deque>
#include<stack>
#include<functional>
#include<sstream>
//#include<cctype>
//#pragma GCC optimize(2)
using namespace std;
#define maxn 2000005
#define inf 0x7fffffff
//#define INF 1e18
#define rdint(x) scanf("%d",&x)
#define rdllt(x) scanf("%lld",&x)
#define rdult(x) scanf("%lu",&x)
#define rdlf(x) scanf("%lf",&x)
#define rdstr(x) scanf("%s",x)
#define mclr(x,a) memset((x),a,sizeof(x))
typedef long long  ll;
typedef unsigned long long ull;
typedef unsigned int U;
#define ms(x) memset((x),0,sizeof(x))
const long long int mod = 1e9 + 7;
#define Mod 1000000000
#define sq(x) (x)*(x)
#define eps 1e-5
typedef pair<int, int> pii;
#define pi acos(-1.0)
//const int N = 1005;
#define REP(i,n) for(int i=0;i<(n);i++)
typedef pair<int, int> pii;

inline int rd() {
	int x = 0;
	char c = getchar();
	bool f = false;
	while (!isdigit(c)) {
		if (c == '-') f = true;
		c = getchar();
	}
	while (isdigit(c)) {
		x = (x << 1) + (x << 3) + (c ^ 48);
		c = getchar();
	}
	return f ? -x : x;
}

ll gcd(ll a, ll b) {
	return b == 0 ? a : gcd(b, a%b);
}
int sqr(int x) { return x * x; }

/*ll ans;
ll exgcd(ll a, ll b, ll &x, ll &y) {
	if (!b) {
		x = 1; y = 0; return a;
	}
	ans = exgcd(b, a%b, x, y);
	ll t = x; x = y; y = t - a / b * y;
	return ans;
}
*/

struct node {
	int sum[maxn], minn[maxn], maxx[maxn], ls[maxn], rs[maxn], setv[maxn], addv[maxn];
	int tt, rt;
	void init() {
		tt = rt = 1; mclr(setv, -1); ms(addv);
		ms(sum); ms(minn); ms(maxx); ms(ls); ms(rs);
	}
	void pushup(int o) {
		sum[o] = sum[ls[o]] + sum[rs[o]];
		minn[o] = min(minn[ls[o]], minn[rs[o]]);
		maxx[o] = max(maxx[ls[o]], maxx[rs[o]]);
	}
	void pushdown(int o,int l,int r) {
		if (setv[o]!=-1) {
			int mid = (l + r) >> 1;
			if (!ls[o])ls[o] = ++tt; if (!rs[o])rs[o] = ++tt;
			sum[ls[o]] = setv[o] * (mid - l + 1);
			sum[rs[o]] = setv[o] * (r - mid);
			minn[ls[o]] = minn[rs[o]] = maxx[ls[o]] = maxx[rs[o]] = setv[o];
			setv[ls[o]] = setv[o]; setv[rs[o]] = setv[o]; setv[o] = -1; addv[ls[o]] = addv[rs[o]] = 0;
		}
		if (addv[o]) {
			int mid = (l + r) >> 1;
			if (!ls[o])ls[o] = ++tt; if (!rs[o])rs[o] = ++tt;
			sum[ls[o]] += addv[o] * (mid - l + 1); sum[rs[o]] += addv[o] * (r - mid);
			maxx[ls[o]] += addv[o]; maxx[rs[o]] += addv[o];
			minn[ls[o]] += addv[o]; minn[rs[o]] += addv[o];
			addv[ls[o]] += addv[o]; addv[rs[o]] += addv[o];
			addv[o] = 0;
		}
	}
	void upd(int &o, int L, int R, int l, int r, int opt,int val) {
		if (!o) {
			o = ++tt;
		}
		if (L <= l && r <= R) {
			if (opt == 1) {
				sum[o] += (r - l + 1)*val;
				maxx[o] += val; minn[o] += val;
				addv[o] += val;
			}
			else {
				sum[o] = (r - l + 1)*val;
				maxx[o] = val; minn[o] = val;
				setv[o] = val; addv[o] = 0;
			}
			return;
		}
		pushdown(o, l, r);
		int mid = (l + r) >> 1;
		if (L <= mid)upd(ls[o], L, R, l, mid, opt, val);
		if (mid < R)upd(rs[o], L, R, mid + 1, r, opt, val);
		pushup(o);
	}
	int Sum(int L, int R, int l, int r, int o) {
		if (L <= l && r <= R) {
			return sum[o];
		}
		pushdown(o, l, r);
		int mid = (l + r) >> 1;
		int ans = 0;
		if (L <= mid)ans += Sum(L, R, l, mid, ls[o]);
		if (mid < R)ans += Sum(L, R, mid + 1, r, rs[o]);
		return ans;
	}
	int Max(int L, int R, int l, int r, int o) {
		if (L <= l && r <= R)return maxx[o];
		pushdown(o, l, r);
		int mid = (l + r) >> 1;
		int MAX = -inf;
		if (L <= mid)MAX = max(MAX, Max(L, R, l, mid, ls[o]));
		if (mid < R)MAX = max(MAX, Max(L, R, mid + 1, r, rs[o]));
		return MAX;
	}
	int Min(int L, int R, int l, int r, int o) {
		if (L <= l && r <= R)return minn[o];
		pushdown(o, l, r);
		int mid = (l + r) >> 1;
		int MIN = inf;
		if (L <= mid)MIN = min(MIN, Min(L, R, l, mid, ls[o]));
		if (mid < R)MIN = min(MIN, Min(L, R, mid + 1, r, rs[o]));
		return MIN;
	}
}t[22];

int main()
{
	//	ios::sync_with_stdio(0);
	int r, c, m;
	while (cin >> r >> c >> m) {
		for (int i = 1; i <= r; i++)t[i].init();
		while (m--) {
			int opt = rd();
			if (opt == 1) {
				int X1 = rd(), Y1 = rd(), X2 = rd(), Y2 = rd(), v = rd();
				for (int i = X1; i <= X2; i++)t[i].upd(t[i].rt, Y1, Y2, 1, c, 1, v);
			}
			else if (opt == 2) {
				int X1 = rd(), Y1 = rd(), X2 = rd(), Y2 = rd(), v = rd();
				for (int i = X1; i <= X2; i++)t[i].upd(t[i].rt, Y1, Y2, 1, c, 2, v);
			}
			else {
				int ans = 0, ans1 = inf, ans2 = -inf;
				int X1 = rd(), Y1 = rd(), X2 = rd(), Y2 = rd();
				for (int i = X1; i <= X2; i++) {
					ans += t[i].Sum(Y1, Y2, 1, c, t[i].rt);
					ans1 = min(ans1, t[i].Min(Y1, Y2, 1, c, t[i].rt));
					ans2 = max(ans2, t[i].Max(Y1, Y2, 1, c, t[i].rt));
				}
				printf("%d %d %d\n", ans, ans1, ans2);
			}
		}
	}
	return 0;
}