时间序列算法理论及python实现（2-python实现）

如果你在寻找时间序列是什么？如何实现时间序列？那么请看这篇博客，将以通俗易懂的语言，全面的阐述时间序列及其python实现。

时间序列算法理论详见我的另一篇博客：时间序列算法理论及python实现 - 知-青 - 博客园

5 Python实现ARIMA模型

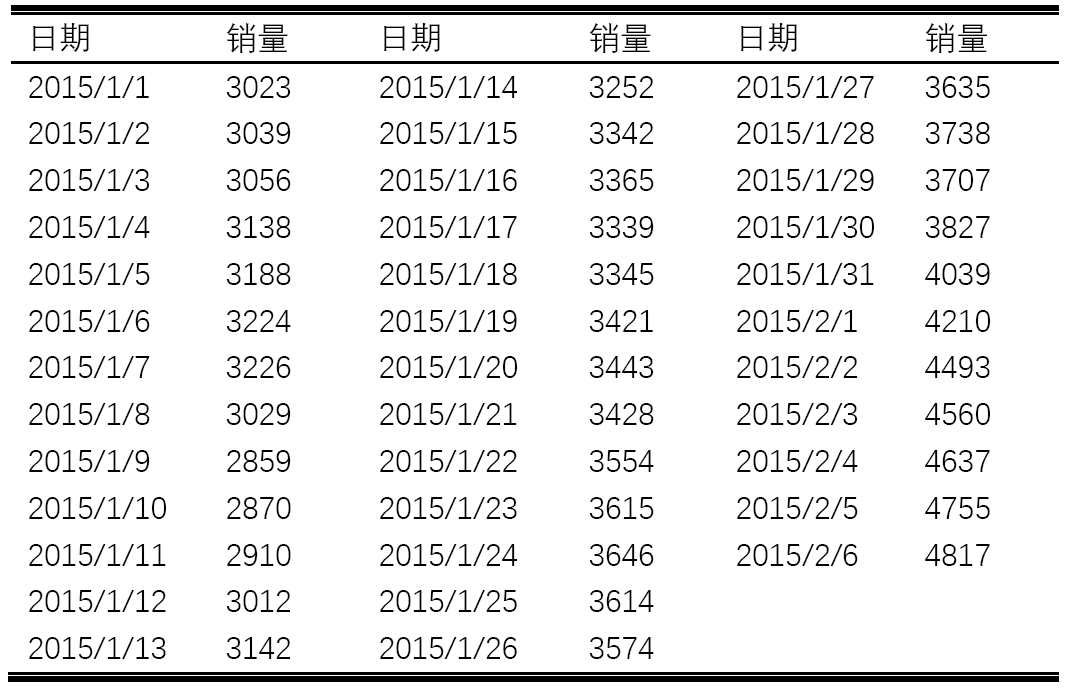
下面应用以上理论知识，对表6中2015/1/1~2015/2/6某餐厅的销售数据进行建模。

就餐饮企业而言，经常会碰到如下问题。

由于餐饮行业是胜场和销售同时进行的，因此销售预测对于餐饮企业十分必要。如何基于菜品历史销售数据，做好餐销售预测，以便减少菜品脱销现象和避免因备料不足而造成的生产延误，从而减少菜品生产等待时间，提供给客户更优质的服务，同事可以减少安全库存量，做到生产准时制，降低物流成本

餐饮销售预测可以看作是基于时间序列的短期数据预测，预测对象为具体菜品销售量

表6 原序列数据

5.1 环境配置

 import pandas as pd
 import matplotlib.pyplot as plt
 from matplotlib.pylab import style
 from statsmodels.tsa.stattools import adfuller as ADF
 from statsmodels.stats.diagnostic import acorr_ljungbox  # 白噪声检验
 from statsmodels.tsa.arima_model import ARIMA
 import statsmodels.tsa.api as smt
 import seaborn as sns
 style.use('ggplot')
 plt.rcParams['font.sans-serif'] = ['SimHei']  # 用来正常显示中文标签
 plt.rcParams['axes.unicode_minus'] = False  # 用来正常显示负号

要安装的环境有点小多，需要提前安装好。

5.2 导入数据

 # 参数初始化
 discfile = './data/arima_data.xls'
 forecastnum = 5

 # 读取数据，指定日期列为指标，Pandas自动将“日期”列识别为Datetime格式
 data = pd.read_excel(discfile, index_col=u'日期')

代码和数据将会公布在Github，请到文末链接。

5.3 检验序列的平稳性

 # 时序图
 import matplotlib.pyplot as plt
 plt.rcParams['font.sans-serif'] = ['SimHei']  # 用来正常显示中文标签
 plt.rcParams['axes.unicode_minus'] = False  # 用来正常显示负号
 data.plot()
 plt.show()

 # 自相关图
 from statsmodels.graphics.tsaplots import plot_acf
 plot_acf(data).show()

 # 平稳性检测
 from statsmodels.tsa.stattools import adfuller as ADF
 print(u'原始序列的ADF检验结果为：', ADF(data[u'销量']))
 # 返回值依次为adf、pvalue、usedlag、nobs、critical values、icbest、regresults、resstore

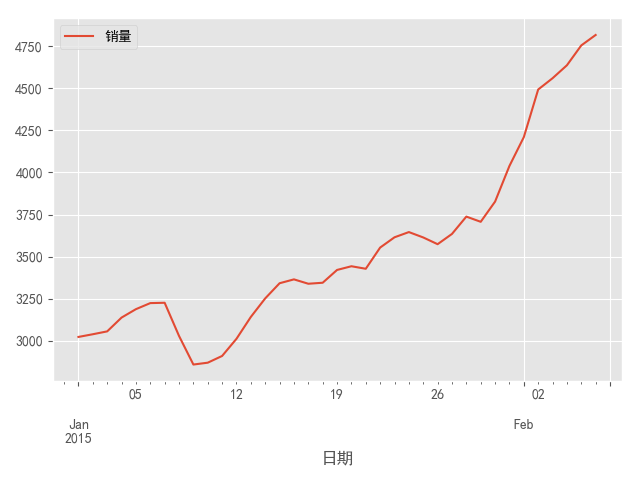
图3 原始序列的时序图

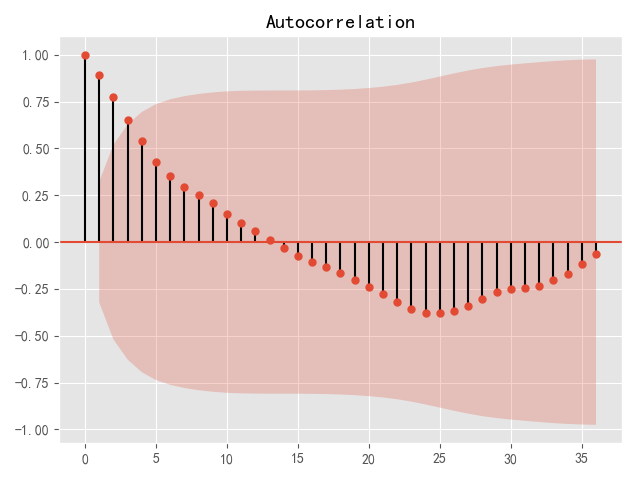
图4 原始序列的自相关图

原始时间序列的单位根检验

表7 原始序列的单位根检验

图3时序图显示该序列具有明显的单调递增趋势，可以判断为是非平稳序列；图4的自相关图显示自相关系数长期大于零，说明序列间具有很强的长期相关性；表7单位根检验统计量对应的P值显著大于0.05，最终将该序列判断为非平稳序列（非平稳序列一定不是白噪声序列）。

5.4 对原始序列进行一阶差分，并进行平稳性和白噪声检验

5.4.1 对一阶差分后的序列再次做平稳性判断

 # 差分后的结果
 D_data = data.diff().dropna()
 D_data.columns = [u'销量差分']
 D_data.plot()  # 时序图
 plt.show()
 plot_acf(D_data).show()  # 自相关图
 from statsmodels.graphics.tsaplots import plot_pacf
 plot_pacf(D_data).show()  # 偏自相关图
 print(u'差分序列的ADF检验结果为：', ADF(D_data[u'销量差分']))  # 平稳性检测

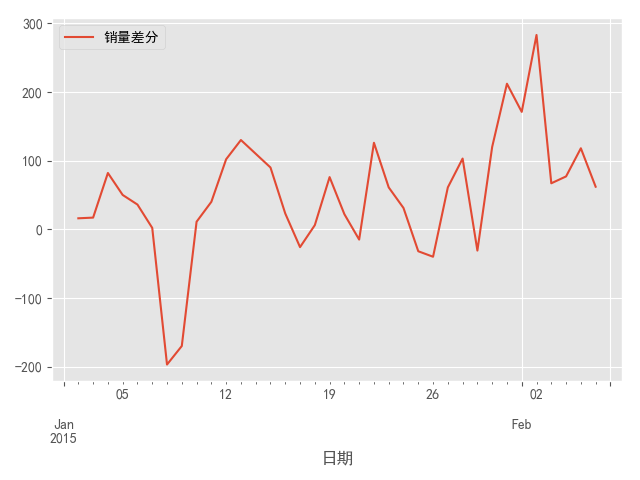
图5 一阶差分之后序列的时序图

图6 一阶差分之后序列的自相关图

一阶差分之后序列的单位根检验

表8 一阶差分之后序列的单位根检验

结果显示，一阶差分之后的序列的时序图在均值附近比较平稳的波动、自相关图有很强的短期相关性、单位根检验P值小于0.05，所以一阶差分之后的序列是平稳序列。

5.4.2 对一阶差分后的序列做白噪声检验（结果见表5-28）

from statsmodels.stats.diagnostic import acorr_ljungbox
print(u'差分序列的白噪声检验结果为：', acorr_ljungbox(D_data, lags=1))  # 返回统计量和p值

表9 一阶差分后的序列的白噪声检验

输出的P值远远小于0.05，所以一阶差分之后的序列是平稳非白噪声序列。

5.5 对一阶差分之后的平稳非白噪声序列拟合ARMA模型

下面进行模型定阶，模型定阶就是确定p和q。

5.5.1 人为识别实现模型定阶

一阶差分后自相关图（见图6）显示出1阶截尾，偏自相关图显示出拖尾性，所以可以考虑用MA(1)模型拟合1阶差分后的序列，即对原始序列建立ARIMA(0,1,1)模型。

图7 一阶差分后序列的偏自相关图

5.5.2 相对最优模型识别

计算ARMA(p,q)。当p和q均小于等于3的所有组合的BIC信息量，取其中BIC信息量达到最小的模型阶数。

 from statsmodels.tsa.arima_model import ARIMA

 data[u'销量'] = data[u'销量'].astype(float)
 # 定阶
 pmax = int(len(D_data) / 10)  # 一般阶数不超过length/10
 qmax = int(len(D_data) / 10)  # 一般阶数不超过length/10
 bic_matrix = []  # bic矩阵
 for p in range(pmax + 1):
     tmp = []
     for q in range(qmax + 1):
         try:  # 存在部分报错，所以用try来跳过报错。
             tmp.append(ARIMA(data, (p, 1, q)).fit().bic)
         except:
             tmp.append(None)
     bic_matrix.append(tmp)

 bic_matrix = pd.DataFrame(bic_matrix)  # 从中可以找出最小值

 p, q = bic_matrix.stack().idxmin()  # 先用stack展平，然后用idxmin找出最小值位置。
 print(u'BIC最小的p值和q值为：%s、%s' % (p, q))

计算完成BIC矩阵如下（绘制程序在主程序，以上程序仅仅只有计算）

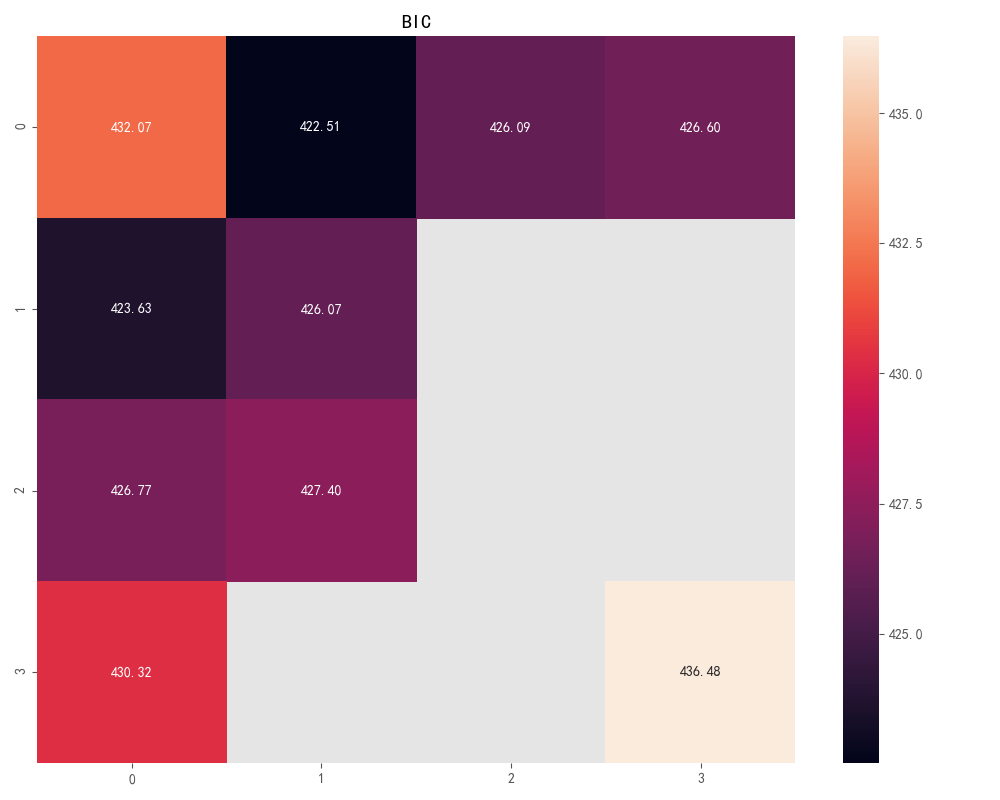
图8 矩阵热度图

P值为0、q值为1时最小BIC值为：430.1374。p、q定阶完成！

5.6 模型检验

用AR(1)模型拟合一阶差分后的序列，即对原始序列建立ARIMA(0,1,1)模型。虽然两种方法建立的模型是一样，但模型是非唯一的，可以检验ARIMA(1,1,0)和ARIMA(1,1,1)，这两个模型也能通过检验。

下面对一阶差分后的序列拟合AR(1)模型进行分析。

（1）模型检验。残差为白噪声序列，p值为：0.627016

（2）参数检验和参数估计见表10。

表10 模型参数

5.7 模型预测

 model = ARIMA(data, (p, 1, q)).fit()  # 建立ARIMA(0, 1, 1)模型
 model.summary2()  # 给出一份模型报告
 model.forecast(5)  # 作为期5天的预测，返回预测结果、标准误差、置信区间。

应用ARIMA(0,1,1)对表11中的2015/1/1~2015/2/6某餐厅的销售数据做为期5天的预测，结果如下。

表11 预测结果

需要说明的是，利用模型向前预测的时期越长，预测误差将会越大，这是时间预测的典型特点。

6 文献

王黎明，王连等. 应用时间序列分析

张良均，王路，谭立云，苏剑林. Python数据分析与挖掘实战

python时间序列分析 - 大熊猫淘沙 - 博客园

机器学习_时间序列预测分析算法 | FEI's Blog

ARIMA模型的拖尾截尾问题 - CSDN博客

时间序列初级理论篇 - CSDN博客

大数据时间序列分析、建模与预测系列 第一部分: 数据准备

Complete guide to create a Time Series Forecast (with Codes in Python)

时间序列预测如何变成有监督学习问题？ - 云+社区 - 腾讯云

时间序列 - 用户指南| 阿里云

7 附录：程序及数据

说明：为了方便调用，我把所有程序都封装成函数，调用极其方便只用改动很小的参数。

 # -*- coding:utf-8 -*-
 # @Time    : 2018/7/11 15:18
 # @Author  : yuanjing liu
 # @Email   : lauyuanjing@163.com
 # @File    : ts_arima.py
 # @Software: PyCharm
 # arima时序模型

 import pandas as pd
 import matplotlib.pyplot as plt
 from matplotlib.pylab import style
 from statsmodels.tsa.stattools import adfuller as ADF
 from statsmodels.stats.diagnostic import acorr_ljungbox  # 白噪声检验
 from statsmodels.tsa.arima_model import ARIMA
 import statsmodels.tsa.api as smt
 import seaborn as sns
 style.use('ggplot')
 plt.rcParams['font.sans-serif'] = ['SimHei']  # 用来正常显示中文标签
 plt.rcParams['axes.unicode_minus'] = False  # 用来正常显示负号

 # 对原始数据进行ACF、PACF检验
 def tsplot(y, lags=None, title='', figsize=(14, 8)):
     fig = plt.figure(figsize=figsize)
     layout = (2, 2)
     ts_ax = plt.subplot2grid(layout, (0, 0))
     hist_ax = plt.subplot2grid(layout, (0, 1))
     acf_ax = plt.subplot2grid(layout, (1, 0))
     pacf_ax = plt.subplot2grid(layout, (1, 1))

     y.plot(ax=ts_ax)
     ts_ax.set_title(title)
     y.plot(ax=hist_ax, kind='hist', bins=25)
     hist_ax.set_title('Histogram')
     smt.graphics.plot_acf(y, lags=lags, ax=acf_ax)
     smt.graphics.plot_pacf(y, lags=lags, ax=pacf_ax)
     [ax.set_xlim(0) for ax in [acf_ax, pacf_ax]]
     sns.despine()
     fig.tight_layout()
     plt.show()
     return ts_ax, acf_ax, pacf_ax

 # 平稳性检测(P值大于0.05，则存在单位根，是不平稳时间序列）
 # adf_jy返回值依次为adf、pvalue、usedlag、nobs、critical values、icbest、regresults、resstore
 def steady(sdata):
     adf_jy = ADF(sdata)  # data[u'销量']
     adf_p_value = adf_jy[1]
     return adf_jy, adf_p_value

 # 白噪声检验
 def w_noise(wdata):
     w_noise = acorr_ljungbox(wdata, lags=1)  # 返回统计量和p值
     w_p_value = float(w_noise[1])
     return w_noise, w_p_value

 # 差分后的结果（如果不平稳）
 def ts_diff(ddata):
     D_data = ddata.diff().dropna()  # dropna是缺失值处理
     D_data.columns = [u'1阶差分']
     return D_data

 def ts_arima(tsdata, forenum=5):
     tsdata = tsdata.astype(float)
     # 定阶
     D_data = ts_diff(tsdata)
     pmax = int(len(D_data) / 10)  # 一般阶数不超过length/10
     qmax = int(len(D_data) / 10)  # 一般阶数不超过length/10
     bic_matrix = []  # bic矩阵
     for p in range(pmax + 1):
         tmp = []
         for q in range(qmax + 1):
             try:  # 存在部分报错，所以用try来跳过报错。
                 tmp.append(ARIMA(tsdata, (p, 1, q)).fit().bic)
             except:
                 tmp.append(None)
         bic_matrix.append(tmp)

     bic_matrix = pd.DataFrame(bic_matrix)  # 从中可以找出最小值

     # 可视化BIC矩阵
     fig, ax = plt.subplots(figsize=(10, 8))
     ax = sns.heatmap(bic_matrix,
                      mask=bic_matrix.isnull(),
                      ax=ax,
                      annot=True,
                      fmt='.2f',
                      )
     ax.set_title('BIC')
     plt.show()

     p, q = bic_matrix.stack().idxmin()  # 先用stack展平，然后用idxmin找出最小值位置。
     # print(u'BIC最小的p值和q值为：%s、%s' % (p, q))

     model = ARIMA(tsdata, (p, 1, q)).fit()  # 建立ARIMA(0, 1, 1)模型
     summary = model.summary2()  # 给出一份模型报告
     forecast = model.forecast(forenum)  # 作为期forenum天的预测，返回预测结果、标准误差、置信区间。
     return bic_matrix, p, q, model, summary, forecast

 # 测试
 # 读取数据
 discfile = '../data/arima_data.xls'
 forecastnum = 5
 data = pd.read_excel(discfile, index_col=u'日期')
 ddata = data[u'销量']
 # 检验
 ts_ap = tsplot(ddata, title='A Given Training Series', lags=20)  # ACF 和 PACF 检验
 s_total, s_p = steady(ddata)  # 平稳性检验
 w_total, w_p = w_noise(ddata)
 # 差分
 dif_data = ts_diff(ddata)
 # arima模型
 bic_matrix1, p1, q1, model1, summary, forecast = ts_arima(ddata)

ts_arima_main

---

转载说明

1、本人博客纯属技术积累和分享，欢迎大家评论和交流以求共同进步。

2、在无明确说明下，博客可以转载以供个人学习和交流，但是要附上出处。

3、如果原创博客使用涉及商业/公司行为请邮件(1547364995@qq.com)告知，一般情况均会及时回复同意。

4、如果个人博客中涉及他人文章我会尽力注明出处，但受限于能力并不能保证所有引用之处均能够注明出处，如有冒犯，请您及时邮件告知以便修改，并于此提前向您道歉。

5、转载过程中如有涉及他人作品请您与作者联系。

6、所有文章（不限于原创）仅为个人见解，个人只能尽量保证正确，如有错误您需要自负责任，并请您留下评论提出错误之处以便及时更正，惠泽他人，谢谢