方格取数（dp）

方格取数

时间限制: 1 Sec  内存限制: 128 MB
提交: 9  解决: 4
[提交][状态][讨论版][命题人:quanxing]

题目描述

设有N×N的方格图，我们在其中的某些方格中填入正整数，而其它的方格中则放入数字0。如下图所示：

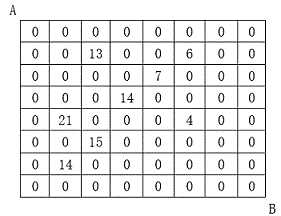
某人从图中的左上角A出发，可以向下行走，也可以向右行走，直到到达右下角的B点。在走过的路上，他可以取走方格中的数（取走后的方格中将变为数字0）。

此人从A点到B点共走了两次，试找出两条这样的路径，使得取得的数字和为最大。

输入

第一行为一个整数N（N≤10），表示N×N的方格图。

接下来的每行有三个整数，第一个为行号数，第二个为列号数，第三个为在该行、该列上所放的数。一行“0 0 0”表示结束。

输出

第一个整数，表示两条路径上取得的最大的和。

 

样例输入

8
2 3 13
2 6 6
3 5 7
4 4 14
5 2 21
5 6 4
6 3 15
7 2 14
0 0 0

样例输出

67

提示

 

来源

动态规划经典题

#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <algorithm>
#include <vector>
#include <queue>
#include<deque>
#define inf 0x3f3f3f3f
using namespace std;
int a[][];
int b[][];
int dp[][];
int main()
{
    int n;
    cin>>n;
    int i,j;
    memset(a,,sizeof(a));
     memset(dp,,sizeof(dp));
     int x,y,z;
    while(cin>>x>>y>>z)
    {
        if(x==&&y==&&z==) break;
        a[x][y]=z;
    }
    dp[][]=a[][];
    for( i=;i<=n;i++)
    {
        dp[][i]=dp[][i-]+a[][i];
        dp[i][]=dp[i-][]+a[i][];
    }
    for(i=;i<=n;i++)
    {
        for(j=;j<=n;j++)
        {
            dp[i][j]=a[i][j]+max(dp[i][j-],dp[i-][j]);
        }
    }
    int s=dp[n][n];
    i=n;j=n;
    b[i][j]=;
    for(int i=;i<=n;i++)
    {
        for(int j=;j<=n;j++)
            b[i][j]=a[i][j];
    }
    while(i!=||j!=)//回退看看是怎么退过来的
    {
        if(j>=&&dp[i][j]==a[i][j]+dp[i][j-])
        {
            b[i][j-]=;//要用一个新的数组，否则会影响，跳不出循环
            j--;
        }
        else if(i>=&&dp[i][j]==a[i][j]+dp[i-][j])
        {
            b[i-][j]=;
            i--;
        }
    }

    //for(int i=1;i<=n;i++)
    //{
    //    for(int j=1;j<=n;j++)
    //        cout<<a[i][j];
    //    cout<<endl;
    //}
 //  cout<<s<<endl;

    memset(dp,,sizeof(dp));
    dp[][]=b[][];
    for(i=;i<=n;i++)
    {
        dp[][i]=dp[][i-]+b[][i];
        dp[i][]=dp[i-][]+b[i][];
    }
    for(i=;i<=n;i++)
    {
        for(j=;j<=n;j++)
        {
            dp[i][j]=b[i][j]+max(dp[i][j-],dp[i-][j]);
        }
    }
    cout<<s+dp[n][n]<<endl;
    return ;
}