BZOJ4727 [POI2017]Turysta 【竞赛图哈密顿路径/回路】

题目链接

BZOJ4727

题解

前置芝士

1.竞赛图存在哈密顿路径

2.竞赛图存在哈密顿回路，当且仅当它是强联通的

所以我们将图缩点后，拓扑排序后一定是一条链，且之前的块内的点和之后块内的点的边一定全都由前面指向后面

而每个块都是强联通的，所以我们从起点出发，一定能找到一条路径走完后面所有点

我们只需预处理出每个强联通块内的一条哈密顿回路，就可以求出答案了

现在问题转化成了求竞赛图的哈密顿回路

我们先求出一条哈密顿路径

哈密顿路径

从竞赛图中任意一个点出发向外扩展，维护一个链表

假若扩展到点\(u\)

1.如果\(u\)指向链头或链尾，直接加入链表

2.否则链的中间一定存在相邻两点，使得\(i\)指向\(u\)，\(u\)指向\(i + 1\)，这时候把\(u\)插入之间即可

哈密顿回路

我们在哈密顿路径的基础上构造哈密顿回路

首先如果存在如图情况，前\(4\)个点构成回路



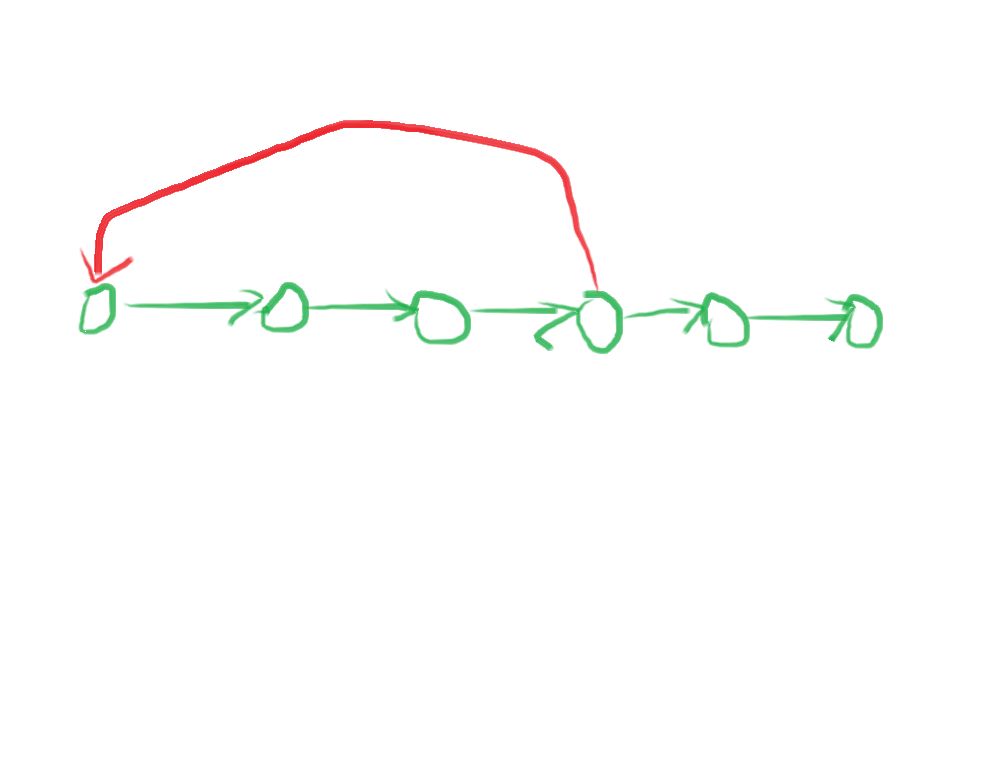
我们先找到最大的一个这样的回路，然后只需处理后面不在圈内的几个点

对于一个点\(u\)，如果存在一条\(u\)指向圈内点的边，那么\(u\)可以插入圈内

否则跳过\(u\)，将\(u\)和之后插入圈内的点一起插入圈内

由于图是强联通的，所以最后一定能全部加入

复杂度\(O(n^2)\)

#include<algorithm>
#include<iostream>
#include<cstdlib>
#include<cstring>
#include<cstdio>
#include<vector>
#include<queue>
#include<cmath>
#include<map>
#define LL long long int
#define REP(i,n) for (register int i = 1; i <= (n); i++)
#define cls(s,v) memset(s,v,sizeof(s))
#define mp(a,b) make_pair<int,int>(a,b)
#define cp pair<int,int>
#define res register
using namespace std;
const int maxn = 2005,maxm = 100005,INF = 0x3f3f3f3f;
inline int read(){
	int out = 0,flag = 1; char c = getchar();
	while (c < 48 || c > 57){if (c == '-') flag = 0; c = getchar();}
	while (c >= 48 && c <= 57){out = (out << 1) + (out << 3) + c - 48; c = getchar();}
	return flag ? out : -out;
}
int tmp[20],ti;
inline void write(int x){
	ti = 0;
	while (x) tmp[++ti] = x % 10,x /= 10;
	while (ti) putchar('0' + tmp[ti--]);
}
vector<int> S[maxn];
int n,G[maxn][maxn];
int dfn[maxn],low[maxn],Scc[maxn],st[maxn],top,cnt,scci;
int nxt[maxn],head[maxn],tail[maxn];
int Nxt[maxn],Head[maxn],Tail[maxn];
int g[maxn][maxn],de[maxn],q[maxn],hh,tt;
int tp[maxn],pos[maxn],ans[maxn],ansi,tot;
int c[maxn],ci;
void dfs(int u){
	dfn[u] = low[u] = ++cnt;
	st[++top] = u;
	for (res int to = 1; to <= n; to++){
		if (!G[u][to]) continue;
		if (!dfn[to]){
			dfs(to);
			low[u] = min(low[u],low[to]);
		}
		else if (!Scc[to]) low[u] = min(low[u],dfn[to]);
	}
	if (low[u] == dfn[u]){
		scci++;
		do{
			Scc[st[top]] = scci;
			S[scci].push_back(st[top]);
		}while (st[top--] != u);
	}
}
void workline(){
	int siz;
	for (res int p = 1; p <= scci; p++){
		siz = S[p].size();
		head[p] = tail[p] = S[p][0];
		for (res int i = 1; i < siz; i++){
			int u = S[p][i];
			if (G[u][head[p]]) nxt[u] = head[p],head[p] = u;
			else if (G[tail[p]][u]) nxt[tail[p]] = u,tail[p] = u;
			else for (res int j = head[p]; j; j = nxt[j])
				if (G[j][u] && G[u][nxt[j]]){
					nxt[u] = nxt[j]; nxt[j] = u; break;
				}
		}
	}
}
void workcir(){
	int p,last;
	for (int i = 1; i <= scci; i++){
		ci = 0; p = 1;
		for (int k = head[i]; k; k = nxt[k]) c[++ci] = k;
		for (int k = ci; k; k--)
			if (G[c[k]][head[i]]) {p = k; break;}
		Head[i] = c[1]; Tail[i] = c[p];
		for (int k = 1; k < p; k++) Nxt[c[k]] = c[k + 1];
		last = c[p + 1];
		for (int k = p + 1; k <= ci; k++){
			int u = c[k],flag = false;
			for (int j = Nxt[Head[i]],pre = Head[i]; j; j = Nxt[pre = j])
				if (G[u][j]){
					Nxt[pre] = last;
					Nxt[u] = j;
					flag = true;
					break;
				}
			if (flag) last = c[k + 1];
			else Nxt[u] = c[k + 1];
		}
		Nxt[Tail[i]] = Head[i];
	}
}
void work(){
	for (res int i = 1; i <= n; i++){
		int u = Scc[i];
		for (res int j = 1; j <= n; j++)
			if (G[i][j] && Scc[j] != u && !g[u][Scc[j]])
				de[Scc[j]]++,g[u][Scc[j]] = 1;
	}
	for (res int i = 1; i <= scci; i++) if (!de[i]) q[++tt] = i;
	int u; hh = 1;
	while (hh <= tt){
		u = q[hh++]; pos[u] = ++tot; tp[tot] = u;
		for (int i = 1; i <= scci; i++) if (g[u][i]){
			if (!(--de[i])) q[++tt] = i;
		}
	}
	for (res int u = 1; u <= n; u++){
		int s = Scc[u];
		ans[ansi = 1] = u;
		for (res int i = Nxt[u]; i != u; i = Nxt[i]) ans[++ansi] = i;
		for (res int j = pos[s] + 1; j <= scci; j++){
			int t = tp[j];
			ans[++ansi] = Head[t];
			for (res int i = Nxt[Head[t]]; i != Head[t]; i = Nxt[i])
				ans[++ansi] = i;
		}
		write(ansi); putchar(' ');
		for (res int i = 1; i <= ansi; i++){
			write(ans[i]);
			if (i < ansi) putchar(' ');
		}
		puts("");
	}
}
int main(){
	n = read();
	for (res int i = 2; i <= n; i++)
		for (res int j = 1; j < i; j++)
			G[i][j] = ((G[j][i] = read()) ^ 1);
	REP(i,n) if (!dfn[i]) dfs(i);
	workline();
	//puts("LXT");
	workcir();
	//puts("LXT");
	work();
	return 0;
}