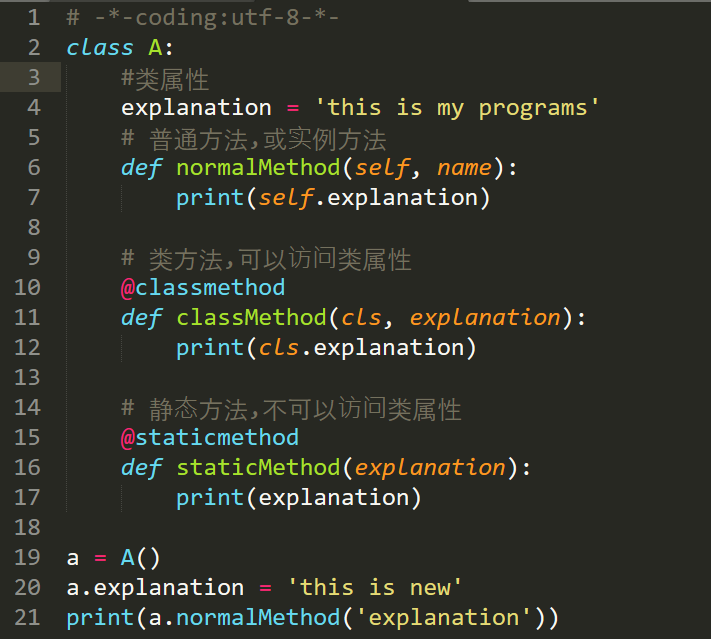
首先形式上的区别，实例方法隐含的参数为类实例self，而类方法隐含的参数为类本身cls。 静态方法无隐含参数，主要为了类实例也可以直接调用静态方法。

　　所以逻辑上，类方法被类调用，实例方法被实例调用，静态方法两者都能调用。主要区别在于参数传递上的区别，实例方法悄悄传递的是self引用作为参数，而类方法悄悄传递的是cls引用作为参数。

接下来看用类和实例分别能否调用类属性

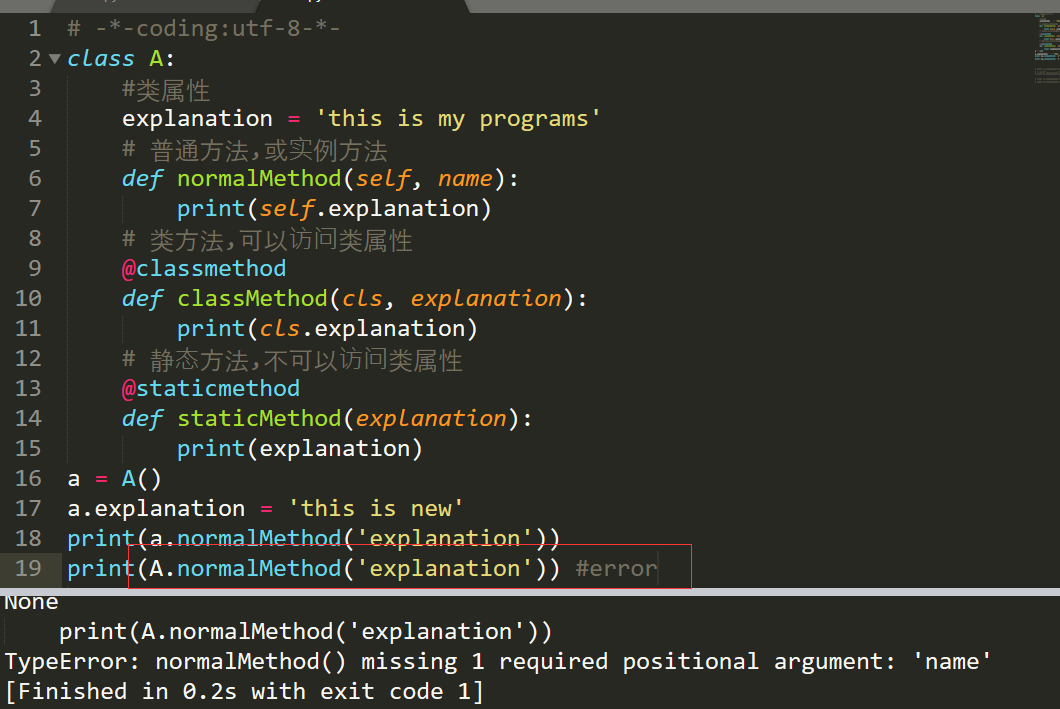
故  实例方法（普通方法）应该由实例调用，类不能调用；

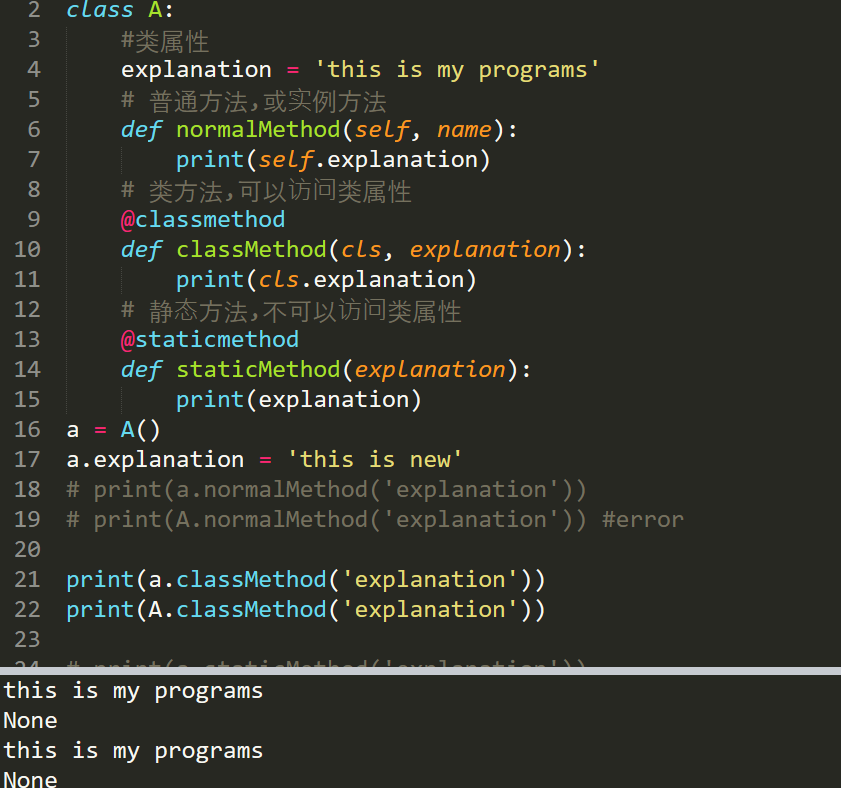
类方法可以由类调用，而且因为传入了参数cls，故也可以由实例来调用。

静态方法两者都能调用

总结成一张表就是：

注意类实例方法调用的结果和静态方法调用的结果的区别：

实例方法（普通方法）——————————————————————随着实例属性的改变而改变

类方法（无论是类调用还是实例调用）———————————————都是类属性的值，不随实例属性的变化而变化

静态方法————————————————————————————不可以访问类属性，故直接输出传入方法的值

一文详解python的类方法，普通方法和静态方法的更多相关文章

  1. 详解Python中的__init__和__new__(静态方法)

    一.__init__ 方法是什么? 使用Python写过面向对象的代码的同学,可能对 __init__ 方法已经非常熟悉了,__init__ 方法通常用在初始化一个类实例的时候.例如: #-*- co ...

  2. 详解Python编程中基本的数学计算使用

    详解Python编程中基本的数学计算使用 在Python中,对数的规定比较简单,基本在小学数学水平即可理解. 那么,做为零基础学习这,也就从计算小学数学题目开始吧.因为从这里开始,数学的基础知识列位肯 ...

  3. 详解python的装饰器decorator

    装饰器本质上是一个python函数,它可以让其它函数在不需要任何代码改动的情况下增加额外的功能. 装饰器的返回值也是一个函数对象.它经常用于有切面需求的场景,比如:插入日志,性能测试,事务处理,缓存, ...

  4. 详解 Python 的二元算术运算，为什么说减法只是语法糖？

    原题 | Unravelling binary arithmetic operations in Python 作者 | Brett Cannon 译者 | 豌豆花下猫("Python猫&q ...

  5. 举例详解Python中的split()函数的使用方法

    这篇文章主要介绍了举例详解Python中的split()函数的使用方法,split()函数的使用是Python学习当中的基础知识,通常用于将字符串切片并转换为列表,需要的朋友可以参考下   函数:sp ...

  6. 详解Python中re.sub--转载

    [背景] Python中的正则表达式方面的功能,很强大. 其中就包括re.sub,实现正则的替换. 功能很强大,所以导致用法稍微有点复杂. 所以当遇到稍微复杂的用法时候,就容易犯错. 所以此处,总结一 ...

  7. 详解Python模块导入方法

    python常被昵称为胶水语言,它能很轻松的把用其他语言制作的各种模块(尤其是C/C++)轻松联结在一起.python包含子目录中的模块方法比较简单,关键是能够在sys.path里面找到通向模块文件的 ...

  8. 详解python函数的参数

    详解python函数的参数 一.参数的定义 1.函数的参数在哪里定义 在python中定义函数的时候,函数名后面的括号里就是用来定义参数的,如果有多个参数的话,那么参数之间直接用逗号, 隔开 案列: ...

  9. 详解Python函数参数定义及传参（必备参数、关键字参数、默认可省略参数、可变不定长参数、*args、**kwargs）

    详解Python函数参数定义及传参(必备参数.关键字参数.默认可省略参数.可变不定长参数.*args.**kwargs) Python函数参数传参的种类   Python中函数参数定义及调用函数时传参 ...

随机推荐

  1. Fibonacci number

    https://github.com/Premiumlab/Python-for-Algorithms--Data-Structures--and-Interviews/blob/master/Moc ...

  2. 2018.07.01洛谷P2617 Dynamic Rankings（带修主席树）

    P2617 Dynamic Rankings 题目描述 给定一个含有n个数的序列a[1],a[2],a[3]--a[n],程序必须回答这样的询问:对于给定的i,j,k,在a[i],a[i+1],a[i ...

  3. hdu-1150（二分图+匈牙利算法）

    题目链接:http://acm.hdu.edu.cn/showproblem.php?pid=1150 思路:题目中给出两个机器A,B:给出k个任务,每个任务可以由A的x状态或者B的y状态来完成. 完 ...

  4. 25. Green Living 绿色生活

    25. Green Living 绿色生活 ①We all know that humans are damaging the environment,but what can we do about ...

  5. noip第10课作业

    1.     统计不同类型字符出现次数 [问题描述] 输入一个字符串(假设长度不超过1000个字符),统计其中大写,小写,数字,其他字符出现的次数. [样例输入]Hello,what are you ...

  6. 深入理解BS结构应用程序

    随着学习的深入,和编程经验的丰富,对BS应用程序有一些认识. 在一些讨论软件技术的QQ群里,或一些社区.BBS中,经常会有一些初学者会犯一些认知性的错误.比如经常会有一些朋友提这样的一些问题:“我怎么 ...

  7. 来回最短路POJ3268

    这个题得主要考点在于给你的图是去了再回来得有向图,如何模块化解决呢就是转变图的方向,我们根据初始得放心求出每个点到x得最短路,然后转变所有路得方向再求出所有点到x得最短路,最后一相加就是最后的来回了~ ...

  8. spring boot搭建Hello Word

    一.安装与配置jdk 二.安装与配置maven 安装好maven,必须配置环境变量 通过cmd命令查询maven是否安装成功,以下是安装成功的界面 修改setting.xml的配置,制定本地仓库的路径 ...

  9. Mono For Android 之 配置环境

    下载 Xamarin Mono For Android 4.6.07004 完整离线破解版 (包括除 Android SDK 外的所有文件) Android SDK. 资源源自 http://www. ...

  10. MVC4 项目开发日志（1）

    最近一直在定义一个功能全面,层次结构分明的框架.一边学习一边应用.