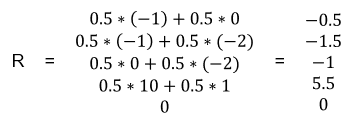MDP中值函数的求解
MDP概述
马尔科夫决策过程(Markov Decision Process)是强化学习(reinforcement learning)最基本的模型框架。它对序列化的决策过程做了很多限制。比如状态\(S_t\)和动作\(a_t\)只有有限个、\((S_t,a_t)\)对应的回报\(R_t\)是给定的、状态转移只依赖于当前状态\(S_t\)而与之前的状态\(S_{t-1},S_{t-2},...\)无关等等。 当给定一个MDP具体问题,常常需要计算在当前策略\(\pi\)之下,每个状态的值函数的值。而自己真正计算的时候,又不知怎么计算,这里给出一个具体的计算值函数的例子。分别用矩阵运算和方程组求解两种方式给出。
MDP问题设置
如图所示(来源:UCL Course on RL)
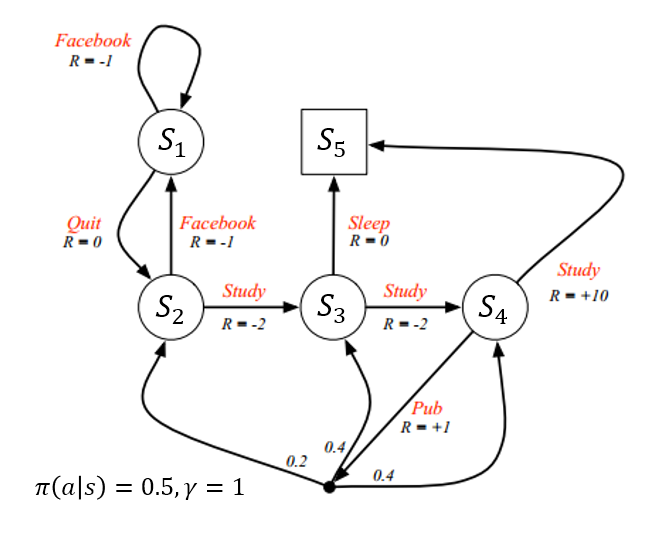
该例子可以理解为一个学生的生活状态,在不同的状态,他可以选择学习、睡觉、发文章等等动作,同时获得相应的回报\(R\)(reward)。
- 其中状态空间为{\(S_1,S_2,...,S_5\)},动作空间为{刷Facebook,睡觉,学习,发表文章,弃疗}。
- 每个状态有两个可选动作(\(S_5\)为终止状态),每个动作被选择的概率都为0.5,折扣因子\(\gamma=1\)。\((\pi(a|s)=0.5,\gamma=1\))
矩阵解法
据图可得如下转移概率矩阵P
化简可得
其中\(P_{11}=0.5\)即表示从状态\(S_1\)转移到状态\(S_1\)的概率为0.5,其他同理。
每个状态转移的平均reward可如下计算,例如\(R_{1}=P[Facebook|S_1]*R_{Facebook}+P[Quit|S_1]*R_{Quit}=0.5*(-1)+0.5*0=-0.5\)
则有R的向量如下
那么已知转移概率矩阵\(P\)和回报向量\(R\),利用贝尔曼方程,则可求得值函数的解\(v\)。贝尔曼方程可矩阵表示如下
\[
v = R +\gamma Pv
\]
- 则有
\[
v = R +\gamma Pv\\
(I-\gamma P)v = R\\
v = (I - \gamma P)^{-1}R
\]
其中\(\gamma=1\)
- 剩下的就只是矩阵运算。我们运用python numpy计算如下
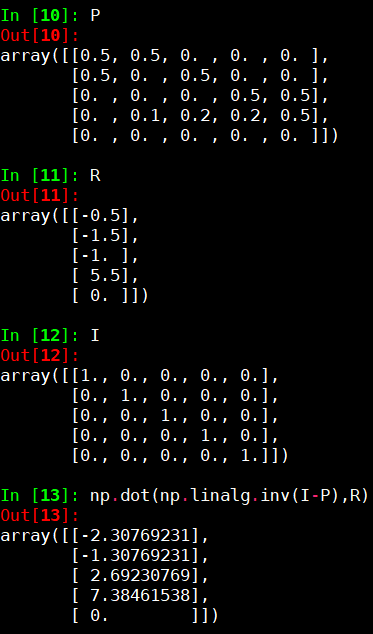
则可得
\[
\begin{array}{l}
v_1 \approx -2.3 \\
v_2 \approx -1.3 \\
v_3 \approx 2.7 \\
v_4 \approx 7.4 \\
v_5 = 0
\end{array}
\]
即为所求。
列方程组求解
矩阵运算表达和计算都很简便,但经常会忘记其缘由,为何可以这样求解。那么还可以回归最本质的解方程组的方式求解。即将所有的状态转移用方程的形式罗列出来,然后联立方程组求解即可。这种情况下,我们不必去记贝尔曼方程的矩阵表示形式,只需知道值函数的一步转移公式如下:
\[
v_{\pi}(s_t) = \sum_{a \in A}\pi(a|s_t)(R_{s_t}^a+\gamma\sum_{s_{t+1} \in S}P_{s_ts_{t+1}}^av_{\pi}(s_{t+1}))
\]
其中,\(\pi(a|s_t)\)表示在状态\(s_t\)下选择动作\(a\)的概率,\(R_{s_t}^a\)表示在状态\(s_t\)下选择动作\(a\)得到的回报,\(P_{s_ts_{t+1}}^a\)表示在状态\(s_t\)下选择动作\(a\)之后转移到状态\(s_{t+1}\)的概率(当前问题是确定性的马尔科夫链,选择固定的动作后就一定会转移到确定的状态,即\(P_{s_ts_{t+1}}^a=1\)),\(v_{\pi}(s_{t+1})\)表示状态\(s_{t+1}\)的值函数。这个式子看起来很麻烦,其实它想表达的就是,前一个状态的值函数等于它能转移到的所有下一状态的值函数和所采取的动作的回报的概率加权之和。
我们用状态\(S_1\)举例。
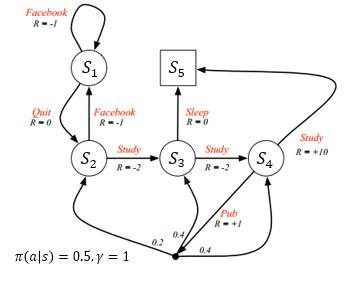
从图中可以看出,在\(S_1\)状态下,有两个动作可以选择:刷Facebook或者弃疗。两个动作的选取率都为0.5。刷Facebook的回报是-1,同时又转移到状态\(S_1\)。弃疗的回报是0,同时转移到状态\(S_2\)。也就是说,在状态\(S_1\)的时候,要么刷Facebook并转移到状态\(S_1\),要么弃疗并转移到状态\(S_2\)。用上面的数学表达式表示,即是
\[
v_{\pi}(S_1) = 0.5(-1+v_{\pi}(S_1))+0.5(0+v_{\pi}(S_2))
\]
对每个状态作同样的状态转移分析,则可求得状态值函数的方程组。这里将\(v_{\pi}(S_i)\)记为\(v_i\),得到如下方程组:
\[
\begin{array}{l}
v_1 = 0.5(-1+v_1)+0.5(0+v_2) \\
v_2 = 0.5(-1+v_1)+0.5(-2+v_3) \\
v_3 = 0.5(-2+v_4)+0.5(0+v_5) \\
v_4 = 0.5(10+v_5)+0.5(1+0.2v_2+0.4v_3+0.4v_4) \\
v_5 = 0
\end{array}
\]
化简有:
\[
\begin{array}{l}
v_1 = -1+v_2 \\
v_2 = -1.5+0.5v_1+0.5v_3 \\
v_3 = -1+0.5v_4 \\
8v_4 = 55+v_2+2v_3 \\
v_5 = 0
\end{array}
\]
求解方程组可得相同的结果:
\[
\begin{array}{l}
v_1 \approx -2.3 \\
v_2 \approx -1.3 \\
v_3 \approx 2.7 \\
v_4 \approx 7.4 \\
v_5 = 0
\end{array}
\]
注
需要注意,这里求解的MDP状态值函数,每个状态的回报(reward)是根据转移概率计算的平均回报,这称为贝尔曼期望方程(Bellman Expectation Equation)。而在强化学习中,通常是选取使得价值最大的动作执行,这种解法称为最优值函数(Optimal Value Function),得到的解不再是期望值函数,而是理论最大值函数。此时相当于策略\(\pi\)已经改变,且非线性,线性方程组不再适用,需要通过数值计算的方式求出。通常的做法是设置状态值函数\(v(s)\)和状态-动作值函数\(q(s,a)\)迭代求解。最终得到
\[
v^*(s)=\max\limits_{\pi}v_{\pi}(s)\\
q^*(s,a)=\max\limits_{\pi}q_{\pi}(s,a)
\]
其中通过\(q^*(s,a)\)选择动作即为最优策略\(\pi^*\):
\[
\pi^*(a|s)=
\left\{\begin{array}{l}
1,if \quad a=\arg\max\limits_{a \in A}q^*(s,a)\\
0,otherwise
\end{array}\right.
\]
这里只给出迭代求解的方程如下(Bellman Optimality Equation):
\[
v^*(s)=\max\limits_a(R_s^a+\gamma\sum_{s'\in S}P_{ss'}^av^*(s'))\\
q^*(s,a)=R_s^a+\gamma\sum_{s' \in S}P_{ss'}^a\max\limits_{a'}q^*(s',a')
\]
随机设置初始值,通过迭代计算,即可收敛到最优解。
MDP中值函数的求解的更多相关文章
- 强化学习中的无模型 基于值函数的 Q-Learning 和 Sarsa 学习
强化学习基础: 注: 在强化学习中 奖励函数和状态转移函数都是未知的,之所以有已知模型的强化学习解法是指使用采样估计的方式估计出奖励函数和状态转移函数,然后将强化学习问题转换为可以使用动态规划求解的 ...
- matlab中fmincon函数求解非线性规划问题
Matlab求解非线性规划,fmincon函数的用法总结 1.简介 在matlab中,fmincon函数可以求解带约束的非线性多变量函数(Constrained nonlinear multivari ...
- sqlserver中的表值函数和标量值函数
顾名思义:表值函数返回的是表,而标量值函数可以返回基类型 一.表值函数 用户定义表值函数返回 table 数据类型.对于内联表值函数,没有函数主体:表是单个 SELECT 语句的结果集. 以下示例创建 ...
- JS中给函数参数添加默认值
最近在Codewars上面看到一道很好的题目,要求用JS写一个函数defaultArguments,用来给指定的函数的某些参数添加默认值.举例来说就是: // foo函数有一个参数,名为x var f ...
- c++中带返回值函数没写return能通过编译但运行时会出现奇怪问题
c++中带返回值函数没写return能通过编译但运行时会出现奇怪问题 例如: string myFunc(){ theLogics(); } 发现调用: myFunc(); 崩溃. 但调用: cout ...
- eclipse 中main()函数中的String[] args如何使用?通过String[] args验证账号密码的登录类?静态的主方法怎样才能调用非static的方法——通过生成对象?在类中制作一个方法——能够修改对象的属性值?
eclipse 中main()函数中的String[] args如何使用? 右击你的项目,选择run as中选择 run configuration,选择arguments总的program argu ...
- JS中给函数参数添加默认值(多看课程)
JS中给函数参数添加默认值(多看课程) 一.总结 一句话总结:咋函数里面是可以很方便的获取调用函数的参数的,做个判断就好,应该有简便方法,看课程. 二.JS中给函数参数添加默认值 最近在Codewar ...
- P中值选址问题的整数规划求解
P中值选址问题的整数规划求解 一 .P-中值问题 p-中值选址问题是一个常见的选址问题. 问题是给定I个需求结点和J个待选设施地点, 要求选择p个地点建立设施, 使得运输成本最低. 下面是个英文的问题 ...
- C#中的函数(二) 有参有返回值的函数
接上一篇 C#中的函数(-) 无参无返回值的函数 http://www.cnblogs.com/fzxiaoyi/p/8502613.html 这次研究下C#中的函数(二) 有参有返回值的函数 依然写 ...
随机推荐
- centos无法通过ssh连接的解决
系统环境是centos7,虚拟机环境下的.在使用ssh工具连接虚拟机的时候发现连接不上,用的是root 先检查openssh-server是否安装: yum list installed | grep ...
- 在windows的IDEA运行Presto
After building Presto for the first time, you can load the project into your IDE and run the server. ...
- 浅谈iOS与社交化网络
CHENYILONG Blog 社交化网络 技术博客http://www.cnblogs.com/ChenYilong/ 新浪微博http://weibo.com/luohanchenyilong ...
- mac nginx 安装及PHP配置
安装nginx 1.安装brew命令 ruby -e "$(curl -fsSL https://raw.githubusercontent.com/Homebrew/install/mas ...
- Pythagorean Triples(Codeforces Round #368 (Div. 2) + 构建直角三角形)
题目链接: https://codeforces.com/contest/707/problem/C 题目: 题意: 告诉你直角三角形的一条边,要你输出另外两条边. 思路: 我们容易发现除2外的所有素 ...
- spfa+差分约束系统(D - POJ - 1201 && E - POJ - 1364&&G - POJ - 1)+建边的注意事项+超级源点的建立
题目链接:https://cn.vjudge.net/contest/276233#problem/D 具体大意: 给出n个闭合的整数区间[ai,bi]和n个整数c1,-,cn. 编写一个程序: 从标 ...
- 防止 Google Smart Lock 记忆错的用户名
默认 chrome 会查找密码上面的那个(非隐藏非禁用)的表单域 如果上面是个短信验证码框,就会将验证码当成用户名提示用户保存. 在用户名 input 上添加 autocomplete="u ...
- KL散度(Kullback–Leibler divergence)
KL散度是度量两个分布之间差异的函数.在各种变分方法中,都有它的身影. 转自:https://zhuanlan.zhihu.com/p/22464760 一维高斯分布的KL散度 多维高斯分布的KL散度 ...
- Linux嵌入式交叉编译环境 的搭建【转】
转自:http://blog.csdn.net/woaixiaozhe/article/details/7395435 1. 安装标准的C开发环境,由于Linux安装默认是不安装的,所以需要先安装一下 ...
- mvc 分部视图(Partial)显示登陆前后变化以及Shared文件夹在解决方案资源管理器中没有显示的问题
刚开始我的解决方案资源管理器中没有显示Shared文件夹,但Shared文件夹在项目中是实际存在的,我搜了下好像没有类似的解答(可能是我搜索的关键词不够准确).后来自己看了下vs2012. 其实解决方 ...