P2661 信息传递 二分图的最小环

　　

题目描述

有 nn 个同学（编号为 11 到 nn ）正在玩一个信息传递的游戏。在游戏里每人都有一个固定的信息传递对象，其中，编号为 ii 的同学的信息传递对象是编号为 T_iTi​ 的同学。

游戏开始时，每人都只知道自己的生日。之后每一轮中，所有人会同时将自己当前所知的生日信息告诉各自的信息传递对象（注意：可能有人可以从若干人那里获取信息， 但是每人只会把信息告诉一个人，即自己的信息传递对象）。当有人从别人口中得知自 己的生日时，游戏结束。请问该游戏一共可以进行几轮？

输入输出格式

输入格式：

共22行。

第11行包含1个正整数 nn ，表示 nn 个人。

第22行包含 nn 个用空格隔开的正整数 T_1,T_2,\cdots\cdots,T_nT1​,T2​,⋯⋯,Tn​ ，其中第 ii 个整数 T_iTi​ 表示编号为 ii 的同学的信息传递对象是编号为 T_iTi​ 的同学， T_i \leq nTi​≤n 且 T_i \neq iTi​≠i 。

输出格式：

11个整数，表示游戏一共可以进行多少轮。

输入输出样例

输入样例#1： 复制

5
2 4 2 3 1

输出样例#1： 复制

3

说明

样例1解释

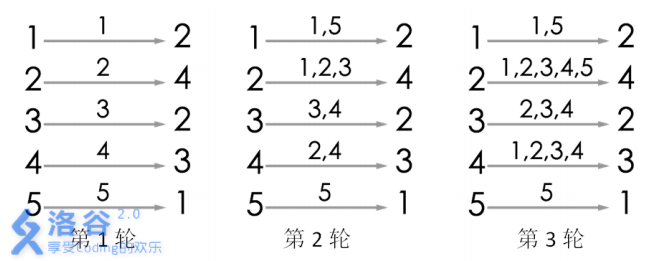
游戏的流程如图所示。当进行完第33 轮游戏后， 44号玩家会听到 22 号玩家告诉他自己的生日，所以答案为 33。当然，第 33 轮游戏后，22号玩家、 33 号玩家都能从自己的消息来源得知自己的生日，同样符合游戏结束的条件。

对于 30\%30%的数据， n ≤ 200n≤200；

对于 60\%60%的数据， n ≤ 2500n≤2500；

对于100\%100%的数据， n ≤ 200000n≤200000。

拓扑排序可以求是否有环   但是我不会求最小环

dfs 200000肯定会超时

可以采用拓扑排序优化 +dfs

300ms蒟蒻代码：

#include<bits/stdc++.h>
using namespace std;
//input b y bxd
#define rep(i,a,b) for(int i=(a);i<=(b);i++)
#define repp(i,a,b) for(int i=(a);i>=(b);--i)
#define RI(n) scanf("%d",&(n))
#define RII(n,m) scanf("%d%d",&n,&m)
#define RIII(n,m,k) scanf("%d%d%d",&n,&m,&k)
#define RS(s) scanf("%s",s);
#define ll long long
#define REP(i,N)  for(int i=0;i<(N);i++)
#define CLR(A,v)  memset(A,v,sizeof A)
#define inf 0x3f3f3f3f
//////////////////////////////////
#define N  200000+9
int in[N];
vector<int>edge[N];
int vis[N];
int minn;
void dfs(int x,int cnt,int flag)
{
     vis[x]=;
     int k=edge[x][];
        vis[k]=;
        if(k==flag)
        {
           minn=min(minn,cnt);
           return ;
        }
        dfs(k,cnt+,flag);
}

int main()
{
        int n;
        RI(n);
        rep(i,,n)
        {
            int a,b;
            RI(a);
            in[a]++;
            edge[i].push_back(a);
        }
        queue<int>q;
        rep(i,,n)
        if(!in[i])q.push(i);//后来还要取出来 所以这里cnt不用变
        int cnt=;//计算入读为0的点
        while(!q.empty())
        {
            int u=q.front();q.pop();
            vis[u]=;//去掉不成环的点
            cnt++;
            if(edge[u].size())
            rep(i,,edge[u].size()-)
            {
                int v=edge[u][i];
                in[v]--;
                if(in[v]==)q.push(v);
            }
        }
        minn=inf;

        rep(i,,n)
        if(!vis[i])
            dfs(i,,i);

        cout<<minn;

    return ;
}

70ms

不要开队列!!!太慢了   只是借用拓扑排序的思想就够了

#include<bits/stdc++.h>
using namespace std;
//input b y bxd
#define rep(i,a,b) for(int i=(a);i<=(b);i++)
#define repp(i,a,b) for(int i=(a);i>=(b);--i)
#define RI(n) scanf("%d",&(n))
#define RII(n,m) scanf("%d%d",&n,&m)
#define RIII(n,m,k) scanf("%d%d%d",&n,&m,&k)
#define RS(s) scanf("%s",s);
#define ll long long
#define REP(i,N)  for(int i=0;i<(N);i++)
#define CLR(A,v)  memset(A,v,sizeof A)
#define inf 0x3f3f3f3f
//////////////////////////////////
#define N  200000+9
int in[N];
int edge[N];
int vis[N];
int minn;
void dfs(int x,int cnt,int flag)
{
     vis[x]=;
     int k=edge[x];
        if(k==flag)
        {
           minn=min(minn,cnt);
           return ;
        }
        dfs(k,cnt+,flag);
}
void del(int x)
{
    vis[x]=;
    if( --in[edge[x]]== )
        del(edge[x]);
}
int main()
{
        int n;
        RI(n);
        rep(i,,n)
        {
            int a,b;
            RI(a);
            in[a]++;
            edge[i]=a;
        }
        rep(i,,n)
        if(!in[i]&&!vis[i])
            del(i);

        minn=inf;
        rep(i,,n)
        if(!vis[i])
            dfs(i,,i);

        cout<<minn;
    return ;
}

并查集 70ms

和今天写的带权并查集

一个原理

#include<bits/stdc++.h>
using namespace std;
//input b y bxd
#define rep(i,a,b) for(int i=(a);i<=(b);i++)
#define repp(i,a,b) for(int i=(a);i>=(b);--i)
#define RI(n) scanf("%d",&(n))
#define RII(n,m) scanf("%d%d",&n,&m)
#define RIII(n,m,k) scanf("%d%d%d",&n,&m,&k)
#define RS(s) scanf("%s",s);
#define ll long long
#define REP(i,N)  for(int i=0;i<(N);i++)
#define CLR(A,v)  memset(A,v,sizeof A)
#define inf 0x3f3f3f3f
//////////////////////////////////
#define N  200000+9
int f[N];
int dis[N];//维护距离头的距离
int minn;
int find1(int x)
{
    if(x==f[x])return x;
    int k=find1(f[x]);
    dis[x]+=dis[f[x]];//这个只是回溯 传递 并不是改权值
    return f[x]=k;
}
void union1(int a,int b)
{
    int x=find1(a);
    int y=find1(b);
    if(x==y)
        minn=min(minn,dis[a]+dis[b]+);
    else
    {
        f[x]=y;
        dis[a]=dis[b]+;//这里为改权值
    }
}
int main()
{
    int n;
    RI(n);
    rep(i,,n)
    f[i]=i,dis[i]=;
    minn=inf;
    rep(i,,n)
    {
        int a;
        RI(a);
        union1(i,a);
    }
    cout<<minn;
}