【XSY1762】染色问题 网络流

题目描述

　　给定一张\(n\)个点\(m\)条边的无向图。每个顶点有一个颜色，要么是黑，要么是白。我们想进行一些操作，使得最终每一条边的两个端点都是不同的颜色。每一次操作，你可以将一条边的两个端点交换颜色。求最少的操作次数和具体的操作方式。

　　\(n\leq 500\)

题解

　　首先黑白染色，假设要让染出来的黑点最终成为黑点，那么

　　　1.对于原来的每个黑点\(i\)，连边\((S,i,1,0)\)

　　　2.对于染出来的每个黑点\(i\)，连边\((i,T,1,0)\)

　　　3.对于原图中的每条边\((u,v)\)，连边\((u,v,\infty,1),(v,u,\infty,1)\)，表示交换两个端点的花费。

　　跑完费用流后，每次bfs找到一条从\(S\)到\(T\)的路径，通过某些方法交换第一个点和最后一个点。

　　对于一条长度大于\(1\)的路径，第一个点一定是白色的，最后一个点一定是黑色的。（第一个点靠\(T\)，最后一个点靠\(S\)）

　　

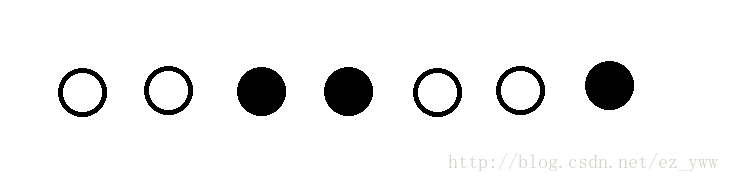
　　先把这个序列切成很多段，每段只有最右边的点是黑色的。

　　

　　把每段的黑点调到最前面

　　

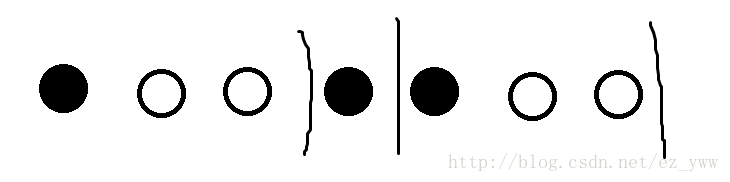
　　再从后往前交换每段的第一个点和前一段的最后一个点。

　　

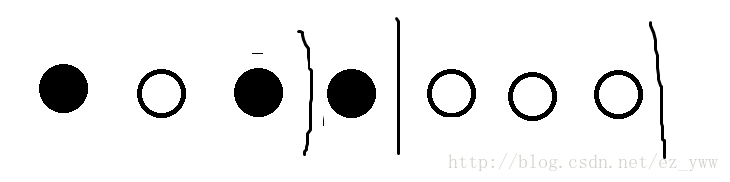
　　这样可以用长度\(-1\)步内交换第一个点和最后一个点。

　　时间复杂度：\(O(???)\)

代码

#include<cstdio>
#include<cstring>
#include<algorithm>
#include<cstdlib>
#include<ctime>
#include<utility>
#include<queue>
#include<list>
#include<vector>
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
typedef pair<int,int> pii;
queue<int> q;
//vector<pii> a;
int ax[1000010];
int ay[1000010];
int len=0;
struct li
{
	int h[510];
	int v[100010];
	int t[100010];
	int n;
	li()
	{
		memset(h,0,sizeof h);
		n=0;
	}
	void add(int x,int y)
	{
		n++;
		v[n]=y;
		t[n]=h[x];
		h[x]=n;
	}
};
li l;
struct graph
{
	int h[510];
	int u[500010];
	int v[500010];
	int w[500010];
	int c[500010];
	int t[500010];
	int p[500010];
	int n;
	void clear()
	{
		n=0;
		memset(h,0,sizeof h);
	}
	void add(int x,int y,int z,int d)
	{
		n++;
		u[n]=x;
		v[n]=y;
		w[n]=d;
		c[n]=z;
		p[n]=0;
		t[n]=h[x];
		h[x]=n;
	}
	int S,T;
	int gd[510];
	int gb[510];
	int gf[510];
	int flow,cost;
	int f[510];
	int op(int x)
	{
		return ((x-1)^1)+1;
	}
	int spfa()
	{
		memset(gd,0x7f,sizeof gd);
		gd[S]=0;
		gf[S]=0;
		q.push(S);
		int i,x;
		while(!q.empty())
		{
			x=q.front();
			q.pop();
			gb[x]=0;
			if(gd[x]>=gd[T])
				continue;
			for(i=h[x];i;i=t[i])
				if(c[i]&&gd[v[i]]>gd[x]+w[i])
				{
					gd[v[i]]=gd[x]+w[i];
					gf[v[i]]=i;
					if(!gb[v[i]])
					{
						gb[v[i]]=1;
						q.push(v[i]);
					}
				}
		}
		if(gd[T]==0x7f7f7f7f)
			return 0;
		flow++;
		cost+=gd[T];
		for(i=gf[T];i;i=gf[u[i]])
		{
			c[i]--;
			p[i]++;
			c[op(i)]++;
			p[op(i)]--;
		}
		return 1;
	}
	int maxflow()
	{
		flow=cost=0;
		while(spfa());
		return cost;
	}
	int p1[500010];
	int p2[500010];
	void check()
	{
		memset(gb,0,sizeof gb);
		gb[S]=1;
		gf[S]=0;
		q.push(S);
		int i;
		while(!q.empty())
		{
			int x=q.front();
			q.pop();
			for(i=h[x];i;i=t[i])
				if(p[i]&&!gb[v[i]])
				{
					gb[v[i]]=1;
					gf[v[i]]=i;
					if(v[i]==T)
					{
						while(!q.empty())
							q.pop();
						return;
					}
					q.push(v[i]);
				}
		}
	}
	void getans()
	{
		check();
		int i;
		int t1=0,t2=0;
		for(i=gf[T];i;i=gf[u[i]])
		{
			if(v[i]!=T)
				p1[++t1]=v[i];
			p[i]--;
		}
		for(i=t1;i>=2;i--)
			if(f[p1[i-1]])
				p2[++t2]=i;
			else
			{
//				a.push_back(pii(p1[i-1],p1[i]));
				ax[++len]=p1[i-1];
				ay[len]=p1[i];
				swap(f[p1[i]],f[p1[i-1]]);
			}
		for(i=t2;i>=1;i--)
		{
//			a.push_back(pii(p1[p2[i]],p1[p2[i]-1]));
			ax[++len]=p1[p2[i]];
			ay[len]=p1[p2[i]-1];
			swap(f[p1[p2[i]]],f[p1[p2[i]-1]]);
		}
	}
};
graph g1,g2;
char s[510];
int c[510];
int from[510][510];
int d[510][510];
int vis[100010];
int s1,s2;
int b,w;
int ans;
list<int> e,e1,e2;
void failed()
{
	printf("-1\n");
	exit(0);
}
void dfs(int x,int p)
{
	if(~vis[x])
	{
		if(vis[x]!=p)
			failed();
		return;
	}
	e.push_back(x);
	vis[x]=p;
	if(c[x])
		b++;
	else
		w++;
	if(p)
	{
		s1++;
		e1.push_back(x);
	}
	else
	{
		s2++;
		e2.push_back(x);
	}
	int i;
	for(i=l.h[x];i;i=l.t[i])
		dfs(l.v[i],p^1);
}
int build1()
{
	for(auto v1:e)
	{
		int i;
		for(i=l.h[v1];i;i=l.t[i])
		{
			int v2=l.v[i];
			g1.add(v1,v2,1000,1);
			g1.add(v2,v1,0,-1);
			g1.add(v2,v1,1000,1);
			g1.add(v1,v2,0,-1);
		}
		if(c[v1])
		{
			g1.add(g1.S,v1,1,0);
			g1.add(v1,g1.S,0,0);
		}
	}
	for(auto v1:e2)
	{
		g1.add(v1,g1.T,1,0);
		g1.add(g1.T,v1,0,0);
	}
	return g1.maxflow();
}
int build2()
{
	for(auto v1:e)
	{
		int i;
		for(i=l.h[v1];i;i=l.t[i])
		{
			int v2=l.v[i];
			g2.add(v1,v2,1000,1);
			g2.add(v2,v1,0,-1);
			g2.add(v2,v1,1000,1);
			g2.add(v1,v2,0,-1);
		}
		if(c[v1])
		{
			g2.add(g2.S,v1,1,0);
			g2.add(v1,g2.S,0,0);
		}
	}
	for(auto v1:e1)
	{
		g2.add(v1,g2.T,1,0);
		g2.add(g2.T,v1,0,0);
	}
	return g2.maxflow();
}
void rd(int &s)
{
	int c;
	while((c=getchar())<'0'||c>'9');
	s=c-'0';
	while((c=getchar())>='0'&&c<='9')
		s=s*10+c-'0';
}
int main()
{
	int n,m;
//	scanf("%d%d",&n,&m);
	rd(n);
	rd(m);
	int i;
	scanf("%s",s+1);
	for(i=1;i<=n;i++)
		c[i]=s[i]-'0';
	int x,y;
	for(i=1;i<=m;i++)
	{
//		scanf("%d%d",&x,&y);
		rd(x);
		rd(y);
		l.add(x,y);
		l.add(y,x);
	}
	memset(vis,-1,sizeof vis);
	ans=0;
	g1.S=g2.S=n+1;
	g1.T=g2.T=n+2;
	for(i=1;i<=n;i++)
		if(vis[i]==-1)
		{
			w=b=s1=s2=0;
			e.clear();
			e1.clear();
			e2.clear();
			dfs(i,0);
			if(w!=s1&&w!=s2)
				failed();
			int ans1=0x7fffffff,ans2=0x7fffffff;
			g1.clear();
			g2.clear();
			int f1,f2;
			if(w==s1&&b==s2)
			{
				ans1=build1();
				f1=g1.flow;
			}
			if(b==s1&&w==s2)
			{
				ans2=build2();
				f2=g2.flow;
			}
			if(ans1<ans2)
			{
				ans+=ans1;
				memcpy(g1.f,c,sizeof c);
				while(f1--)
					g1.getans();
			}
			else
			{
				ans+=ans2;
				memcpy(g2.f,c,sizeof c);
				while(f2--)
					g2.getans();
			}
		}
	printf("%d\n",ans);
//	for(auto v:a)
//		printf("%d %d\n",v.first,v.second);
	for(i=1;i<=len;i++)
		printf("%d %d\n",ax[i],ay[i]);
	return 0;
}