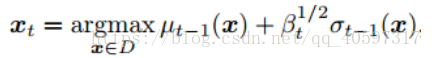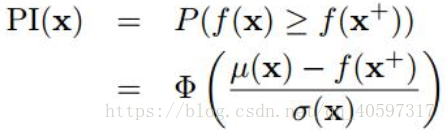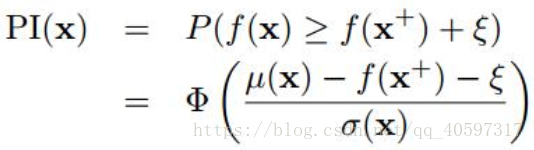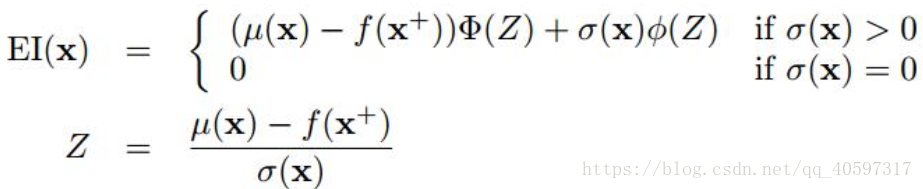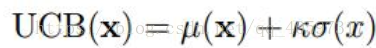贝叶斯优化 Bayesian Optimization
关键字:提取函数aquisition function,熵,响应曲面
简介:所谓优化,实际上就是一个求极值的过程,数据科学的很多时候就是求极值的问题。那么怎么求极值呢?很显然,很容易想到求导数,这是一个好方法,但是求导即基于梯度的优化的条件是函数形式已知才能求出导数,并且函数要是凸函数才可以。然而实际上很多时候是不满足这两个条件的,所以不能用梯度优化,贝叶斯优化应运而生了。
贝叶斯优化常原来解决反演问题,
(反演问题是指由结果及某些一般原理(或模型)出发去确定表征问题特征的参数(或模型参数))
贝叶斯优化的好处在于只需要不断取样,来推测函数的最大值。并且采样的点也不多。
一、贝叶斯优化的适用条件
不知道函数的具体形态即表达式
但是如果给定一个x,可以计算y。这里的计算方法可以使用之前的GPR,如果(x,y)够多了,那么就基本知道函数图像的走势了。
适用于小于20维的空间上优化
二、目的
找出函数的最值,这是最主要的目的。因为很多时候数据科学的一大部分问题都是做非线性函数f(x)的在范围A内的优化,或者简 单的说,求最大值/最小值。比如需要确定拟合的参数,可以求出关于参数的代价函数,求得该代价函数的最小值就可以确定 对应的最优参数了。那么求这个最小值就需要贝叶斯优化了。
大致知道函数长什么样子:与响应曲面相比,贝叶斯只知道最后函数大概什么走向,但是不知道自变量与因变量的关系。可以大致理解为构建响应曲面(虽然响应曲面努力拟合自变量与因变量的关系,下面是关于响应曲面)
响应曲面设计是利用合理的试验设计方法并通过实验得到一定数据,采用多元二次回归方程来拟合与响应值之间的函数关系,通过对回归方程的分析来寻求最优工艺参数,解决多变量问题的一种统计方法。
将响应看作是因素的函数,使用图形技术体现这种函数。一般假设指标和因素之间的关系可以用线性模型表示,即使用多元线性回归的方法。考虑m个因素和n个结果之间的关系,经常使用最小二乘法(就是我们数学上的曲线拟合。注意网页的线性最小二乘法的那一项,很重要。)
对于超定方程组,引入残差平方和函数
三、思路
1.因为GP可以得到在一个新的点x的后验概率P(f(x)|x,D),这里的D为数据集,所以如果想求得极值,可以从GP计算出的x点的均值和方差考虑。可以根据该后验概率的一些指标确定下一个我应该取哪一个点,才有较大的概率尽快的达到极值。
2.如何选取下一个点:求提取函数u达到极值对应的x。这就是上一条的所谓指标。
3.基本算法
可以看出,这里就是不断的求max(AF)对应的点Xt,计算Xt的Yt,即取样,加到数据集。周而复始的循环。
原谅我写的X,Y都是大写,否则x和t一样大了,强迫症发作
关于D,D中的数据周围的方差都较小,也就是我们对他们周围的点了解较多,所以只要有足够多的数据到D里面,那么就会收敛到f(x)
4.Xt的选取
5.优化方向
explore 探索未知的空间,尽可能的探索未知的空间,这样对f(x)的后验概率才会更接近f(x)
exploit,强化已有的结果,在现有最大值的附近进行探索,保证找到的f(x)会更大
6.常用的AF
6.1 probability of improvement(POI)
目的:新的采样能提升最大值的概率最大
表达式为:MPI(maximum probability of improvement),或P算法
Φ(·) 表示的是正态累计分布函数
改进:这里的参数为trade-off系数,可以控制倾向explore还是exploit
这里倾向于局部搜索
6.2 Expected improvement(EI)
可以在explore和explot之间平衡,explore时选择均值大的点,exploit选择方差大的点
参数通常选0.01
6.3 Upper confidence bound
直接比较置信区间的最大值,效果非常好
参考:http://blog.sina.com.cn/s/blog_76d02ce90102xqs6.html
贝叶斯优化 Bayesian Optimization的更多相关文章
- 贝叶斯优化(Bayesian Optimization)深入理解
目前在研究Automated Machine Learning,其中有一个子领域是实现网络超参数自动化搜索,而常见的搜索方法有Grid Search.Random Search以及贝叶斯优化搜索.前两 ...
- 贝叶斯优化(Bayesian Optimization)只需要看这一篇就够了,算法到python实现
贝叶斯优化 (BayesianOptimization) 1 问题提出 神经网咯是有许多超参数决定的,例如网络深度,学习率,正则等等.如何寻找最好的超参数组合,是一个老人靠经验,新人靠运气的任务. 穷 ...
- 基于贝叶斯优化的超参数tuning
https://arimo.com/data-science/2016/bayesian-optimization-hyperparameter-tuning/ 贝叶斯优化:使用高斯过程作为代理函数, ...
- DeepMind提出新型超参数最优化方法:性能超越手动调参和贝叶斯优化
DeepMind提出新型超参数最优化方法:性能超越手动调参和贝叶斯优化 2017年11月29日 06:40:37 机器之心V 阅读数 2183 版权声明:本文为博主原创文章,遵循CC 4.0 BY ...
- 朴素贝叶斯(Naive Bayesian)
简介 Naive Bayesian算法 也叫朴素贝叶斯算法(或者称为傻瓜式贝叶斯分类) 朴素(傻瓜):特征条件独立假设 贝叶斯:基于贝叶斯定理 这个算法确实十分朴素(傻瓜),属于监督学习,它是一个常用 ...
- 调参贝叶斯优化(BayesianOptimization)
from sklearn.datasets import make_classification from sklearn.model_selection import cross_val_score ...
- (ZT)算法杂货铺——分类算法之贝叶斯网络(Bayesian networks)
https://www.cnblogs.com/leoo2sk/archive/2010/09/18/bayes-network.html 2.1.摘要 在上一篇文章中我们讨论了朴素贝叶斯分类.朴素贝 ...
- 条件独立(conditional independence) 结合贝叶斯网络(Bayesian network) 概率有向图 (PRML8.2总结)
本文会利用到上篇,博客的分解定理,需要的可以查找上篇博客 D-separation对任何用有向图表示的概率模型都成立,无论随机变量是离散还是连续,还是两者的结合. 部分图为手写,由于本人字很丑,望见谅 ...
- 条件独立(conditional independence) 结合贝叶斯网络(Bayesian network) 概率有向图 (PRML8.2总结)
转:http://www.cnblogs.com/Dzhouqi/p/3204481.html本文会利用到上篇,博客的分解定理,需要的可以查找上篇博客 D-separation对任何用有向图表示的概率 ...
随机推荐
- OAuth2.0的四种授权模式
1.什么是OAuth2 OAuth(开放授权)是一个开放标准,允许用户授权第三方移动应用访问他们存储在另外的服务提供者上的信息,而不需要将用户名和密码提供给第三方移动应用或分享他们数据的所有内容,OA ...
- k8s Ipvs 内部网络自动分配和内部网络一致ip地址,导致ip冲突
[链接]Linux负载均衡--LVS(IPVS)https://www.jianshu.com/p/36880b085265 [链接]kube-proxyipvsmodecreateunnecessa ...
- Flutter移动电商实战 --(37)路由_Fluro引入和商品详细页建立
https://github.com/theyakka/fluro pages/details_page.dart新建页面 使用路由 先添加路由插件的引用 fluro: ^1.4.0 如果网络上下载不 ...
- Flutter移动电商实战 --(14)首页_拨打电话操作
拨打电话的功能在app里也很常见,比如一般的外卖app都会有这个才做.其实Flutter本身是没给我们提供拨打电话的能力的,那我们如何来拨打电话那? 1.编写店长电话模块 这个小伙伴们一定轻车熟路了, ...
- Servlet的入门案例
编写入门案例 1)编写java类,继承HttpServlet类 2)重新doGet和doPost方法 3)Servlet程序交给tomcat服务器运行!! 3.1 servlet程序的class码拷贝 ...
- Tomcat发布项目
WEB项目的目录结构 演示动态项目的创建 把项目打包成war包: 进入这个项目中,使用命令: jar cvf aaa.war * 发布动态项目的三种方式: 1. 直接复制项目到webapps下 2. ...
- 008-多线程-锁-JUC锁-CyclicBarrier【让一组线程到达一个屏障(也可以叫同步点)时被阻塞,直到最后一个线程到达屏障时,屏障才会开门,所有被屏障拦截的线程才会继续运行】
一.概述 “循环栅栏”.大概的意思就是一个可循环利用的屏障. CyclicBarrier是一个同步辅助类,允许一组线程互相等待,直到到达某个公共屏障点 (common barrier point).因 ...
- Build Telemetry for Distributed Services之OpenCensus:C#
OpenCensus Easily collect telemetry like metrics and distributed traces from your services OpenCensu ...
- ios 本地模糊搜索
/* 手机 选择区域 模型 */ #import <Foundation/Foundation.h> NS_ASSUME_NONNULL_BEGIN @interface MYSelect ...
- MATLAB常用快捷键总结
MATLAB 命令栏显示处理的常用命令 清屏:clc 紧凑显示格式:format compact 宽松显示格式:format loose 数据高精度显示:format longG 数据低精度显示:fo ...