【CodeForces】915 G. Coprime Arrays 莫比乌斯反演,前缀和，差分

Coprime Arrays

CodeForces - 915G

Let's call an array a of size n coprime iff gcd(a1, a2, ..., a**n) = 1, where gcd is the greatest common divisor of the arguments.

You are given two numbers n and k. For each i (1 ≤ i ≤ k) you have to determine the number of coprime arrays a of size n such that for every j (1 ≤ j ≤ n) 1 ≤ a**j ≤ i. Since the answers can be very large, you have to calculate them modulo 109 + 7.

Input

The first line contains two integers n and k (1 ≤ n, k ≤ 2·106) — the size of the desired arrays and the maximum upper bound on elements, respectively.

Output

Since printing 2·106 numbers may take a lot of time, you have to output the answer in such a way:

Let b**i be the number of coprime arrays with elements in range [1, i], taken modulo 109 + 7. You have to print , taken modulo 109 + 7. Here denotes bitwise xor operation (^ in C++ or Java, xor in Pascal).

Examples

Input

3 4

Output

82

Input

2000000 8

Output

339310063

Note

Explanation of the example:

Since the number of coprime arrays is large, we will list the arrays that are non-coprime, but contain only elements in range [1, i]:

For i = 1, the only array is coprime. b1 = 1.

For i = 2, array [2, 2, 2] is not coprime. b2 = 7.

For i = 3, arrays [2, 2, 2] and [3, 3, 3] are not coprime. b3 = 25.

For i = 4, arrays [2, 2, 2], [3, 3, 3], [2, 2, 4], [2, 4, 2], [2, 4, 4], [4, 2, 2], [4, 2, 4], [4, 4, 2] and [4, 4, 4] are not coprime. b4 = 55.

题意：

给你一个整数n和k，

问你长度为n的整数数组中，每一个元素a[i] 要求满足\(a[i]<=k\)，即最大值为k

b[i] = 最大值为i（即数组中每一个元素\(a[j]<=i\)），满足条件的数组种类个数。

让你输出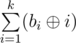

思路：

根据莫比乌斯反演，可以得到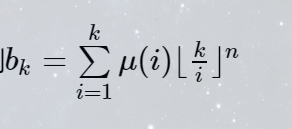

但是我们需要求的是b1到bk而不是单独的一个bi，这是最重要的一个性质。

所以我们考虑\(b[i+1]\)和\(b[i]\)的关系，

\(b[i+1]=Σ[d|k] μ(d)*((k/d)^n-(k/d-1)^n)+b[i]\)

然后差分，求\(f[i]=b[i+1]-b[i]\)

计算答案的时候求一个前缀和即可，

记得\(i^n\) 要预处理出来降低时间复杂度。

代码：

#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <cmath>
#include <queue>
#include <stack>
#include <map>
#include <set>
#include <vector>
#include <iomanip>
#define ALL(x) (x).begin(), (x).end()
#define sz(a) int(a.size())
#define rep(i,x,n) for(int i=x;i<n;i++)
#define repd(i,x,n) for(int i=x;i<=n;i++)
#define pii pair<int,int>
#define pll pair<long long ,long long>
#define gbtb ios::sync_with_stdio(false),cin.tie(0),cout.tie(0)
#define MS0(X) memset((X), 0, sizeof((X)))
#define MSC0(X) memset((X), '\0', sizeof((X)))
#define pb push_back
#define mp make_pair
#define fi first
#define se second
#define eps 1e-6
#define gg(x) getInt(&x)
#define chu(x) cout<<"["<<#x<<" "<<(x)<<"]"<<endl
#define du3(a,b,c) scanf("%d %d %d",&(a),&(b),&(c))
#define du2(a,b) scanf("%d %d",&(a),&(b))
#define du1(a) scanf("%d",&(a));
using namespace std;
typedef long long ll;
ll gcd(ll a, ll b) {return b ? gcd(b, a % b) : a;}
ll lcm(ll a, ll b) {return a / gcd(a, b) * b;}
ll powmod(ll a, ll b, ll MOD) {a %= MOD; if (a == 0ll) {return 0ll;} ll ans = 1; while (b) {if (b & 1) {ans = ans * a % MOD;} a = a * a % MOD; b >>= 1;} return ans;}
void Pv(const vector<int> &V) {int Len = sz(V); for (int i = 0; i < Len; ++i) {printf("%d", V[i] ); if (i != Len - 1) {printf(" ");} else {printf("\n");}}}
void Pvl(const vector<ll> &V) {int Len = sz(V); for (int i = 0; i < Len; ++i) {printf("%lld", V[i] ); if (i != Len - 1) {printf(" ");} else {printf("\n");}}}

inline void getInt(int *p);
const int maxn = 2000010;
const int inf = 0x3f3f3f3f;
/*** TEMPLATE CODE * * STARTS HERE ***/
#define N maxn
bool vis[N];
long long prim[N], mu[N], sum[N], cnt;
void get_mu(long long n)
{
    mu[1] = 1;
    for (long long i = 2; i <= n; i++) {
        if (!vis[i]) {mu[i] = -1; prim[++cnt] = i;}
        for (long long j = 1; j <= cnt && i * prim[j] <= n; j++) {
            vis[i * prim[j]] = 1;
            if (i % prim[j] == 0) { break; }
            else { mu[i * prim[j]] = -mu[i]; }
        }
    }
    for (long long i = 1; i <= n; i++) { sum[i] = sum[i - 1] + mu[i]; }
}
ll n, k;
ll b[maxn];
const ll mod = 1e9 + 7ll;
ll f[maxn];
int main()
{
    //freopen("D:\\code\\text\\input.txt","r",stdin);
    //freopen("D:\\code\\text\\output.txt","w",stdout);
    get_mu(maxn - 1);
    cin >> n >> k;
    cout<<mu[2]<<endl;
    repd(i, 0, k) {
        ll cnt = powmod(1ll * i, n, mod);
        b[i] = cnt;
    }
    ll ans = 0ll;
    ll ANS = 0ll;
    repd(i, 1, k) {
        for (int j = i; j <= k; j += i) {
            f[j] += mu[i] * (b[j / i] - b[j / i - 1]) % mod;
            f[j] = (f[j] + mod) % mod;
        }
//        chu(f[i]);
        ans = (ans + (f[i] )) % mod;
        ANS = (ANS + (ans ^ i)) % mod;
    }
    cout << ANS << endl;
    return 0;
}

inline void getInt(int *p)
{
    char ch;
    do {
        ch = getchar();
    } while (ch == ' ' || ch == '\n');
    if (ch == '-') {
        *p = -(getchar() - '0');
        while ((ch = getchar()) >= '0' && ch <= '9') {
            *p = *p * 10 - ch + '0';
        }
    } else {
        *p = ch - '0';
        while ((ch = getchar()) >= '0' && ch <= '9') {
            *p = *p * 10 + ch - '0';
        }
    }
}