Graphic系统综合练习案例-绘制饼状图

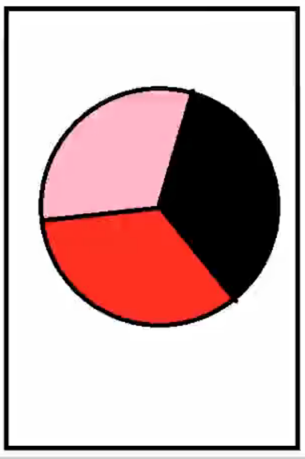
这里用一个案例来将之前学过的关于绘制相关的东东加强巩固一下，纯绘制，木有加点击效果，先来看下最终效果：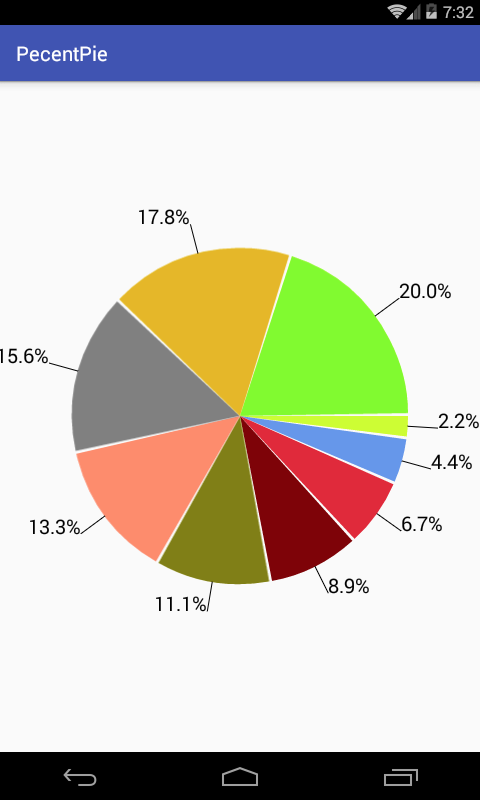

github中这种百分比饼图的效果非常非常之多，实际在项目中开发当产品有这样类似的需求时做为开发着的我们第一想法可能就是先去找开源的，然后基于开源的进行适当修改修改就变成自己的了，但是往往去修改开源的项目是比较费时的，而如果不了解其原理可能折腾半天最终发现还不如自己从头继承View按自己的思路来实现，所以有必要自己从头到尾一点点去实现类似的效果，当然上面的效果是比较一般的，重在综合练习，巩固基础，从图上可以看出主要是练习：圆弧的绘制、线的绘制、文字的绘制，话不多说下面看下怎么一点点去实现它：

饼状图的数据处理

对于这个百分比饼图的数据源应该是动态由用户决定的，所以首先将数据进行封装一下，如下：

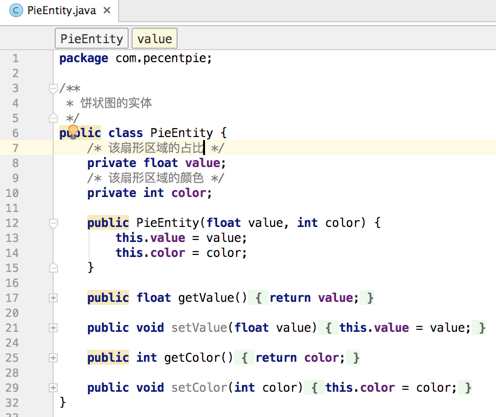
然后搭建基础框架，新建一个自定义View类：

将其声明在布局文件中：

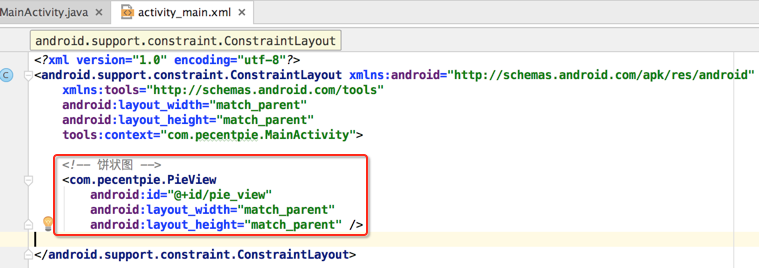
在Activity中使用View:

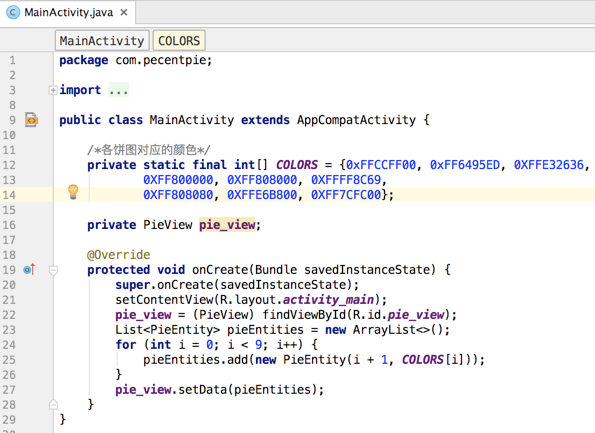
扇形的外接矩形的处理

在正式绘制之前，先来做一个分析：

而要绘制这个圆，实际上它是绘制在如下外切矩形之内的：

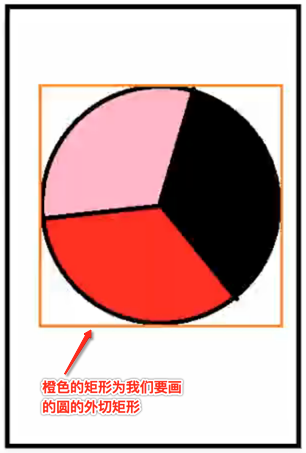
所以在正式绘制扇形之前首先得计算一下外接矩形的左上右下位置，但是有一个关键步骤需要首先去做，那就是关于绘制坐标系的问题，如下：

但是，这样计算这个外接矩形的坐标就比较麻烦，有没有简便一点的办法呢？可以将绘制坐标做如下移动：

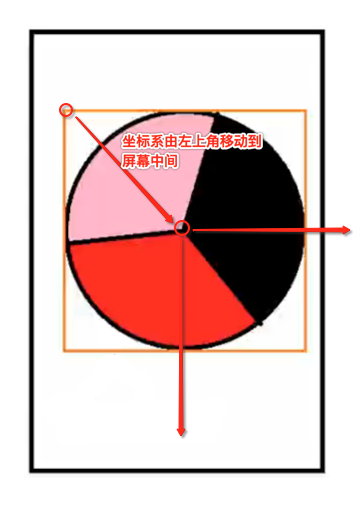
那这样做的好处？好处大大滴，如下：

所以下面首先来将坐标移动到屏幕的中心，而由于我们自定义View在布局文件中的声明是：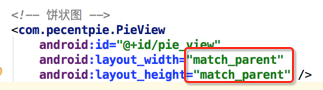

那View中如何知道该控件的大小呢？这里学习一个新的api：

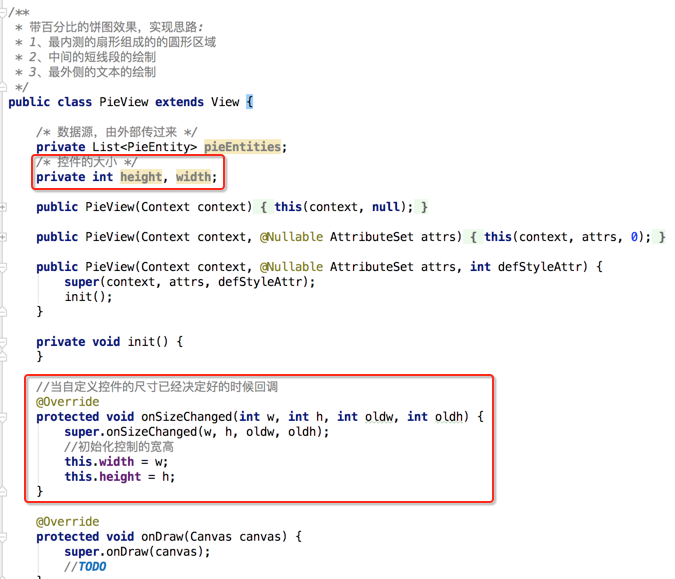
有了宽高之后，则可以移动绘制的坐标系了，这时就用到了之前学的api了：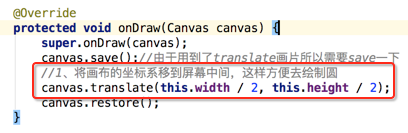

接下来就是来计算我们要绘制的圆的半径了【因为只要确定了半径我们的矩形位置就可能确定了】，为了让圆刚好显示在屏幕上，应该这样来确定圆的半径：

1、首先取屏幕宽高的最少值；

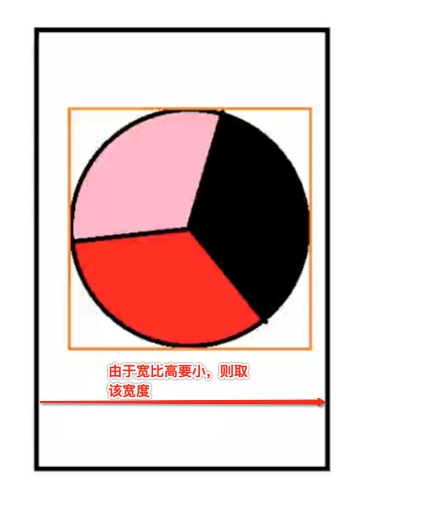
对应代码：

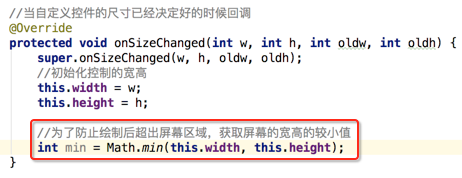
2、确定圆的直径：在最少值中为了让其圆左右有一些间隙已变之后能有空间去在圆上绘制文本，则应该只取其长度的7成；

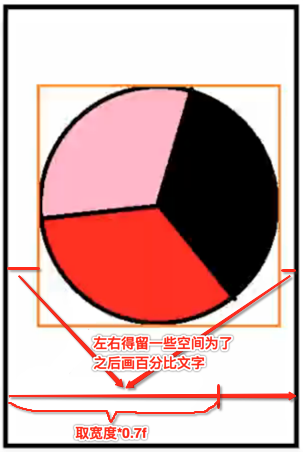
3、基于直径/2得到半径；

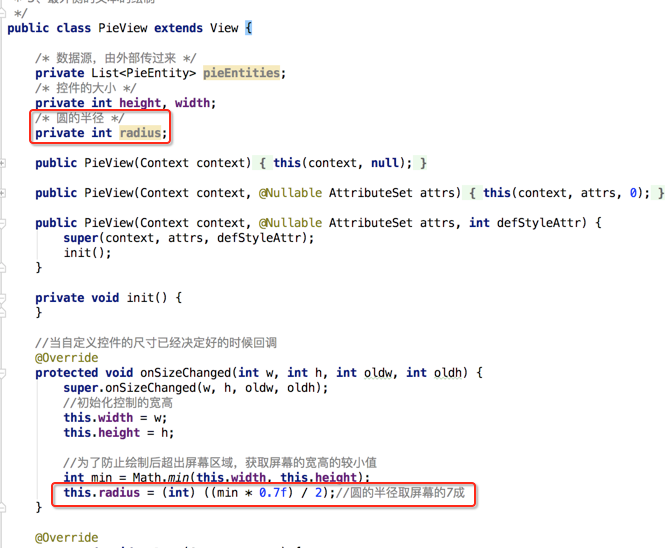
这时就可以定义外接矩形的坐标了：

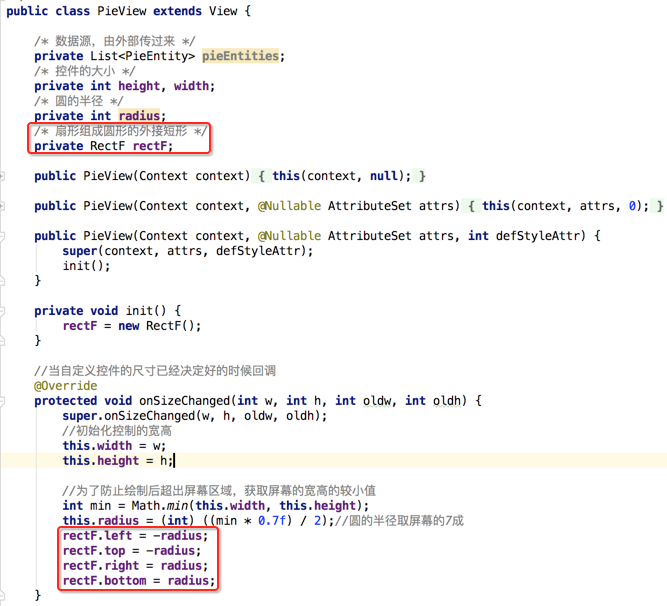
扇形的绘制处理

有了外接矩形接着就开始扇形的绘制了，首先需要遍历数据一个个进行绘制，如下：

首先设置一下扇形的颜色，当然就需要用到Paint对象啦：

public class PieView extends View {

    /* 数据源，由外部传过来 */
    private List<PieEntity> pieEntities;
    /* 控件的大小 */
    private int height, width;
    /* 圆的半径 */
    private int radius;
    /* 扇形组成圆形的外接短形 */
    private RectF rectF;
    /* 绘制扇形的画笔 */
    private Paint paint;

    public PieView(Context context) {
        this(context, null);
    }

    public PieView(Context context, @Nullable AttributeSet attrs) {
        this(context, attrs, 0);
    }

    public PieView(Context context, @Nullable AttributeSet attrs, int defStyleAttr) {
        super(context, attrs, defStyleAttr);
        init();
    }

    private void init() {
        rectF = new RectF();

        paint = new Paint();
        paint.setAntiAlias(true);
    }

    //当自定义控件的尺寸已经决定好的时候回调
    @Override
    protected void onSizeChanged(int w, int h, int oldw, int oldh) {
        super.onSizeChanged(w, h, oldw, oldh);
        //初始化控制的宽高
        this.width = w;
        this.height = h;

        //为了防止绘制后超出屏幕区域，获取屏幕的宽高的较小值
        int min = Math.min(this.width, this.height);
        this.radius = (int) ((min * 0.7f) / 2);//圆的半径取屏幕的7成
        rectF.left = -radius;
        rectF.top = -radius;
        rectF.right = radius;
        rectF.bottom = radius;
    }

    @Override
    protected void onDraw(Canvas canvas) {
        super.onDraw(canvas);
        canvas.save();//由于用到了translate画片所以需要save一下
        //1、将画布的坐标系移到屏幕中间，这样方便去绘制圆
        canvas.translate(this.width / 2, this.height / 2);
        //2、绘制扇形
        drawPie(canvas);
        canvas.restore();
    }

    private void drawPie(Canvas canvas) {
        for (int i = 0; i < pieEntities.size(); i++) {
            PieEntity pieEntity = pieEntities.get(i);
            paint.setColor(pieEntity.getColor());//设置扇形的颜色
        }
    }

    /**
     * 设置饼图的源数据
     */
    public void setData(List<PieEntity> pieEntities) {
        this.pieEntities = pieEntities;
    }
}

接下来绘制扇形，具体如何绘制扇形这个在当时画人脸已经有说过绘制一个弧【http://www.cnblogs.com/webor2006/p/7341697.html】，这里需要用到Path了，而具体会用到Path中的这个方法：

而startAngle和sweepAngle这俩参数还是未知的，在正式调用绘制扇形之前先来解决这两个参数：

startAngle:这个默认从0度开始，所以先声明：

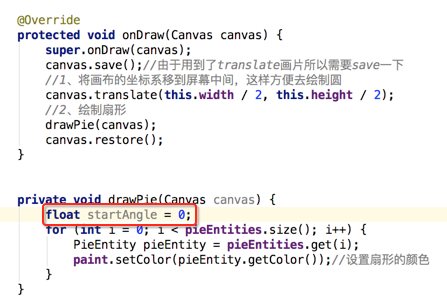
但是每次循环之后，起始角度则为当前扇形的终点角度，如下：

而一个扇形的结束角度是需要知道sweepAngle才能得到它，公式是：startAngle+sweepAngle，所以下面看下sweepAngle怎么计算。

sweepAngle:每个扇形的角度由应该为：当前扇形的比例（当前扇形数据中的值/整个数据值的总数） * 360度，而当前扇形数据中的值为：

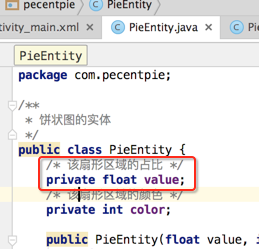
而整个数据值的总和则应该进么数据遍历得到：

public class PieView extends View {

    /* 数据源，由外部传过来 */
    private List<PieEntity> pieEntities;
    /* 控件的大小 */
    private int height, width;
    /* 圆的半径 */
    private int radius;
    /* 扇形组成圆形的外接短形 */
    private RectF rectF;
    /* 绘制扇形的画笔 */
    private Paint paint;
    /* 总占比 */
    private int totalValue;

    public PieView(Context context) {
        this(context, null);
    }

    public PieView(Context context, @Nullable AttributeSet attrs) {
        this(context, attrs, 0);
    }

    public PieView(Context context, @Nullable AttributeSet attrs, int defStyleAttr) {
        super(context, attrs, defStyleAttr);
        init();
    }

    private void init() {
        rectF = new RectF();

        paint = new Paint();
        paint.setAntiAlias(true);
    }

    //当自定义控件的尺寸已经决定好的时候回调
    @Override
    protected void onSizeChanged(int w, int h, int oldw, int oldh) {
        super.onSizeChanged(w, h, oldw, oldh);
        //初始化控制的宽高
        this.width = w;
        this.height = h;

        //为了防止绘制后超出屏幕区域，获取屏幕的宽高的较小值
        int min = Math.min(this.width, this.height);
        this.radius = (int) ((min * 0.7f) / 2);//圆的半径取屏幕的7成
        rectF.left = -radius;
        rectF.top = -radius;
        rectF.right = radius;
        rectF.bottom = radius;
    }

    @Override
    protected void onDraw(Canvas canvas) {
        super.onDraw(canvas);
        canvas.save();//由于用到了translate画片所以需要save一下
        //1、将画布的坐标系移到屏幕中间，这样方便去绘制圆
        canvas.translate(this.width / 2, this.height / 2);
        //2、绘制扇形
        drawPie(canvas);
        canvas.restore();
    }

    private void drawPie(Canvas canvas) {
        float startAngle = 0;
        for (int i = 0; i < pieEntities.size(); i++) {
            PieEntity pieEntity = pieEntities.get(i);
            paint.setColor(pieEntity.getColor());//设置扇形的颜色
        }
    }

    /**
     * 设置饼图的源数据
     */
    public void setData(List<PieEntity> pieEntities) {
        this.pieEntities = pieEntities;
        for (PieEntity pieEntity : pieEntities) {
            this.totalValue += pieEntity.getValue();
        }
    }
}

再回到绘制方法来计算sweepAngle的值为：

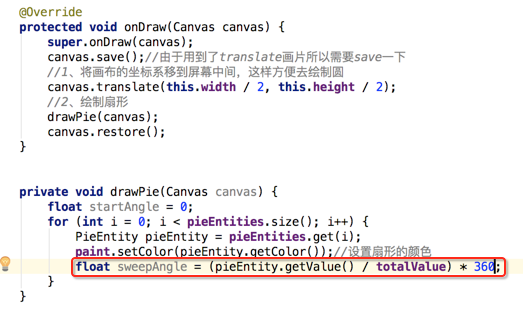
这时startAngle和sweepAngle参数值都确定了，下面则可以进式进行扇形的绘制了：

public class PieView extends View {

    /* 数据源，由外部传过来 */
    private List<PieEntity> pieEntities;
    /* 控件的大小 */
    private int height, width;
    /* 圆的半径 */
    private int radius;
    /* 扇形组成圆形的外接短形 */
    private RectF rectF;
    /* 绘制扇形的画笔 */
    private Paint paint;
    /* 总占比 */
    private int totalValue;
    private Path path;

    public PieView(Context context) {
        this(context, null);
    }

    public PieView(Context context, @Nullable AttributeSet attrs) {
        this(context, attrs, 0);
    }

    public PieView(Context context, @Nullable AttributeSet attrs, int defStyleAttr) {
        super(context, attrs, defStyleAttr);
        init();
    }

    private void init() {
        rectF = new RectF();

        paint = new Paint();
        paint.setAntiAlias(true);

        path = new Path();
    }

    //当自定义控件的尺寸已经决定好的时候回调
    @Override
    protected void onSizeChanged(int w, int h, int oldw, int oldh) {
        super.onSizeChanged(w, h, oldw, oldh);
        //初始化控制的宽高
        this.width = w;
        this.height = h;

        //为了防止绘制后超出屏幕区域，获取屏幕的宽高的较小值
        int min = Math.min(this.width, this.height);
        this.radius = (int) ((min * 0.7f) / 2);//圆的半径取屏幕的7成
        rectF.left = -radius;
        rectF.top = -radius;
        rectF.right = radius;
        rectF.bottom = radius;
    }

    @Override
    protected void onDraw(Canvas canvas) {
        super.onDraw(canvas);
        canvas.save();//由于用到了translate画片所以需要save一下
        //1、将画布的坐标系移到屏幕中间，这样方便去绘制圆
        canvas.translate(this.width / 2, this.height / 2);
        //2、绘制扇形
        drawPie(canvas);
        canvas.restore();
    }

    private void drawPie(Canvas canvas) {
        float startAngle = 0;
        for (int i = 0; i < pieEntities.size(); i++) {
            PieEntity pieEntity = pieEntities.get(i);
            paint.setColor(pieEntity.getColor());//设置扇形的颜色
            float sweepAngle = (pieEntity.getValue() / totalValue) * 360;
            path.arcTo(rectF, startAngle, sweepAngle);
            canvas.drawPath(path, paint);
        }
    }

    /**
     * 设置饼图的源数据
     */
    public void setData(List<PieEntity> pieEntities) {
        this.pieEntities = pieEntities;
        for (PieEntity pieEntity : pieEntities) {
            this.totalValue += pieEntity.getValue();
        }
    }
}

但是startAngle在每次循环之后都需要进行改变，所以不要忘了去更改它的值：

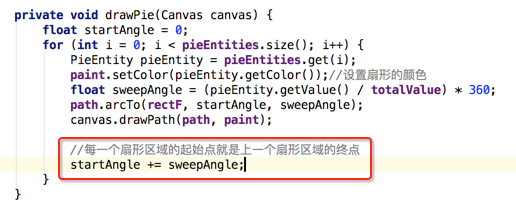
下面开始运行看下效果：

咦~咋回事不是每个扇形都定义的不同的颜色了么，为啥都是同一个颜色呢，而且该绿色为我们定义的第一个颜色：

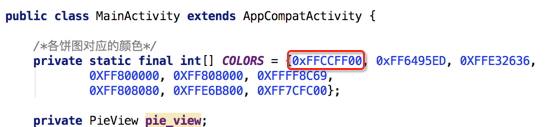
这里需要引入另外一个关于Path的API，下面直接写出：

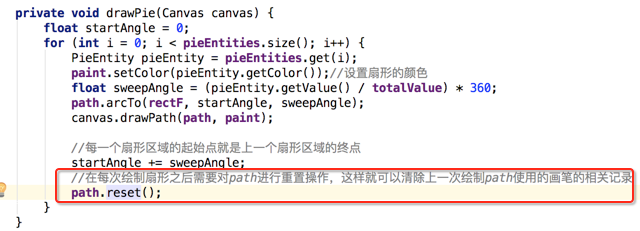
那为什么要用它呢？因为path会记录上一次绘制的颜色，所以说这个一定得注意！！！下面再看一下效果：

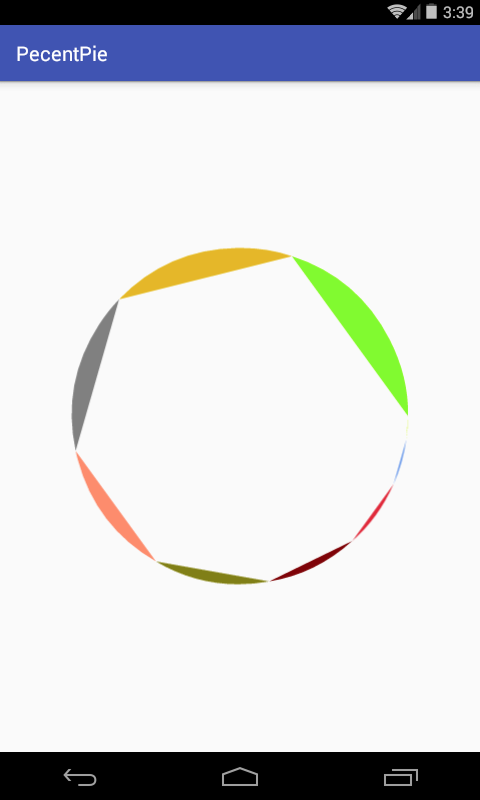
呃，怎么还是有问题，这是由于我们在绘制Path时需要设置它的绘制坐标点，应该是(0,0)的位置，也就是每次都是从圆心进行绘制：

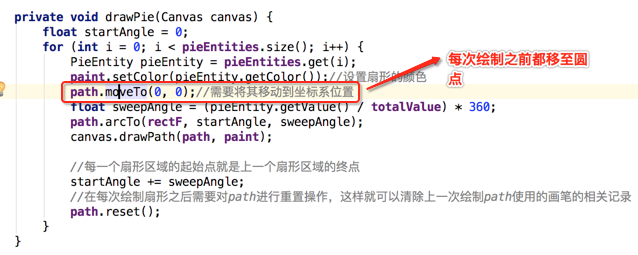
再次看效果：

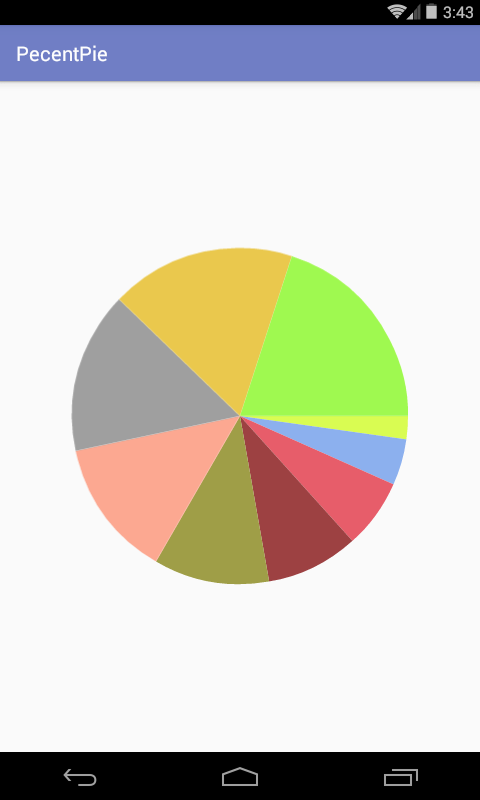
OK,效果终于出来了，但是！！！对比最终效果来看：

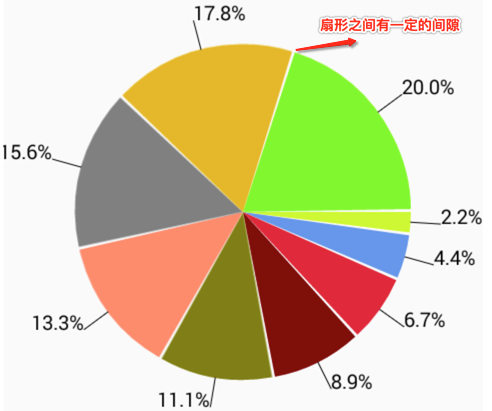
那如何达到这样的效果呢？其实思路很简单，如下：

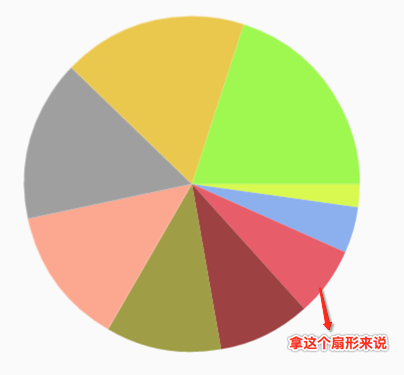
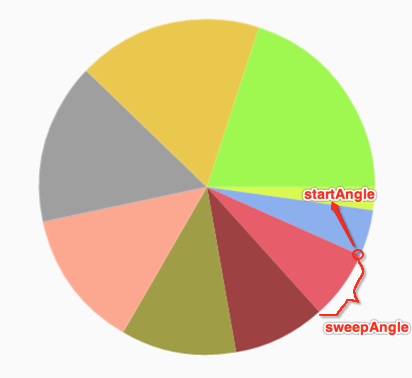
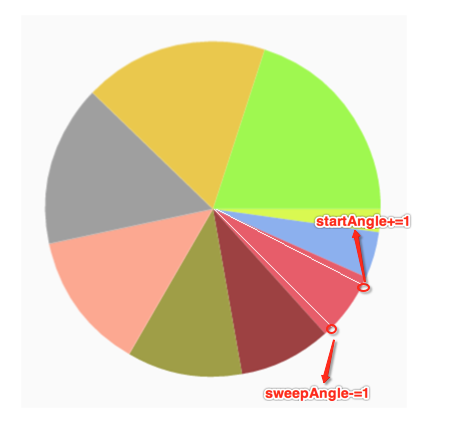
于是乎说干就干：

看下效果：

直线的绘制处理

接下来处理各个扇形上的直线绘制了，先看一下最终效果：

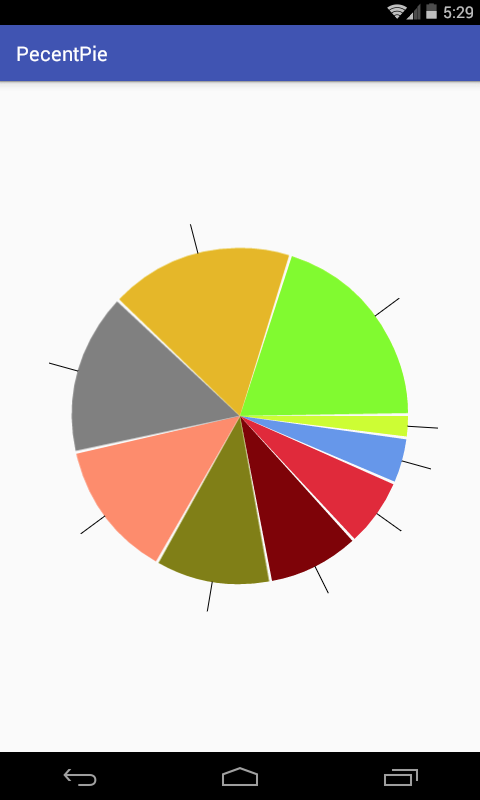
先来分析一下该直线的需求，先看下草图：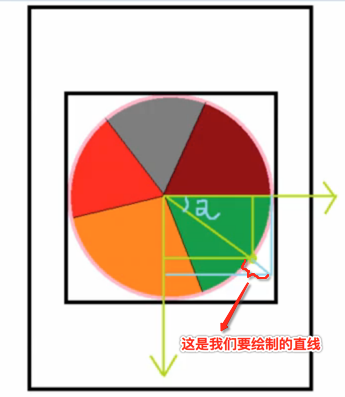

要求一：绘制直线的反向延长线经过圆心。

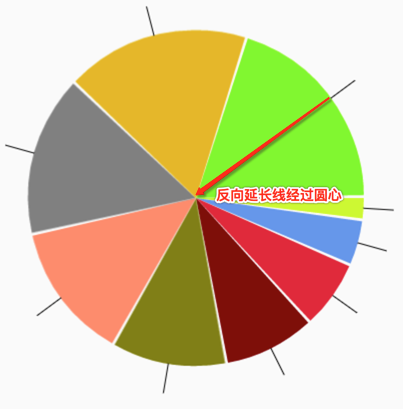
要求二：直线与圆的交点在对应扇形的中点处。

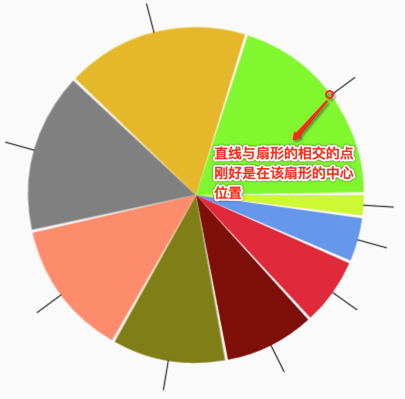
要求三：所有的直线的颜色一致，而不像扇形每块颜色不一样。

清求了需求之后，那想想如何去实现这种规则的直线呢？继续分析：

根据"两点成一线"原则，我们只要计算出来这两点那就好办了，如下：

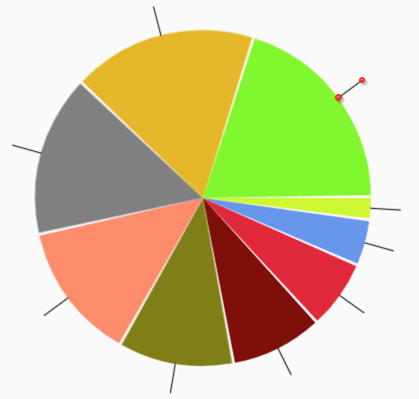
而计算这两点需要用到我们在高中学习的三角函数的计算的知识，先来回顾一下，如今早已忘得差不多了，百度百科一下：

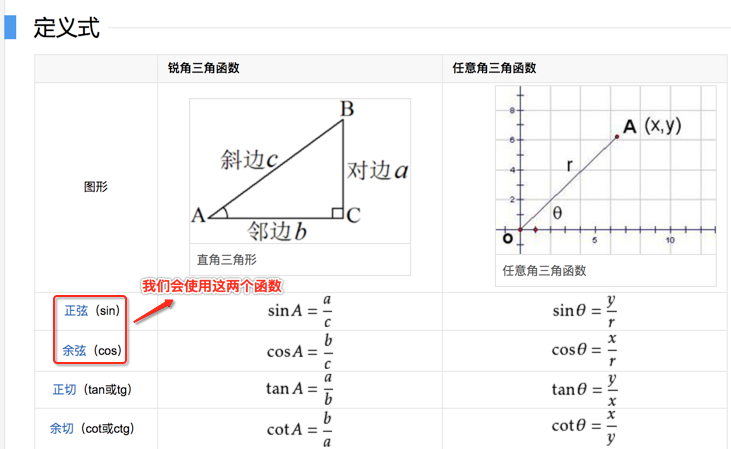
下面来看一下下图：

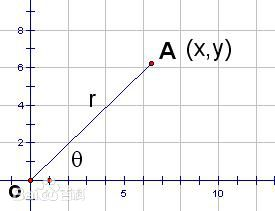
已知三角形的角度是θ，其斜边是r，那如何得到A坐标的x,y值呢？

x值:由于，所以x = cosθ * r;

y值:由于，所以y = sinθ * r;

有了上面的理论，下面通过草图来进一步分析：

①、直线的起点(与圆相交的点)的计算：

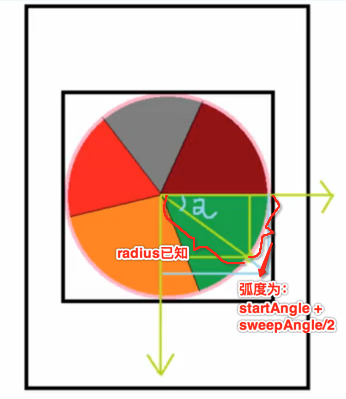
但是角度α目前是未知的，所以首要任务就是需要计算它，而目前已知弧度，很荣誉，android的Math工具类中可以根据弧度来计算，如下:

弧度α = startAngle + sweepAngle / 2;

x = radius * Math.cos(Math.toRadians(a));

y = radius * Math.sin(Math.toRadians(a));

【注】：传给Math.cos()中的参数为啥还要调用Math.toRadians(a)呢？因为这个类中参数要求的是弧度制，而不是我们数学中的角度制，所以需要用Math.toRadians转换一下。

②、直线的终点(向外延长的点)的计算：计算方法同起点，只是将原来的radius加长一点，这里我们用radius+3。

有了上面的分析，实现就比较easy了，下面开始编码：

public class PieView extends View {

    /* 数据源，由外部传过来 */
    private List<PieEntity> pieEntities;
    /* 控件的大小 */
    private int height, width;
    /* 圆的半径 */
    private int radius;
    /* 扇形组成圆形的外接短形 */
    private RectF rectF;
    /* 绘制扇形的画笔 */
    private Paint paint;
    /* 总占比 */
    private int totalValue;
    private Path path;
    /* 由于线条的颜色需要一致所以重新新建一个Paint专用于绘制直线 */
    private Paint linePaint;

    public PieView(Context context) {
        this(context, null);
    }

    public PieView(Context context, @Nullable AttributeSet attrs) {
        this(context, attrs, 0);
    }

    public PieView(Context context, @Nullable AttributeSet attrs, int defStyleAttr) {
        super(context, attrs, defStyleAttr);
        init();
    }

    private void init() {
        rectF = new RectF();

        paint = new Paint();
        paint.setAntiAlias(true);

        path = new Path();

        linePaint = new Paint();
        linePaint.setAntiAlias(true);
        linePaint.setColor(Color.BLACK);
    }

    //当自定义控件的尺寸已经决定好的时候回调
    @Override
    protected void onSizeChanged(int w, int h, int oldw, int oldh) {
        super.onSizeChanged(w, h, oldw, oldh);
        //初始化控制的宽高
        this.width = w;
        this.height = h;

        //为了防止绘制后超出屏幕区域，获取屏幕的宽高的较小值
        int min = Math.min(this.width, this.height);
        this.radius = (int) ((min * 0.7f) / 2);//圆的半径取屏幕的7成
        rectF.left = -radius;
        rectF.top = -radius;
        rectF.right = radius;
        rectF.bottom = radius;
    }

    @Override
    protected void onDraw(Canvas canvas) {
        super.onDraw(canvas);
        canvas.save();//由于用到了translate画片所以需要save一下
        //1、将画布的坐标系移到屏幕中间，这样方便去绘制圆
        canvas.translate(this.width / 2, this.height / 2);
        //2、绘制扇形
        drawPie(canvas);
        canvas.restore();
    }

    private void drawPie(Canvas canvas) {
        float startAngle = 0;
        for (int i = 0; i < pieEntities.size(); i++) {
            PieEntity pieEntity = pieEntities.get(i);
            paint.setColor(pieEntity.getColor());//设置扇形的颜色
            path.moveTo(0, 0);//需要将其移动到坐标系位置
            //其中减1是为了让各扇形区域之间有一个间隙
            float sweepAngle = (pieEntity.getValue() / totalValue) * 360 - 1;
            path.arcTo(rectF, startAngle, sweepAngle);
            canvas.drawPath(path, paint);

            //绘制每个扇形对应的直线
            double a = Math.toRadians(startAngle + sweepAngle / 2);//将角度转化为弧度
            float startX = (float) (radius * Math.cos(a));
            float startY = (float) (radius * Math.sin(a));
            float endX = (float) ((radius + 30) * Math.cos(a));
            float endY = (float) ((radius + 30) * Math.sin(a));
            canvas.drawLine(startX, startY, endX, endY, linePaint);

            //每一个扇形区域的起始点就是上一个扇形区域的终点
            startAngle += sweepAngle + 1;
            //在每次绘制扇形之后需要对path进行重置操作，这样就可以清除上一次绘制path使用的画笔的相关记录
            path.reset();
        }
    }

    /**
     * 设置饼图的源数据
     */
    public void setData(List<PieEntity> pieEntities) {
        this.pieEntities = pieEntities;
        for (PieEntity pieEntity : pieEntities) {
            this.totalValue += pieEntity.getValue();
        }
    }
}

编译运行:

文本的绘制处理

终于到最后一个步骤啦，坚持！！！先来分析一下最终效果的文本：

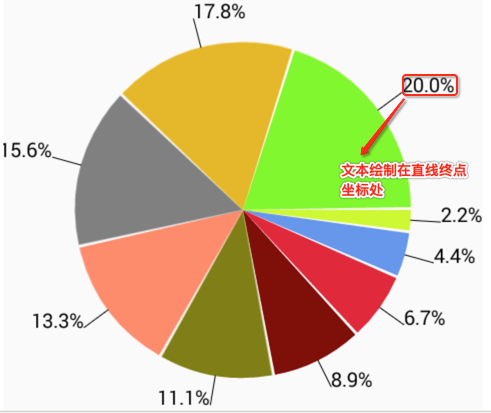
但是有个疑问？如果文本是绘制在直线的终点坐标处，按照惯例绘制都是基于左上角的点，那应该是长这样啊：

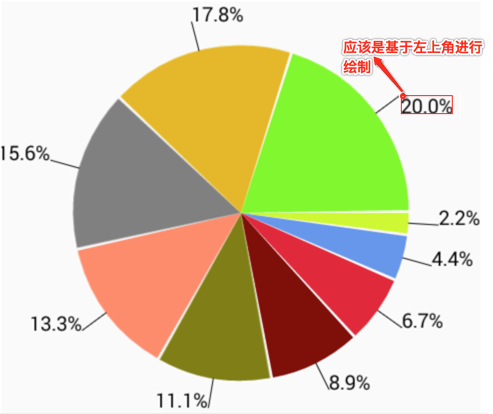
这里就有一个需要注意的点：对于文本的绘制它的基准点是左下角，而平常我们绘制其它的一些东东都是基于左上角，这个切记切记！！！

所以下面我们开始绘制文本：

编译运行:

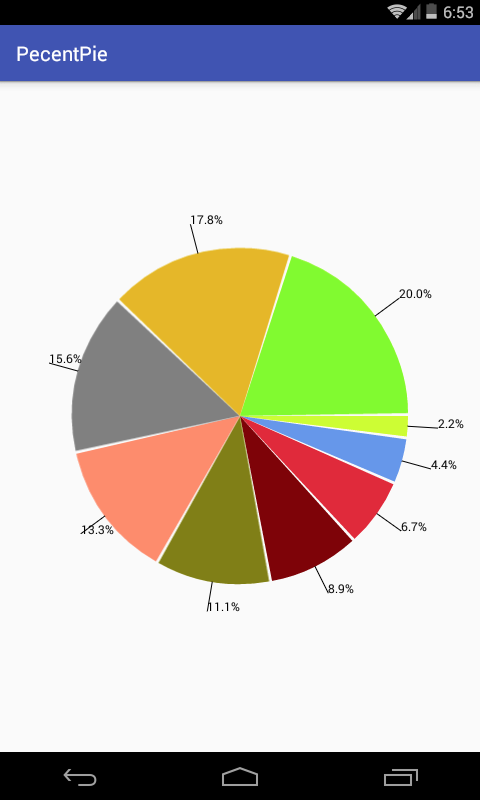
字体貌似有点小，于是乎可以加大一点：

再来看一下效果：

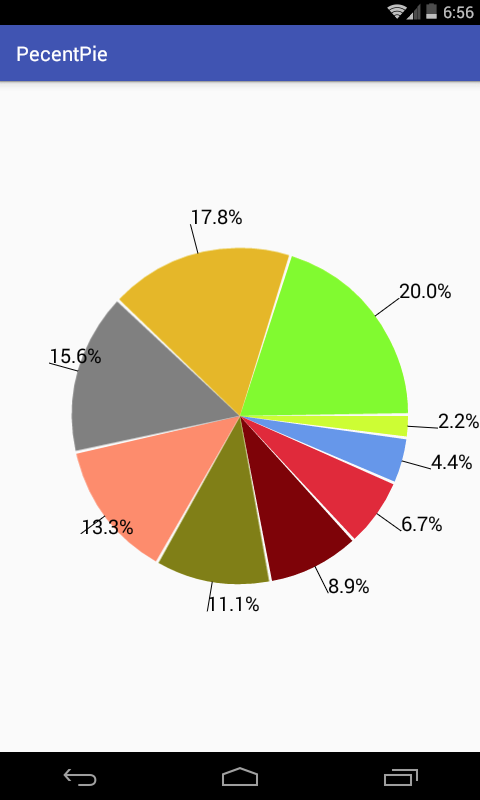
呃~~貌似圆形左边的文字有点错乱了，对比一下最终效果图：

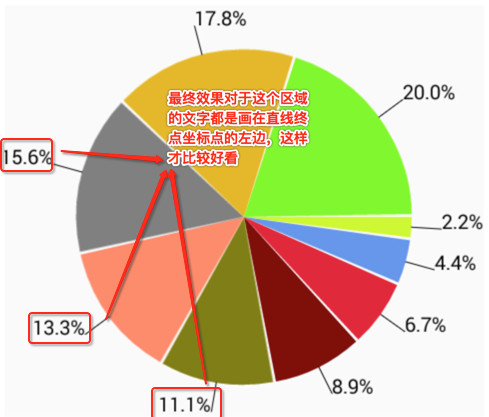
所以说需要对这种特殊区域进行一些文字处理，这里做一下规定：如果在90度~270度之间的文字让其绘制在直线左边：

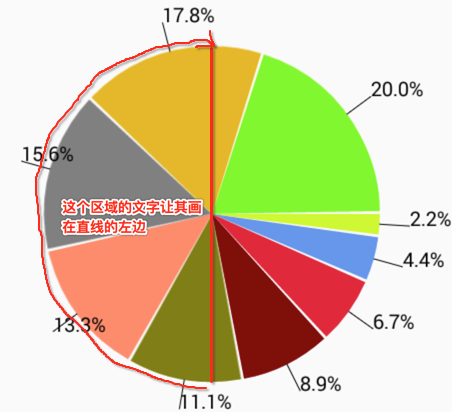
所以需要加个角度的判断对其进行一些处理：

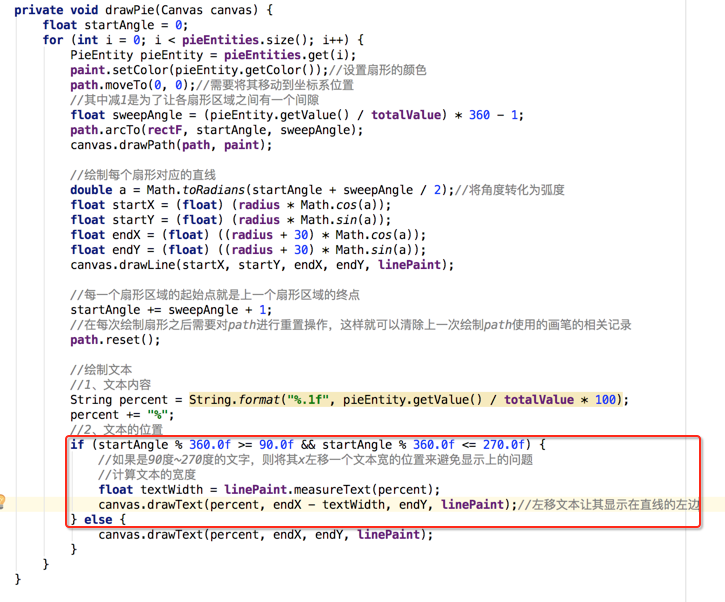
再次编译看效果：

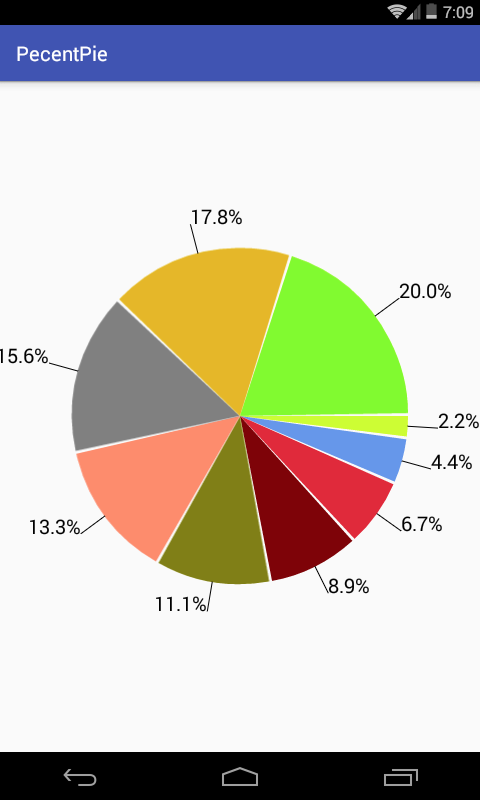
是不是就跟最终的效果差不多啦！！！不过~~对于这个文本的处理还是有些差别？

不是说文字在90度与270度之间的文本都应该是在直线的左边么，那它为啥还是在直线的右边：

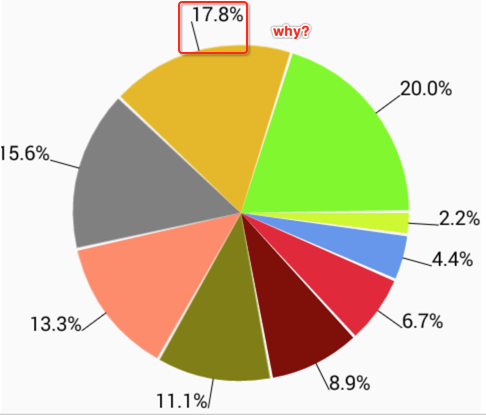
下面来打印一下日志，通过日志来解释：

编译运行，日志输出如下：

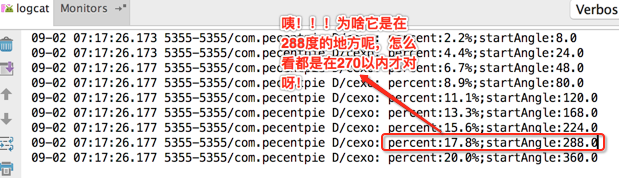
其实逻辑是没有错的，只是因为startAngle做了如下处理：

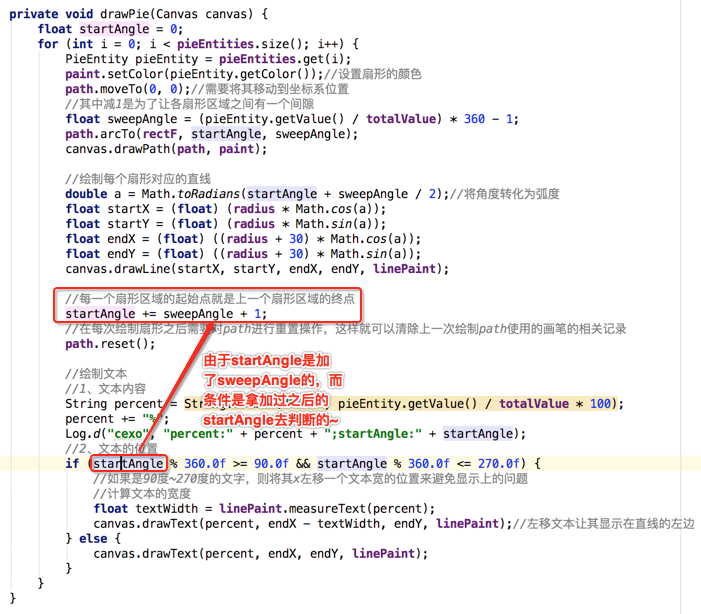
所以：

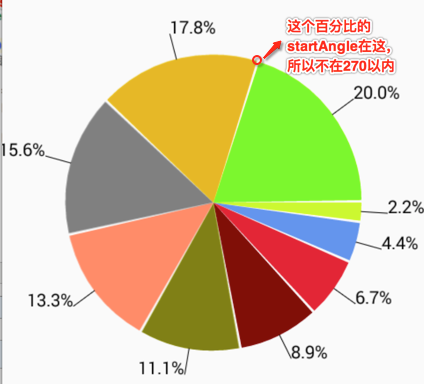
当然做得好一些的话应该是判断文字绘制的角度，也就是在startAngle基础之上减去sweepAngle/2的度数，修改代码如下：

再次运行：

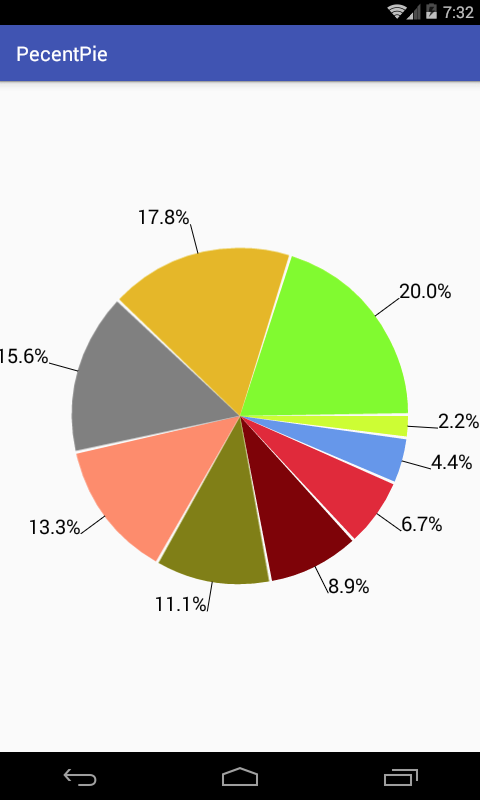
ok，完美呈现！！