BZOJ 2651 城市改建 树形DP+模拟？

题意

给一颗树，删除一条边再加一条边，使它仍为一颗树且任意两点间的距离的最大值最小。

题目数据范围描述有问题，n为1或重建不能使任意两点距离最大值变小，可以输出任意答案。

分析

删除一条边后会使它变成两颗树，两棵树的直径的中点相连一定是使距离最小的

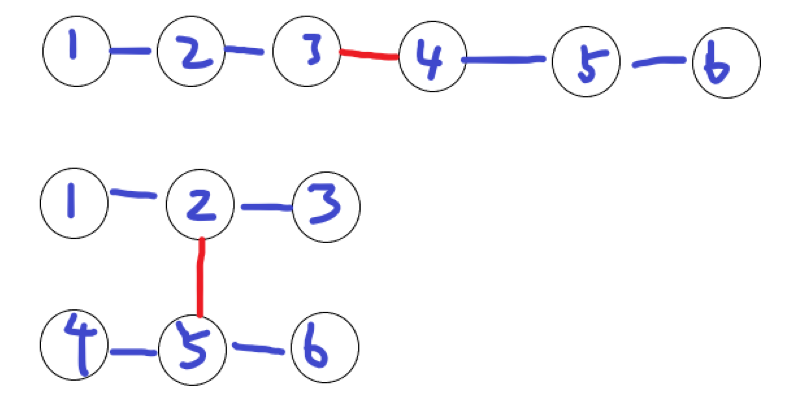
红色的边为删除重建的边

在树上dp维护每个子树的最大直径\(h[x]\)，和去除这个子树后的树的最大直径\(t[x]\)，u为x的父亲，删除u-x这条边并重建后的树的最大直径为

\[\max\{\frac{h[x]+1}{2}+\frac{t[x]+1}{2}+1,h[x],t[x]\}
\]

设\(g[u]\)为以\(u\)为根的子树中\(u\)能到达的最远距离

设\(p[u]\)为去除以\(u\)为根的子树后\(u\)能到达的最远距离

自底向上

x为u的孩子，\(mx1\),\(mx2\)分别为\(g[x]\)的最大值和次大值

• \(g[u]=max(g[x]+1)\)
• \(h[u]=max\{h[x],g[u],mx1+mx2+2\}​\)

自顶向下

k为x的兄弟，\(mx1​\),\(mx2​\)分别为\(g[k]\)的最大值和次大值

• \(p[x]=max(p[u]+1,g[k]+2)​\)
• \(t[x]=max \{p[u],h[k],p[u]+g[k]+1,mx1+mx2+2 \}​\)

然后bfs找重建的边

实现细节很多，我写的比较乱，建议自己根据dp式子模拟一下

Code

#include<bits/stdc++.h>
#define fi first
#define se second
#define bug cout<<"--------------"<<endl
using namespace std;
typedef long long ll;
const double PI=acos(-1.0);
const double eps=1e-6;
const int inf=1e9;
const ll llf=1e18;
const int mod=1e9+7;
const int maxn=3e5+10;
int n;
vector<int>f[maxn];
typedef pair<int,int> pii;
pii e[maxn];
int g[maxn],h[maxn],p[maxn],t[maxn];
int ans=inf;
pii ans1,ans2;
void dfs1(int u,int fa){
    int mx1=-inf,mx2=-inf;
    int len=f[u].size();
    int po=len;
    for(int i=0;i<len;i++){
        int x=f[u][i];
        if(x==fa){
            continue;
        }
        dfs1(x,u);
        g[u]=max(g[x]+1,g[u]);
        if(g[x]>mx1){
            mx2=mx1;
            mx1=g[x];
        }else if(g[x]>mx2){
            mx2=g[x];
        }
        h[u]=max(h[u],h[x]);
    }
    h[u]=max(h[u],g[u]);
    h[u]=max(mx1+mx2+2,h[u]);
}
int pre[maxn],suf[maxn];
int pr[maxn],sf[maxn];
void dfs2(int u,int fa){
    int len=f[u].size();
    vector<int>q;
    q.push_back(0);
    for(int i=0;i<len+5;i++) pre[i]=suf[i]=pr[i]=sf[i]=-inf;
    for(int i=0;i<len;i++){
        int x=f[u][i];
        if(x!=fa) q.push_back(x);
    }
    len=q.size()-1;
    for(int i=1;i<=len;i++){
        int x=q[i];
        t[x]=max(t[x],t[u]);
        pre[i]=max(pre[i-1],g[x]);
        pr[i]=max(pr[i-1],h[x]);
    }
    for(int i=len;i>=1;i--){
        int x=q[i];
        suf[i]=max(suf[i+1],g[x]);
        sf[i]=max(sf[i+1],h[x]);
    }
    for(int i=1;i<=len;i++){
        int x=q[i];
        p[x]=max(p[x],p[u]+1);
        t[x]=max(p[u],t[x]);
    }
    for(int i=2;i<=len;i++){
        int x=q[i];
        t[x]=max(p[u]+1+pre[i-1],t[x]);
        t[x]=max(pr[i-1],t[x]);
        p[x]=max(pre[i-1]+2,p[x]);
    }
    for(int i=1;i<len;i++){
        int x=q[i];
        t[x]=max(p[u]+1+suf[i+1],t[x]);
        t[x]=max(sf[i+1],t[x]);
        p[x]=max(suf[i+1]+2,p[x]);
    }
    for(int i=2;i<len;i++){
        int x=q[i];
        t[x]=max(t[x],pre[i-1]+suf[i+1]+2);
    }
    int mx1=-inf,mx2=-inf;
    for(int i=1;i<=len;i++){
        int x=q[i];
        t[x]=max(mx1+mx2+2,t[x]);
        if(g[x]>mx1){
            mx2=mx1;
            mx1=g[x];
        }else if(g[x]>mx2){
            mx2=g[x];
        }
    }
    mx1=mx2=-inf;
    for(int i=len;i>=1;i--){
        int x=q[i];
        t[x]=max(mx1+mx2+2,t[x]);
        if(g[x]>mx1){
            mx2=mx1;
            mx1=g[x];
        }else if(g[x]>mx2){
            mx2=g[x];
        }
    }
    for(int i=1;i<=len;i++){
        int x=q[i];
        int dis=max(max(t[x],h[x]),(t[x]+1)/2+(h[x]+1)/2+1);
        if(dis<ans){
            ans=dis;
            ans1=pii(x,u);
        }
    }
    for(int i=0;i<(int)f[u].size();i++){
        int x=f[u][i];
        if(x==fa) continue;
        dfs2(x,u);
    }
}
int pe[maxn],vis[maxn];
queue<int>q;
int bfs(int fa){
    int ret=fa;
    memset(vis,0,sizeof(vis));
    memset(pe,0,sizeof(pe));
    q.push(fa);
    vis[fa]=1;
    while(!q.empty()){
        int u=q.front();
        q.pop();
        ret=u;
        int len=f[u].size();
        for(int i=0;i<len;i++){
            if(!vis[f[u][i]]){
                q.push(f[u][i]);
                pe[f[u][i]]=u;
                vis[f[u][i]]=1;
            }
        }
    }
    return ret;
}
int fq[maxn],tot;
void dfs(int u,int s){
    if(u==0) return;
    fq[++tot]=u;
    dfs(pe[u],s);
}
int find(int x){
    tot=0;
    int s=bfs(x);
    int t=bfs(s);
    dfs(t,s);
    return fq[(tot+1)/2];
}
void work(){
    for(int i=1;i<=n;i++){
        f[i].clear();
    }
    for(int i=1;i<n;i++){
        int a=e[i].fi,b=e[i].se;
        if(a==ans1.fi&&b==ans1.se) continue;
        if(b==ans1.fi&&a==ans1.se) continue;
        f[a].push_back(b);
        f[b].push_back(a);
    }
    ans2.fi=find(ans1.fi);
    ans2.se=find(ans1.se);
    cout<<ans<<endl;
    cout<<ans1.fi<<" "<<ans1.se<<endl;
    cout<<ans2.fi<<" "<<ans2.se<<endl;
}
int main(){
    ios::sync_with_stdio(false);
    //freopen("in","r",stdin);
    cin>>n;
    for(int i=1,a,b;i<n;i++){
        cin>>a>>b;
        f[a].push_back(b);
        f[b].push_back(a);
        e[i]=pii(a,b);
    }
    dfs1(1,0);
    dfs2(1,0);
    work();
    return 0;
}