luoguP3366 【模板】最小生成树 x

P3366 【模板】最小生成树

• • 2.4K通过
  • 6.3K提交
• 题目提供者HansBug
• 标签 云端↑ 生成树
• 难度 普及-
• 时空限制 1s / 128MB

题目描述

如题，给出一个无向图，求出最小生成树，如果该图不连通，则输出orz

输入输出格式

输入格式：

第一行包含两个整数N、M，表示该图共有N个结点和M条无向边。（N<=5000，M<=200000）

接下来M行每行包含三个整数Xi、Yi、Zi，表示有一条长度为Zi的无向边连接结点Xi、Yi

输出格式：

输出包含一个数，即最小生成树的各边的长度之和；如果该图不连通则输出orz

输入输出样例

输入样例#1：

4 5
1 2 2
1 3 2
1 4 3
2 3 4
3 4 3

输出样例#1：

7

说明

时空限制：1000ms,128M

数据规模：

对于20%的数据：N<=5，M<=20

对于40%的数据：N<=50，M<=2500

对于70%的数据：N<=500，M<=10000

对于100%的数据：N<=5000，M<=200000

样例解释：

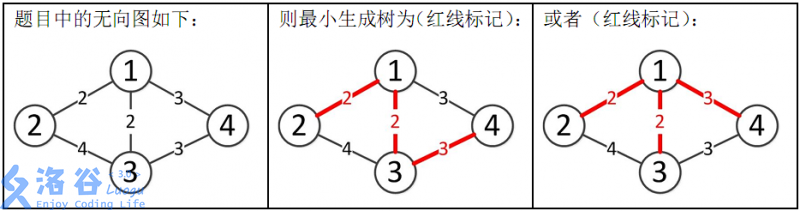
所以最小生成树的总边权为2+2+3=7

思路:

　　首先这道题是求最小生成树的模板，求最小生成树的办法有2种：

　　　　1）prim

　　　　2）kruskal

坑点:

　　1）记住要判断什么时候输出“orz”

　　2）在使用prim算法的时候，我使用的是邻接矩阵，不清楚你们用的什么，在邻接矩阵进行输入的时候，一定要进行判断一下在进行赋值！！

　　数据中有重边！！数据中有重边！！数据中有重边！！需要选取较小的一条，即算法中已经被选出来的节点不用再次进行赋值。

　　调了2天qwq，血的教训qwq（还有这种操作吗？？？orz）

上代码:

1）prim

　　在网页上找了不少题解后，突然发现，还是kruskal比较好理解。。。

　　写prim的有各式各样的2333

我就写了一种嘻嘻

#include <iostream>
#include <cstdio>
#define Maxx 0x7fffffff

using namespace std;

const int M = ;
int n,m;                                                         //n=顶点的个数，m=边的个数
int edge[M][M]={ /*输入的邻接矩阵*/ };
int lowcost[M];                                                  //记录Vnew中每个点到V中邻接点的最短边
bool visited[M];                                                 //标记某点是否加入Vnew
int pre[M];                                                      //记录V中与Vnew最邻近的点

void prim(int start)
{
     int sumweight=,i,j,k=;
     visited[start]=true;
     for(i=;i<=n;i++)
     {
         lowcost[i]=edge[start][i];
         pre[i]=start;
     }
     int minn=Maxx;                                              //最小权值
     int v=-;                                                   //所对应的下标
     for(i=;i<n;i++)                                            //进行n-1次，因为此时已经知道当前start点到另一点距离最短
     {
         minn=Maxx;
        for(j=;j<=n;j++)
        {
            if(visited[j]==false && lowcost[j]<minn)             //在Vnew之外寻找最短路径
            {
                minn=lowcost[j];                                 //最短路径
                v=j;
            }
        }
//      printf("%d %d %d\n",pre[v],v,lowcost[v]);
        if(v==-)
        {
            cout<<"orz"<<endl;
            return;
        }
        visited[v]=true;                                         //将v加Vnew中
        sumweight+=lowcost[v];                                   //计算路径长度之和
        for(j=;j<=n;j++)
        {
            if(visited[j]==false && edge[v][j]<lowcost[j])
            {
                lowcost[j]=edge[v][j];                           //此时v点加入Vnew 需要更新lowcost
                pre[j]=v;
            }
        }
    }
//  printf("the minmum weight is %d",sumweight);                 //进行输出
    printf("%d",sumweight);
}

int main()
{
    scanf("%d%d",&n,&m);
    for(int i=; i<=n; i++)
    {
//        lowcost[i]=Maxx;
        for(int j=; j<=n; j++)
            edge[i][j]=Maxx;                                     //初始化图
    }
    int x,y,w,s,Max=Maxx;
    for(int k=; k<=m; k++)
    {
        cin>>x>>y>>w;
        if(w<edge[x][y])
            edge[x][y]=edge[y][x]=w;                             //构建图
        if(w<Max)
        {
            Max=w;
            s=x;                                                 //寻找最初最"实惠"的点
        }
    }
    prim(s);                                                     //进行求解最小生成树
    return ;
}

2）kruskal

#include <algorithm>
#include <iostream>
#include <cstdio>
using namespace std;

const int N = ;
const int M = ;
int n,m,ans;
int dad[N];

struct A {
    int u,v,w;
    bool operator < (const A &qwq)const
    {
        return w < qwq.w;
    }
}t[M];

int getdad(int x)
{ return dad[x] == x ? x : dad[x] = getdad( dad[x] ); }

void kruskal()
{
    sort(t+,t++m);
    for(int i=;i<=m;i++)
    {
        int f1=getdad(t[i].u),f2=getdad(t[i].v);
        if(f1!=f2)
        {
            dad[f1]=f2;
            ans+=t[i].w;
        }
    }
    int tmp=getdad();
    for(int i=;i<=n;i++)
    {
        if(getdad(i)!=tmp)
        {
            printf("orz");
            return;
        }
    }
    printf("%d\n",ans);
}

int main()
{
    scanf("%d%d",&n,&m);
    for(int i=;i<=m;i++)
        scanf("%d%d%d",&t[i].u,&t[i].v,&t[i].w);
    for(int i=;i<=n;i++)
        dad[i]=i;
    kruskal();
    return ;
}