（题目为啥要强调用十进制输出呢,明明就是故意提醒）

分析一下样例

k=3k=3时，数列为：1,3,4,9,10,12,13..1,3,4,9,10,12,13..

转换成三进制就是：1,10,11,100,101,110,111..1,10,11,100,101,110,111..

看起来像是二进制，转化成十进制看看

1,2,3,4,5,6,7..1,2,3,4,5,6,7..

显然,第nn项就是nn.

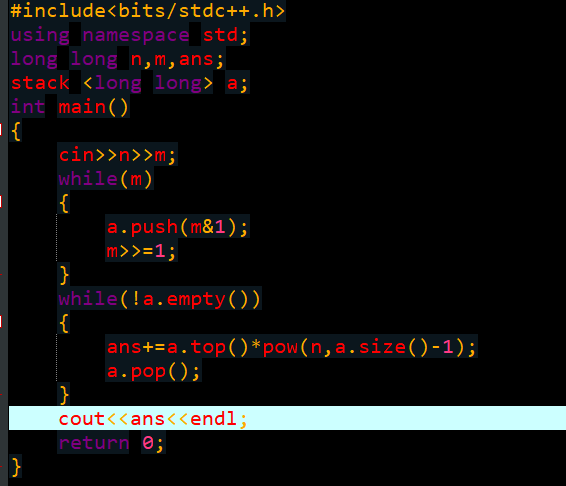
程序就把这个过程逆回去，先把nn转换成二进制，再把它当成KK进制，重新转换为十进制.

P1062 数列 题解的更多相关文章

  1. 洛谷——P1062 数列

    洛谷——P1062 数列 题目描述 给定一个正整数k(3≤k≤15),把所有k的方幂及所有有限个互不相等的k的方幂之和构成一个递增的序列,例如,当k=3时,这个序列是: 1,3,4,9,10,12,1 ...

  2. Luogu P1062 数列

    Luogu P1062 数列 题目说: 把所有$k$的方幂及所有有限个互不相等的$k$的方幂之和构成一个递增的序列. 这就是说,每一个$k$的方幂只能有或没有. 有为$0$,没有为$1$. 所以这些数 ...

  3. 洛谷P1062 数列 [2017年6月计划 数论03]

    P1062 数列 题目描述 给定一个正整数k(3≤k≤15),把所有k的方幂及所有有限个互不相等的k的方幂之和构成一个递增的序列,例如,当k=3时,这个序列是: 1,3,4,9,10,12,13,… ...

  4. Java实现洛谷 P1062 数列

    P1062 数列 import java.util.ArrayList; import java.util.Scanner; public class Main { public static voi ...

  5. [HNOI2009]有趣的数列 题解（卡特兰数）

    [HNOI2009]有趣的数列 Description 我们称一个长度为2n的数列是有趣的,当且仅当该数列满足以下三个条件: (1)它是从1到2n共2n个整数的一个排列{ai}: (2)所有的奇数项满 ...

  6. BZOJ1500：[NOI2005]维修数列——题解

    https://www.lydsy.com/JudgeOnline/problem.php?id=1500 https://www.luogu.org/problemnew/show/P2042#su ...

  7. 洛谷 P4108 / loj 2119 [HEOI2015] 公约数数列 题解【分块】

    看样子分块题应该做的还不够. 题目描述 设计一个数据结构. 给定一个正整数数列 \(a_0, a_1, \ldots , a_{n-1}\),你需要支持以下两种操作: MODIFY id x: 将 \ ...

  8. P1962 斐波那契数列-题解（矩阵乘法扩展）

    https://www.luogu.org/problemnew/show/P1962(题目传送) n的范围很大,显然用普通O(N)的递推求F(n)铁定超时了.这里介绍一种用矩阵快速幂实现的解法: 首 ...

  9. 洛谷P1062 数列

    题目描述 给定一个正整数k(3≤k≤15),把所有k的方幂及所有有限个互不相等的k的方幂之和构成一个递增的序列,例如,当k=3时,这个序列是: 1,3,4,9,10,12,13,… (该序列实际上就是 ...

随机推荐

  1. java new一个对象的过程中发生了什么

    java在new一个对象的时候,会先查看对象所属的类有没有被加载到内存,如果没有的话,就会先通过类的全限定名来加载.加载并初始化类完成后,再进行对象的创建工作. 我们先假设是第一次使用该类,这样的话n ...

  2. 数据结构实验之链表八：Farey序列（SDUT 3331）

    #include <bits/stdc++.h> using namespace std; typedef struct node { int data2; int data1;//mu ...

  3. python2.X与Python3.X区别

    __future__模块 [回到目录] Python 3.x引入了一些与Python 2不兼容的关键字和特性,在Python 2中,可以通过内置的__future__模块导入这些新内容.如果你希望在P ...

  4. codeforces#1157D. Ehab and the Expected XOR Problem（构造）

    题目链接: http://codeforces.com/contest/1174/problem/D 题意: 构造一个序列,满足以下条件 他的所有子段的异或值不等于$x$ $1 \le a_i< ...

  5. POJ 1741 Tree ——（树分治）

    思路参考于:http://blog.csdn.net/yang_7_46/article/details/9966455,不再赘述. 复杂度:找树的重心然后分治复杂度为logn,每次对距离数组dep排 ...

  6. 解惑spring事务传播特性之嵌套事务

    /** * Support a current transaction, create a new one if none exists. * Analogous to EJB transaction ...

  7. windows下手动安装composer

    原文地址:http://www.cnblogs.com/JANCHAN/p/7735882.html 1.下载compser.phar 地址 https://getcomposer.org/downl ...

  8. ElasticSearch2:集群安装

    0.Linux系统参数设置 Linux进程数系统限制查看 [root@ip101 config]# sysctl kernel.pid_max kernel.pid_max = 131072 [roo ...

  9. 异常值检验实战1--风控贷款年龄变量(附python代码)

    python风控评分卡建模和风控常识(博客主亲自录制视频教程) https://study.163.com/course/introduction.htm?courseId=1005214003&am ...

  10. nginx详解（代理服务器的解释+nginx 在linux 下的安装+nginx.conf 中的配置解释）

    一.概论 1.什么是代理服务器 代理服务器,客户机在发送请求时,不会直接发送给目的主机,而是先发送给代理服务器,代理服务接受客户机请求之后,再向主机发出,并接收目的主机返回的数据,存放在代理服务器的硬 ...