Spectral Norm Regularization for Improving the Generalizability of Deep Learning论文笔记

Spectral Norm Regularization for Improving the Generalizability of Deep Learning论文笔记

2018年12月03日 00:03:07 RRZS 阅读数 153更多

分类专栏： 深度学习 cv

 

版权声明：本文为博主原创文章，遵循CC 4.0 BY-SA版权协议，转载请附上原文出处链接和本声明。

本文链接：https://blog.csdn.net/beyondjv610/article/details/84722476

这篇文章的贡献点在于提出了一种新的正则化方法，并证明了其相比于其他的正则化方法具有更好的效果（测试集误差更低以及训练误差和测试误差之间的gap更小），之后的gan网络很多都沿用了这个正则化的方法，也验证了该方法的有效性。

一、Spectral Norm Regularization

1.1谱范数的提出

首先，作者提出了衡量扰动的计算公式：

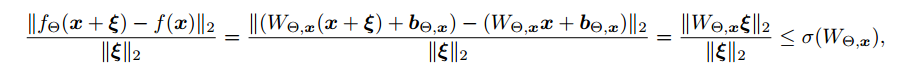
该公式衡量当x发生一定程度变化时，y变化的大小。根据上述公式我们定义了谱范数，对于一个矩阵A

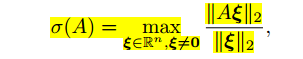
根据数学推导可以得出，A的谱范数等于其最大的特征值【1】。我们希望Y函数尽可能的平滑就需要约束A的谱范数尽可能地小。

在神经网络中，上述A就是对应Y = WX+b中的W，其中这个W是指x到最终输出的映射，而不是某一层的W。所以，我们可以将其化为每一层的激活函数DL与对应的WL相乘得：

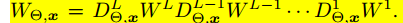
一方面，两个矩阵相乘的谱范数不大于两个矩阵对应的谱范数相乘；另一方面，如果我们使用常见的分段激活函数，比如relu，当x大于等于0时，DL取值为1，否则，DL取值为0，所以其对应的谱范数必然小于等于1，所以有如下的推导（当然如果我们使用sigmoid之类的函数，我们需要对不等式的右边乘上一个常数）：

所以，如果我们需要约束整个神经网咯的谱范数，只需要对每一层的谱范数进行约束即可。

1.2谱范数的计算：

前面部分我们提到了矩阵A的谱范数等于其最大的特征值，这里贴出其证明过程【1】：

论文中使用的是（15），但是本文的证明用的是（13）和（14）。

下面给出迭代有效性的证明：

因此，我们通过u，A，v就可以得到最大特征值，从而得到A的谱范数。

在Keras中，可以通过下述代码计算谱范数

1.  
   def spectral_norm(w, r=5):
2.  
   w_shape = K.int_shape(w)
3.  
   in_dim = np.prod(w_shape[:-1]).astype(int)
4.  
   out_dim = w_shape[-1]
5.  
   w = K.reshape(w, (in_dim, out_dim))
6.  
   u = K.ones((1, in_dim))
7.  
   for i in range(r):
8.  
   v = K.l2_normalize(K.dot(u, w))
9.  
   u = K.l2_normalize(K.dot(v, K.transpose(w)))
10.  
    return K.sum(K.dot(K.dot(u, w), K.transpose(v)))

二、各种正则化方法

1.Weight decay

作者认为这种训练方法对整个W矩阵进行约束，可以理解为对其所有方向的特征向量进行约束，会影响模型的表达能力，从而影响预测的结果，而作者的方法只是对最大的特征值进行约束，对于其他跟该特征向量垂直的特征向量则不会有影响，从而对模型表达能力的影响较小。

2.Adversarial training

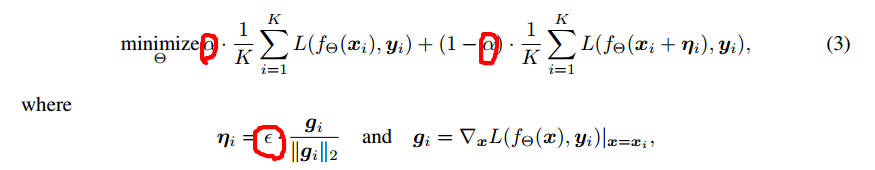
其中圈圈是超参数，第一个代表对于对抗样本关注的程度，取值为（0,1），第二个表示控制对抗样本与真实样本在梯度方向上的距离，其值越大，对模型的泛化能力要求越高。从上述公式可以看出，该优化函数要求模型不仅仅在真实样本上的误差尽可能小，同时要求在对抗样本（真实样本加上损失函数在真实样本上的梯度得到对抗样本）上的误差尽可能小，从而可以让损失函数在真实样本点附近的曲线尽可能平滑，减少误差。作者认为其只关注训练样本点附近的损失函数尽可能平滑，而无法考虑到测试样本附近损失函数尽可能平滑。

3.Jacobian regularization

约束y对x的梯度，由于计算的复杂度过高，可以简化为每一层输出对该层输入梯度的惩罚：

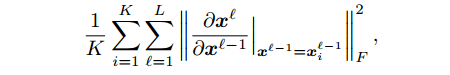
这种方法本质上和第一种方法一样，如果我们忽略激活函数影响的话。

三、实验结果分析

3.1评价指标

（1）测试集上面的预测准确率

（2）训练集和测试集之间的Generalization Gap，作者做了如下的定义。

对于某个参数a，其对应的Generalization Gap在所有测试集的准确率高于a的情况中，选择训练集和测试集之间的最小的差值作为Generalization Gap。具体可以在模型训练过程中，不断地保存训练集的准确率和测试集的预测准确率，然后选取测试集的结果大于a的checkpoint去计算训练和测试误差的gap，并选取最小值。

3.2结果分析

从上图可以看出，decay 和spectral无论在测试误差都优于其他两种方法，同时spectral在batch变大的情况下，其精度损失比其他的三种方法小。对于generalization gap，spectral仍然取得最好的效果。

3.3

从图2a可以看出，gap与训练数据的L2梯度的norm成反比，说明我们约束训练时候的L2norm是没有意义的，而从图2b可以看出，gap与测试数据的L2梯度的norm成正比，所以我们降低测试时候的L2norm可以降低gap。但是，我们无法得知测试集的数据，自然无法得知他的L2norm，而我们spectral norm则约束任意点的L2norm，则可以很好解决这个问题。

下面，我们回归到我们模型的本质，即为了使模型在测试集上误差尽可能的小，这个可以转化为两个问题：（1）在训练集上面误差尽可能小；（2）训练误差和测试误差之间的gap尽可能小。我们的spectral norm刚好可以很好的解决这个问题。不像decay的方法对整个W进行约束，从而约束了模型的表达能力，从而导致训练误差的增加。同时，spectral norm的引入可以降低gap，从而使得测试的效果相比其他的方法更好。

3.3

3.4W矩阵的奇异值

从图4可以看出，spectral norm的奇异值会低于其他的方法，而低的奇异值也对应于小的gap，从而从侧面验证了spectral norm可以降低gap。

相关知识：

N. S. Keskar, D. Mudigere, J. Nocedal, M. Smelyanskiy, and P. T. P. Tang. On large-batch training for
deep learning - generalization gap and sharp minima. In ICLR, 2017.

参考文献：

【1】苏剑林. (2018, Oct 07). 《深度学习中的Lipschitz约束：泛化与生成模型 》[Blog post]. Retrieved from https://kexue.fm/archives/6051

疑惑：

为什么大的batch size会导致泛化能力下降。参见相关知识。