数据结构3——浅谈zkw线段树

MENU

1、建树（普通）

2、普通操作*4

3、差分思想*5

本文作者frankchenfu，blogs网址http://www.cnblogs.com/frankchenfu/，转载请保留此文字。

　线段树是所有数据结构中，最常用的之一。线段树的功能多样，既可以代替树状数组完成“区间和”查询，也可以完成一些所谓“动态RMQ”（可修改的区间最值问题）的操作。其中，它们大部分都是由递归实现的，因此就有一些问题——栈空间占用大和常数大。

　　因此，从中便衍生了一种非递归式的线段树（作者是THU的张昆玮，参见他自己的PPT讲稿《统计的力量-线段树》），命名为zkw线段树。

　　以下内容均用zkw线段树保存区间最大值作为演示。如果代码细节上有问题，请大家以自己写的为准，也欢迎向我反馈。

1、建树

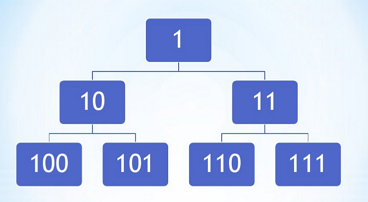
　　我们可以先观察左边面这张图。这张图本来是一张堆式的树形图，这里把它转化成了二进制。从中，我们可以发现最底层的节点舍去最低位，也就是说向右移一位之后，就变成了他们的父节点。同理，第二层中的结点也可以通过相同的方式变成根节点。

　　因此，我们在构建这棵树时，就可以利用计算机的二进制建树，达到快速简单的目的。

　

　

　　zkw线段树的操作几乎没有出现递归，而是用循环代替。例如建树操作（d数组存储数值）：

void build(int n)
{
    for(bit=;bit<=n+;bit<<=);
    for(int i=bit+;i<=bit+n;i++)
        scanf("%d",&d[i]);
    for(int i=bit-;i;i--)
        d[i]=max(d[i<<],d[i<<|]);
        //i<<1|1 = (i<<1)+1 = 2*i+1
}   

（这里解释一下，bit表示非叶子节点，即倒二层及以上的节点数，每个节点保存的是它的值，如：和，最大值，最小值……）

　　而普通的线段树建树则类似于（代码来自这里）：

struct SegTreeNode
{
    int val;
}segTree[MAXNUM];//定义线段树

void build(int root, int arr[], int istart, int iend)
{
    if(istart == iend)//叶子节点
        segTree[root].val = arr[istart];
    else
    {
        int mid = (istart + iend) / ;
        build(root*+, arr, istart, mid);//递归构造左子树
        build(root*+, arr, mid+, iend);//递归构造右子树
        //根据左右子树根节点的值，更新当前根节点的值
        segTree[root].val = min(segTree[root*+].val, segTree[root*+].val);
    }
}

　　很简单的例子，说明了zkw线段树不仅不需要递归，而且在代码上也更简洁。

2、普通操作

　　既然是线段树，那么就肯定能完成修改与查询操作。

2.1 单点修改——二进制思想的运用

　　单点修改也不难，他的思想就是先把叶节点修改，然后依次维护父节点（把所有和它有关的的修改掉）。例如这样：

void update(int x,int y)
{
    for(d[x+=bit]=y,x>>=;x;x>>=)
        d[x]=max(d[x<<],d[x<<|]);
}

　　这个代码就更为简短了（这里就不拿出来对比了）。

　　当然，如果不是整个修改，而是加上或减去某数，只需要将for循环中的 d[x+=bit]=y 改为 d[x+=bit]+=y 即可（这里统一用整体修改作示范，下同）。

2.2 单点查询——最简单的查询

　　假设数组中有 x 个元素，二叉树层数为 m，那么这 x 个元素在这个满二叉树中的编号就是$2^m$和$2^m+x-1$之间，即第x个元素就是$2^m+x-1$，访问起来很方便。

2.3 区间查询——单点查询的升级版

　　区间查询也不难，规律同上，就是沿区间往上找。这里就直接上代码。

int query(int s,int t)
{
    int ans=-;
    for(s+=bit-,t+=bit+;s^t^;s>>=,t>>=)
    {
        if(~s&)
            ans=max(ans,d[s^]);
        if(t&)
            ans=max(ans,d[t^]);
    }
    return ans;
}

2.4 区间修改——差分思想

　　区间修改这时候看起来就很难办了……呃，怎么办呢？？

　　经过作者一个中午的实验，发现，用上述代码的思想似乎较难完成O($log_2$ n)级别的区间修改。这时候，翻开zkw神犇PPT讲稿，发现……原来，可以用差分的思想。（事实上，在普通线段树中，可以使用“懒标记”思想，不过限于作者水平，这里不再展开讨论）

3、差分思想

差分？

　　差分是化绝对为相对的重要手段。我们接下来，数组里的d值就不在存最大值$d_n$了，而是另外开个数组m，存$m_n = d_n - d_{\frac{n}{2}} $，让每一个结点的值都是存他与他父亲结点的差值。

有什么用吗？

　　当然有（不然说了干什么）！这时候，我们进行区间修改，就只需要修改$m_n$的值。

　　这时候查询可以完成吗？可以。

　　单点查询就是在m数组中，从要查的结点一直查到根结点，再加上d数组的值，就可以找到答案（这个应该很好理解吧）。

小插曲

　　然后，我们在写代码的时候会发现，如果我们把d数组初始化为0的话，那么所有的修改都记在数组m中，d数组的值会变吗？不会。

　　因此，我们干脆连值也不存了，把差分的“标记”直接当作值。于是，基本的差分思想就出来了。

　　不过，值得一提的是，在常数上，差分的写法可能更大一些（不一定会明显优于递归版的普通线段树）。

3.1 差分思想与建树

这时候，每个点就像前面说的，存差就好了。代码如下，应该很好理解：

void build(int n)
{
    for(bit=;bit<=n+;bit<<=);
    for(int i=bit+;i<=bit+n;i++)
        scanf("%d",&d[i]);
    for(int i=bit-;i;i--)
    {
        d[i]=min(d[i<<],d[i<<|]);
        d[i<<]-=d[i];d[i<<|]-=d[i];
    }
}

3.2 差分思想与单点修改

　　你当然可以尝试区间修改，然后用像 query(,,x) 这样的方法修改。

不过完全没有这个必要。

void update(int s,int t,int x)
{
    int tmp;
    for(d[s]+=x;s>;s>>=)
    {
        tmp=max(d[s],d[s^]);d[s]-=tmp;d[s^]-=tmp;d[s>>]+=tmp;
        s>>=;
    }
}

3.3差分思想与单点查询

　　不得不承认，差分思想的运用，唯一一个不好的地方就是单点查询从O(1)变为了O($log_2$ n)，但是他可以帮助我们完成区间修改的操作，因此也只好忍受一下了。

因为差分存储方式的运用，相应的，这时候的代码就成了这样：

void query(int x)
{
    int res=;
    while(x)
        res+=d[x],x>>=;
    return res;
} 

3.4差分思想与区间修改

就为了这个区间查询，我们几乎把内容翻了一倍——讲差分存储方式。而这种方式就是能够让我们完成区间修改。修改方式在上面介绍差分作用时提过了，这里就不在赘述了。代码：

void update(int s,int t,int val)
{
    s+=bit;t+=bit;int tmp;
    if(s==t)
    {
        for(d[s]+=val;s>;s>>=)
        {
            tmp=min(d[s],d[s^]);d[s]-=tmp;d[s^]-=tmp;d[s>>]+=tmp;
        }
        return;
    }
    for(d[s]+=val,d[t]+=val;s^t^;s>>=,t>>=)
    {
        if(~s&)d[s^]+ =val;
        if(t&) d[t^]+=val;
        tmp=min(d[s],d[s^]);d[s]-=tmp;d[s^]-=tmp;
        d[s>>]+=tmp;tmp=min(d[t],d[t^]);
        d[t]-=tmp;d[t^]-=tmp;d[t>>]+=tmp;
    }
    for(;s>;s>>=)
    {
        tmp=min(d[s],d[s^]);d[s]-=tmp;d[s^]-=tmp;
　　　　 d[s>>]+=tmp;
    }
    return;
}

3.5差分思想与区间查询

区间查询？其实和之前没用差分的差不多，只是把它求出来之后，再把值依层还原回去。

int query(int s,int t)
{
    int lans=,rans=,ans;
    if(s==t)
    {
        for(s+=bit;s;s>>=)
            lans+=d[s];
        return lans;
    }
    for(s+=bit,t+=bit;s^t^;s>>=,t>>=)
    {
        lans+=d[s];rans+=d[t];
        if(~s&) lans=min(lans,d[s^]);
        if(t&) rans=min(rans,d[t^]);
    }
    lans+=d[s];rans+=d[t];
    for(ans=min(lans,rans);s>;)
        ans+=d[s>>=1];
    return ans;
}

至此，zkw线段树的基本操作到这里就讲完了。让我们回顾一下，zkw线段树的优点不仅在于常数小，空间小（对于一般情况下的写法），而且好写好调，是一种优秀的数据结构。它的本质是非递归式线段树。希望这篇博客的内容对大家有帮助，满意请在右下方点个赞，谢谢。