Machine Learning

Classification

使用线性回归来分类，会很不准确。并且，它的范围也会超出 {0, 1}。所以使用下面的逻辑回归模型。

Hypothesis representation

线性回归中 h_θ(x) = θ^Tx，而在逻辑回归中，我们想要 h_θ(x) ∈ [0, 1]。对结果进行双曲化处理：

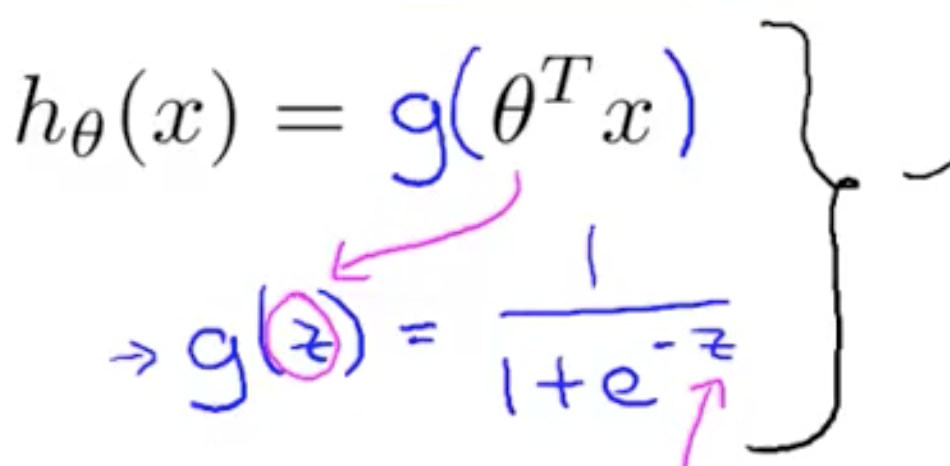
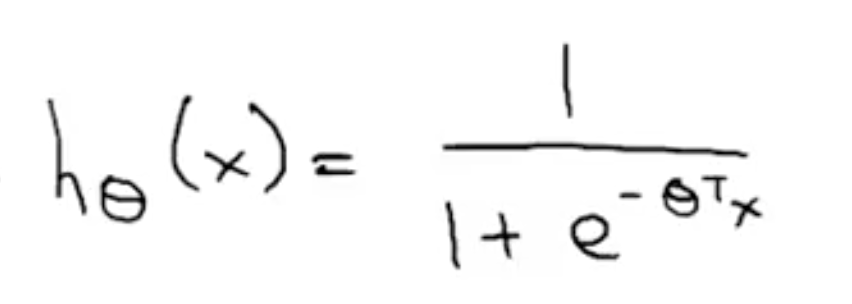
，图象如右图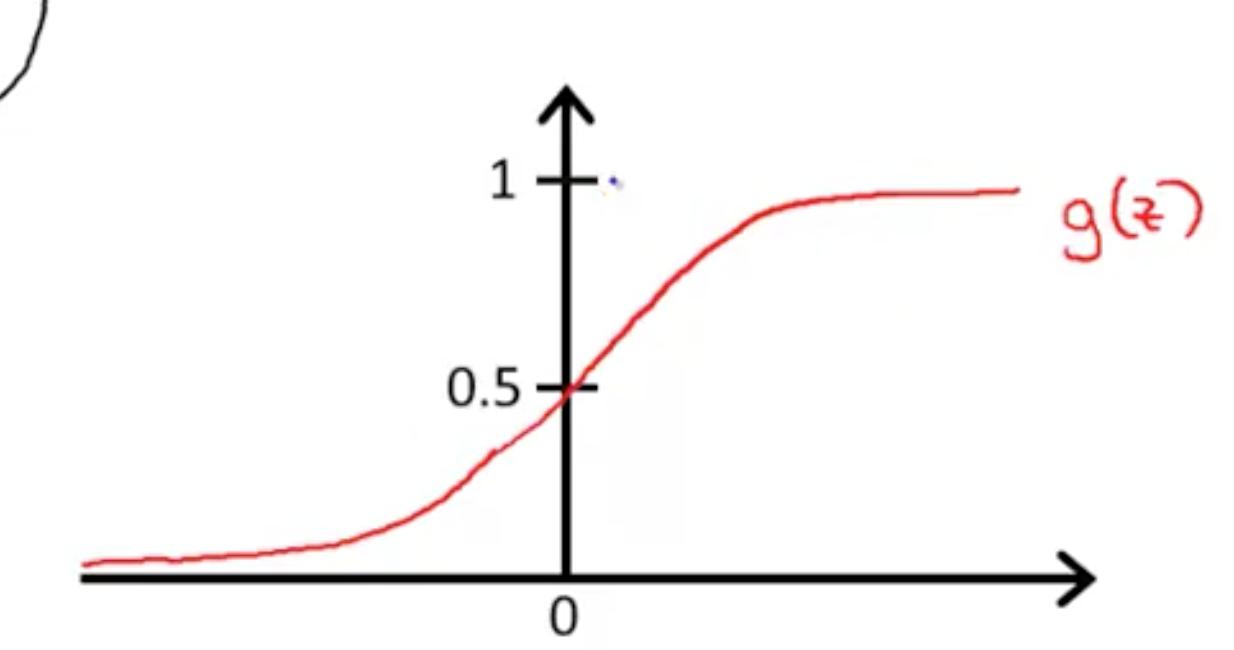：，范围是 (0, 1)。

在线性回归中，h_θ(x) 就表示 y 的值。在逻辑回归中，表示『基于输入的 x，y=1 的概率是多少』。用数学形式表示：。

Desicion boundary

逻辑回归中， h_θ(x) 是属于 (0, 1) 范围内的连续的值。但我们的分类结果只有 0 或者 1，所以就需要一个决策边界。这里，取平均值， y = 0.5。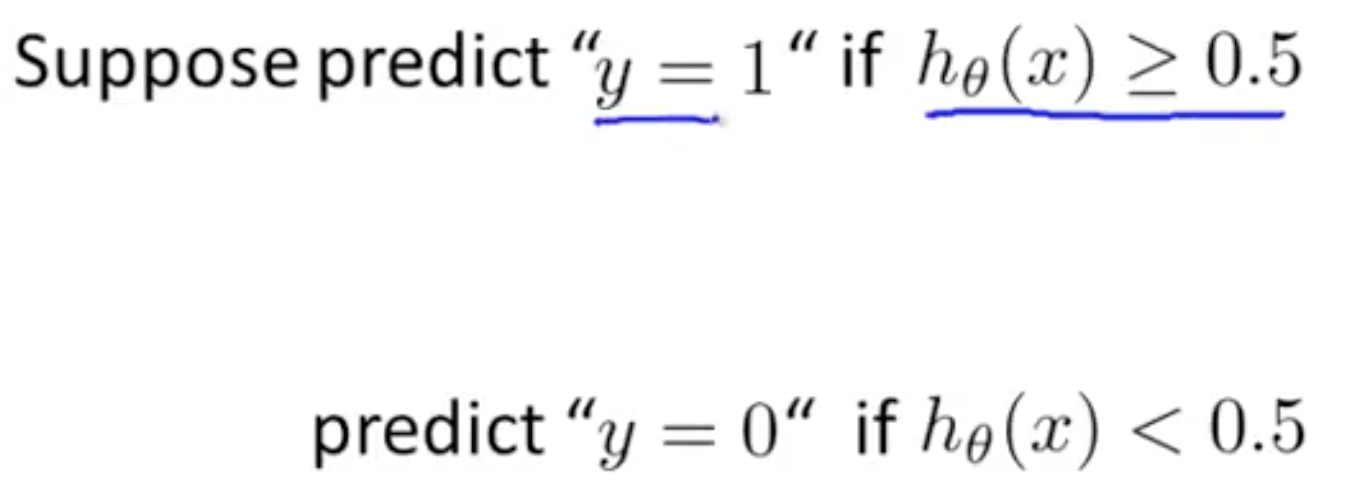。从上方的双曲线图中可以看出，当 z > 0，y=1，即 θ^Tx >= 0 时，h_θ(x) >= 0.5。将区域分为 y=0 和 y=1 的两个区域。

决策边界是针对与 θ 的属性，所以 θ 不同，决策边界也不同。

非线性的决策边界

当 h_θ(x) 是多项式的时候，。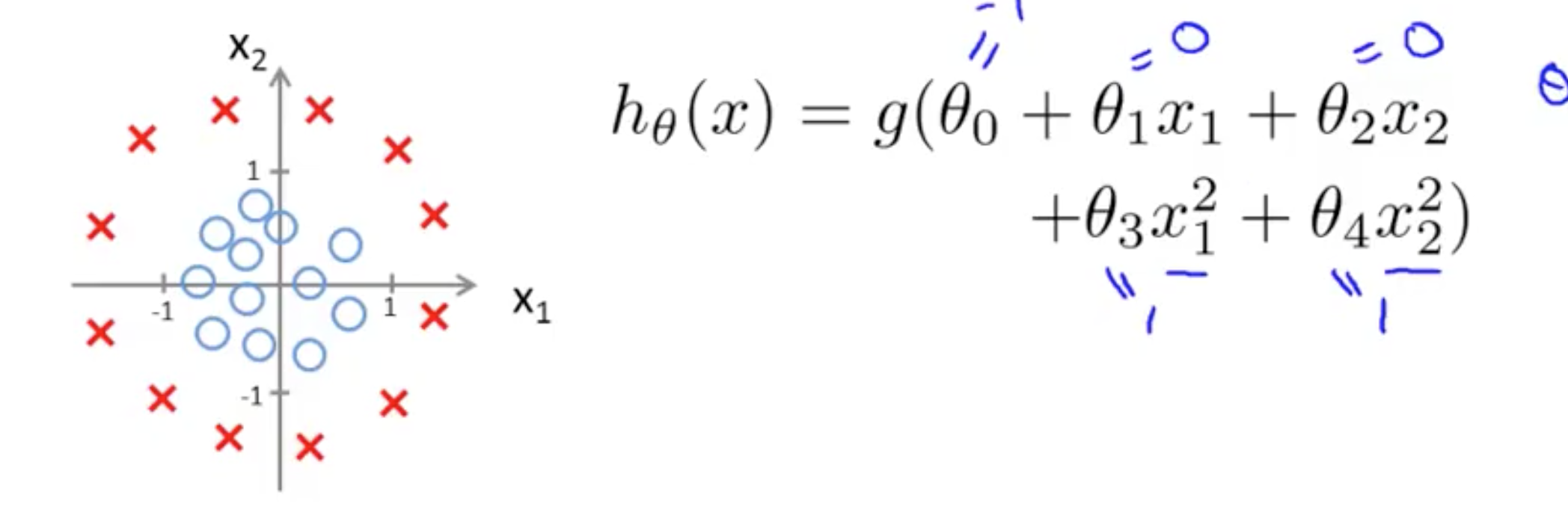

当多项式更加复杂的时候，决策边界的形状也会更加复杂。

Cost Function

当 y = 1 时，如果 hθ(x) = 0，那么 cost 接近无限大。因为你预测不是恶性肿瘤，但实际上是恶性肿瘤。同样，如果不是恶性肿瘤，你预测 y = 1 的概率越接近 1，那么误差越小。

y = 0 时的情况同理可得。

化简的 Cost Function 和 Gradient Descent

化简后（通过遍历所有情况能够证明）

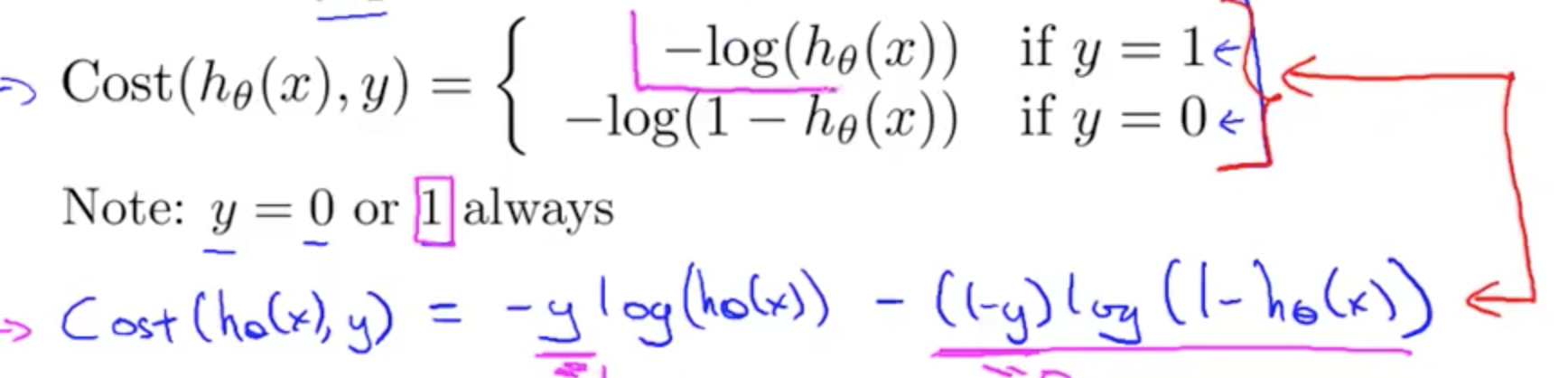
J(θ) 为

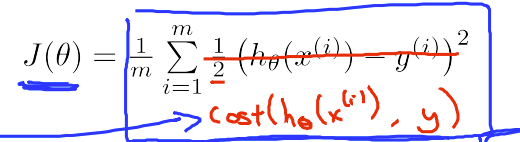
Gradient Descent

Logistic Regression 与 Linear Regression 在 Gradient Descent 上的不同，就是 hθ(x) 的不同。

用矩阵计算为：

grad = (X' * (h - y)) / m;

　这里是求和，所以最终是 1*1，所以转置成这样的形式 [1 * n] * [n * 1]。

Advanced Optimization

使用更高级的算法，不需要手动选择 learning rate；通常比 gradient descent 更快；缺点是更复杂。

可以使用库直接调用这些算法，不需要深入理解它们。

% 我们传入了 GradObj，最大循环次数为 100 次

octave:1> options = optimset('GradObj', 'on', 'MaxIter', '100')

options =

  scalar structure containing the fields:

    GradObj = on

    MaxIter = 100

octave:2> initialTheta = zeros(2,1 )

initialTheta =

   0

   0

jVal 表示 j(θ) 的计算方法

gradient 表示对应 θ 的计算方法（求导）

Multiclass Classfication

大于 2 个类别，如邮件分类：工作、朋友、家庭。

使用 one-vs-rest 方法。

假设有 3 类，我们将测试数据分为 C₃²类别，把一类看作 positive，其他类看做 negative。这样我们就能得到三个 h(θ)

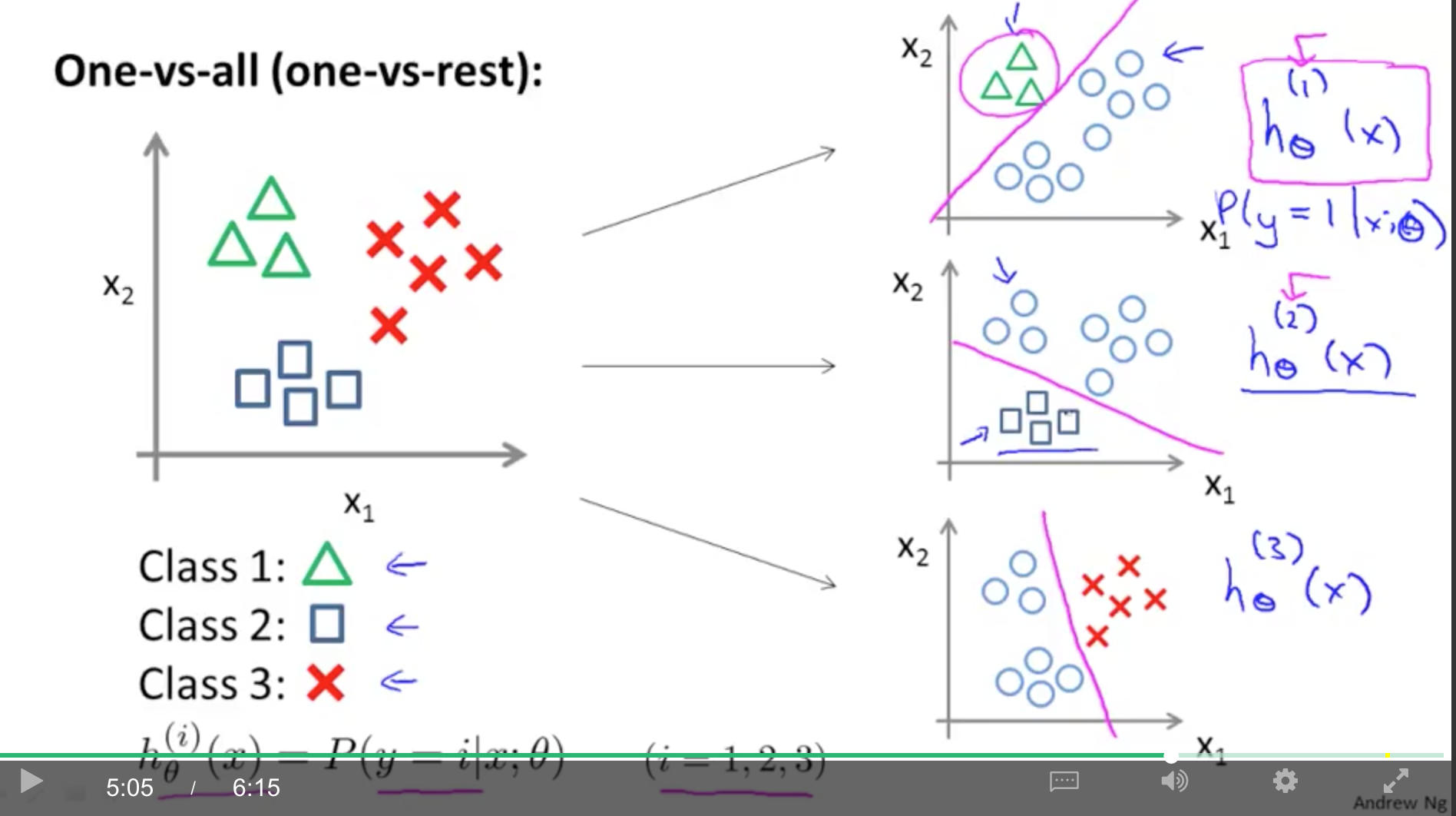
在预测时，由于有三个 h(θ) 函数，所以有三个结果。一般是取概率最大的作为最终预测结果。

习题

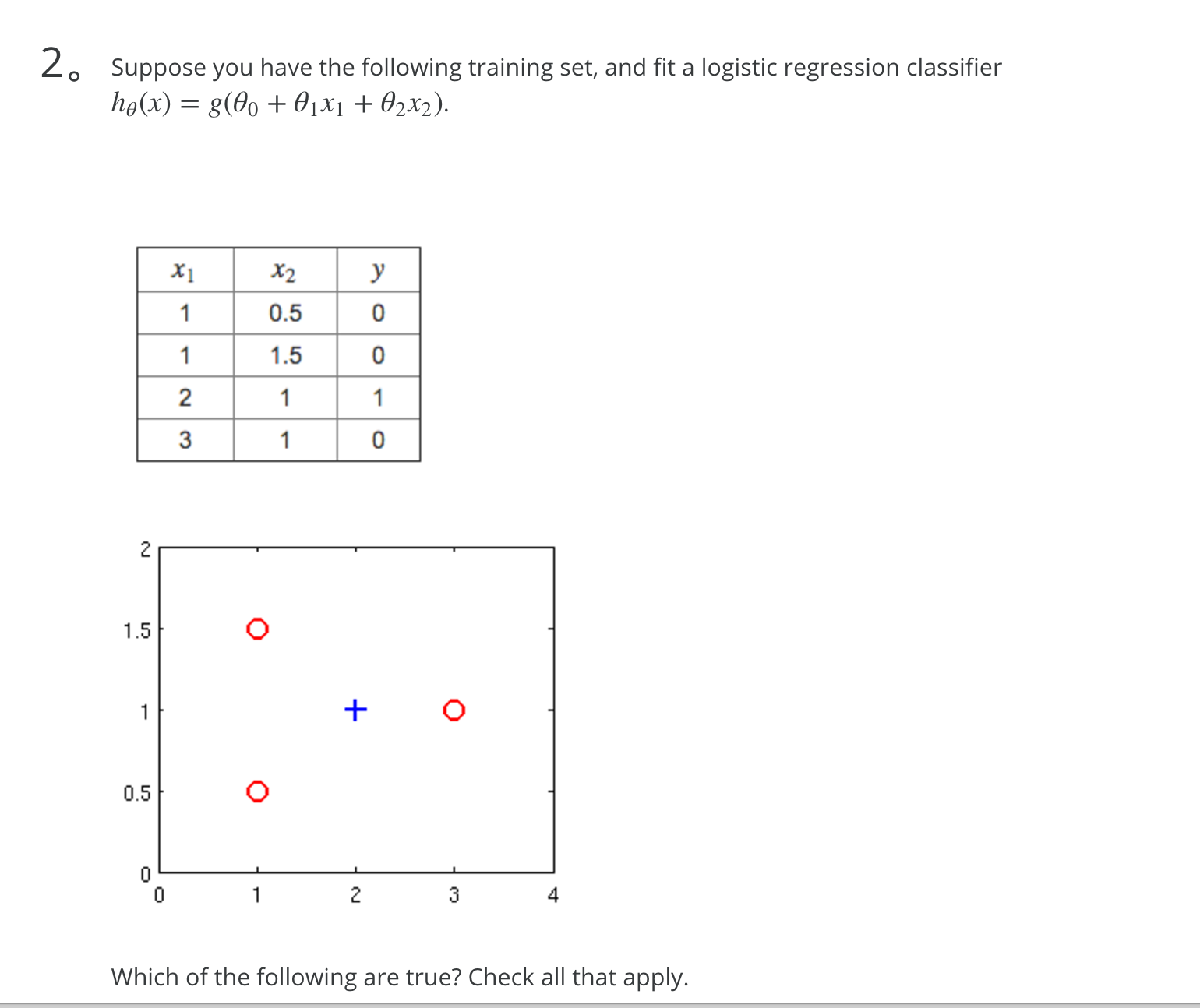
从图中可以可以看出，应该是一个圆把蓝色的圈住，所以应该有两个 x²

1. 如何判断是否 convex，gradient 什么情况下(能/否) converge

- 判断 convex 要由数学证明完成，我们是选择别人证明好的 cost function，这里不做证明。

- 确保 learning rate α 被设置合适。

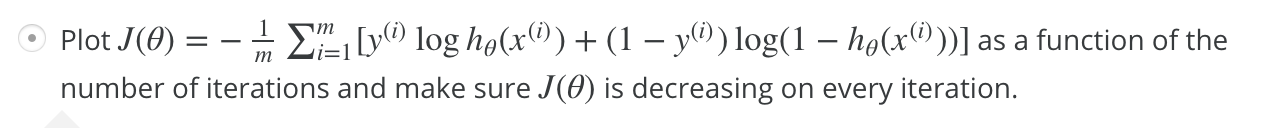
2. 增加多项式 features 可以增加对训练数据的匹配。更匹配的意思是：使曲线与数据更贴近。

对。

3. 能否被直线分割为两段有什么区别？对 converge 有影响吗？

不知道。应该没有

non-linear decision boundaries

4. linear regression 与 logistic regeress 的区别？两者会相同吗？在什么情况下会相同？

Gradient Descent 的公式是一样的，但是 h_θ(x) 不一样

为什么 h_θ(x) 要不一样呢？

想要 0 < hθ(x) < 1，所以定义了 Logistic function (sigmoid function)。

还是有错误。

有错误

第二个选项：应该对的。J(θ) 表示的是误差。

第三个选项：没有理解清楚。算错误的

第四个选项：

没有提到 local minimum，但我认为有这个原因。

如何用 vector 表示 J(θ)

从课件中查到公式为，所以 3、4 是对的。

1 是错误的。

θ^Tx - y⁽ⁱ⁾为 n * 1 的 vector。乘以 x 第 i 行。应该是乘以 x 第 i 行第 j 个，其中 j 是不变的。所以是错误。

第一个，对的

第二个，意思是：允许你对于每个 y 来自固定的、离散的几组值。对的。

第三个，对。范围就是 >= 0 不会变

第四个，对

存在错误。