最小割树(Gomory-Hu Tree)

前置知识

Gomory-Hu Tree是用来解决无向图最小割的问题的，所以我们需要了解无向图最小割的定义

和有向图类似，无向图上两点(x,y)的割定义为一个边集E，满足去掉该边集后x,y不联通。最小割即为所有的割中权值之和最小的割

通过这条割我们把点集划为两个部分，x所在的一个记为\(V_x\),y所在的一个记为\(V_y\)

定义

首先我们知道，一个n个点的无向图上，两点之间本质不同的最小割只有n-1种，因此一定存在一棵树，满足树上两点的最小割等于原图上两点的最小割。

最小割树的定义如下：

定义一棵树T为最小割树，如果对于树上的所有边(s,t)，树上去掉(s,t)后产生的两个集合恰好是原图上(s,t)的最小割把原图分成的两个集合，且边(u,v)的权值等于原图上(u,v)的最小割

很多博客里把Gomory-Hu树定义为树上边(u,v)的权值=图上(u,v)的最小割，而忽视了删掉边(u,v)后点集的关系，是错误的。那是等价流树(Equivalent Flow Tree)的定义。如果最小割树不是像上面一样定义的，那么下面的最小割树的性质定理就无法证明

原图上u,v两点最小割就是最小割树上u到v的路径上权值最小的边

最小割树的构造

根据定义：树上去掉(s,t)后产生的两个集合恰好是原图上(s,t)的最小割把原图分成的两个集合。

我们可以直接按定义构造最小割树

最小割树的构造是递归实现的。

在当前点集随意选取两个点u,v，在原图上跑出他们之间的最小割，然后就在树上连一条从u到v,权值为\(\lambda(u,v)\)的边。

然后找出u,v分属的两个点集，对这两个点集递归进行操作。当点集中的点只剩一个的时候停止递归

时间复杂度\(O(n^3m)\)，但很难卡满（实际上就是跑了n次dinic)

  1. int node[maxv];//node[i]里面存储点的编号
  2. int tmp1[maxv],tmp2[maxv];
  3. void build(int l,int r){
  4.         if(l==r) return;
  5.         int s=node[l],t=node[l+1];//任选两个点
  6.         int cut=network_flow::dinic(s,t);
  7.         add_edge(s,t,cut);
  8.         int cnt1=0,cnt2=0;
  9.         for(int i=l;i<=r;i++){
  10.             if(network_flow::deep[node[i]]) tmp1[++cnt1]=node[i];
  11.             else tmp2[++cnt2]=node[i];
  12.             //考虑dinic算法中的最后一次bfs,因为现在残量网络上s到达不了t,所以bfs访问到的点就是s所在的点集，它们的deep不0
  13.         }
  14.         for(int i=l;i<=l+cnt1-1;i++) node[i]=tmp1[i-l+1];
  15.         for(int i=l+cnt1;i<=r;i++) node[i]=tmp2[i-cnt1-l+1];
  16.         build(l,l+cnt1-1);
  17.         build(l+cnt1,r);
  18.     }

最小割树的查询

最小割树满足一个重要的性质：

原图上u,v两点最小割就是最小割树上u到v的路径上权值最小的边

因此我们直接对建出的最小割树进行树上倍增即可

该性质的正确性证明见下方

正确性证明

为了下文描述方便，我们定义\(\lambda (a,b)\)表示a,b的最小割的权值

引理1 对于任意\(p \in V_x,q \in V_y\)，有$\lambda(x,y) \geq \lambda(p,q) $

证明：

​ 假设$\lambda(x,y) < \lambda(p,q) $,那么用割断(x,y)的代价割不断(p,q),而p与x联通，p与y联通，那么(x,y)就割不断了，这与最小割的定义矛盾，因此引理成立。

定理1 :对于任意不同的三点\(a,b,c\), \(\lambda(a,b) \geq min(\lambda(a,c),\lambda(c,b))\)

证明：考虑\(\lambda(a,b) \ , \lambda(a,c)\ ,\lambda(c,b)\)中最小的一对，不妨设为\(\lambda(a,b)\)

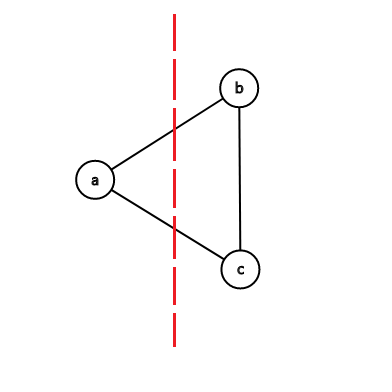
再讨论c在删掉(a,b)的割边之后与a联通还是与b联通，不妨设为与b，另一种同理。由引理1：\(\lambda(a,c) \leq \lambda(a,b)\)

又因为我们之前假设过\(\lambda(a,b)\)是最小的，因此\(\lambda(a,c) \geq \lambda(a,b)\),所以\(\lambda(a,c)=\lambda(a,b)\)

因此\(\lambda(a,b) \ , \lambda(a,c)\ ,\lambda(c,b)\)中一定有两个较小值，一个较大值。

若\(\lambda(a,b)\)是小的，则\(\lambda(a,c),\lambda(c,b)\)中一个较大的,一个较小的，取min之后还是较小值，定理显然成立

若\(\lambda(a,b)\)是大的，则\(\lambda(a,c),\lambda(c,b)\)均是较小值，定理显然成立

定理1的推论 对于任意不同的两点u,v, \(\lambda(u,v) \geq min(\lambda(u,w_1),\lambda(w_1,w_2),\lambda(w_2,w_3) \dots , \lambda(w_k,v))\)

定理2 对于任意不同的两点x,y,令p,q为最小割树x到y路径上的两点，且\(\lambda(p,q)\)最小，那么\(\lambda(p,q)=\lambda(x,y)\).也就是说，u,v两点最小割就是最小割树上u到v的路径上权值最小的边

由定理1的推论可知\(\lambda(x,y) \geq \lambda(p,q)\)

又根据最小割树的定义，x,y在p,q最小割的两侧，则\(\lambda(p,q) \geq \lambda(x,y)\)

因此\(\lambda(x,y)=\lambda(p,q)\)

题目

首先是模板

https://www.luogu.org/problemnew/show/P4897

  1. #include<iostream>
  2. #include<cstdio>
  3. #include<cstring>
  4. #include<queue>
  5. #include<cmath>
  6. #define INF 0x3f3f3f3f
  7. #define maxv 505
  8. #define maxe 1505
  9. #define maxlogv 10
  10. using namespace std;
  11. int n,m,q;
  12. namespace network_flow{
  13.     struct edge{
  14.         int from;
  15.         int to;
  16.         int next;
  17.         int flow;
  18.     }E[maxe<<2];
  19.     int head[maxv];
  20.     int deep[maxv];
  21.     int sz=1;
  22.     void add_edge(int u,int v,int w){
  23.         sz++;
  24.         E[sz].from=u;
  25.         E[sz].to=v;
  26.         E[sz].next=head[u];
  27.         E[sz].flow=w;
  28.         head[u]=sz;
  29.         sz++;
  30.         E[sz].from=v;
  31.         E[sz].to=u;
  32.         E[sz].next=head[v];
  33.         E[sz].flow=0;
  34.         head[v]=sz;
  35.     }
  36.     bool bfs(int s,int t){
  37.         memset(deep,0,sizeof(deep));
  38.         deep[s]=1;
  39.         queue<int>q;
  40.         q.push(s);
  41.         while(!q.empty()){
  42.             int x=q.front();
  43.             q.pop();
  44.             for(int i=head[x];i;i=E[i].next){
  45.                 int y=E[i].to;
  46.                 if(!deep[y]&&E[i].flow){
  47.                     deep[y]=deep[x]+1;
  48.                     q.push(y);
  49.                 }
  50.             }
  51.         }
  52.         return deep[t]!=0;
  53.     }
  54.     int dfs(int x,int t,int minf){
  55.         if(x==t) return minf;
  56.         int k,rest=minf;
  57.         for(int i=head[x];i;i=E[i].next){
  58.             int y=E[i].to;
  59.             if(deep[y]==deep[x]+1&&E[i].flow){
  60.                 k=dfs(y,t,min(rest,E[i].flow));
  61.                 rest-=k;
  62.                 E[i].flow-=k;
  63.                 E[i^1].flow+=k;
  64.                 if(k==0) deep[y]=0;
  65.                 if(rest==0) break;
  66.             }
  67.         }
  68.         return minf-rest;
  69.     }
  70.     void init(){
  71.         for(int i=2;i<=sz;i+=2){
  72.             E[i].flow=(E[i].flow+E[i^1].flow);
  73.             E[i^1].flow=0;
  74.         }
  75.     }
  76.     int dinic(int s,int t){
  77.         init();
  78.         int ans=0,now=0;
  79.         while(bfs(s,t)){
  80.             while(now=dfs(s,t,INF)) ans+=now;
  81.         }
  82.         return ans;
  83.     }
  85. } 
  87. namespace mincut_tree{
  88.     struct edge{
  89.         int from;
  90.         int to;
  91.         int next;
  92.         int len;
  93.     }E[maxv<<1];
  94.     int head[maxv];
  95.     int sz=1;
  96.     void add_edge(int u,int v,int w){
  97. //		printf("tree: %d->%d len=%d\n",u,v,w);
  98.         sz++;
  99.         E[sz].from=u;
  100.         E[sz].to=v;
  101.         E[sz].next=head[u];
  102.         E[sz].len=w;
  103.         head[u]=sz;
  104.         sz++;
  105.         E[sz].from=v;
  106.         E[sz].to=u;
  107.         E[sz].next=head[v];
  108.         E[sz].len=w;
  109.         head[v]=sz;
  110.     }
  112.     int node[maxv];
  113.     int tmp1[maxv],tmp2[maxv];
  114.     void build(int l,int r){
  115.         if(l==r) return;
  116.         int s=node[l],t=node[l+1];
  117.         int cut=network_flow::dinic(s,t);
  118.         add_edge(s,t,cut);
  119.         int cnt1=0,cnt2=0;
  120.         for(int i=l;i<=r;i++){
  121.             if(network_flow::deep[node[i]]) tmp1[++cnt1]=node[i];
  122.             else tmp2[++cnt2]=node[i];
  123.         }
  124.         for(int i=l;i<=l+cnt1-1;i++) node[i]=tmp1[i-l+1];
  125.         for(int i=l+cnt1;i<=r;i++) node[i]=tmp2[i-cnt1-l+1];
  126.         build(l,l+cnt1-1);
  127.         build(l+cnt1,r);
  128.     }
  130.     int log2n;
  131.     int deep[maxv];
  132.     int anc[maxv][maxlogv];
  133.     int minl[maxv][maxlogv];
  134.     void dfs(int x,int fa){
  135.         deep[x]=deep[fa]+1;
  136.         for(int i=1;i<=log2n;i++){
  137.             anc[x][i]=anc[anc[x][i-1]][i-1];
  138.             minl[x][i]=min(minl[x][i-1],minl[anc[x][i-1]][i-1]);
  139.         }
  140.         for(int i=head[x];i;i=E[i].next){
  141.             int y=E[i].to;
  142.             if(y!=fa){
  143.                 anc[y][0]=x;
  144.                 minl[y][0]=E[i].len;
  145.                 dfs(y,x);
  146.             }
  147.         }
  148.     }
  150.     void work(){
  151.         log2n=log2(n)+1;
  152.         for(int i=1;i<=n;i++) node[i]=i;
  153.         build(1,n);
  154.         dfs(1,0);
  155.     }
  157.     int query(int x,int y){
  158.         int ans=INF;
  159.         if(deep[x]<deep[y]) swap(x,y);
  160.         for(int i=log2n;i>=0;i--){
  161.             if(deep[anc[x][i]]>=deep[y]){
  162.                 ans=min(ans,minl[x][i]);
  163.                 x=anc[x][i];
  164.             }
  165.         }
  166.         if(x==y) return ans;
  167.         for(int i=log2n;i>=0;i--){
  168.             if(anc[x][i]!=anc[y][i]){
  169.                 ans=min(ans,minl[x][i]);
  170.                 ans=min(ans,minl[y][i]);
  171.                 x=anc[x][i];
  172.                 y=anc[y][i];
  173.             }
  174.         }
  175.         ans=min(ans,minl[x][0]);
  176.         ans=min(ans,minl[y][0]);
  177.         return ans;
  178.     }
  179. }
  181. int main(){
  182.     int u,v,w;
  183.     scanf("%d %d",&n,&m);
  184.     for(int i=1;i<=m;i++){
  185.         scanf("%d %d %d",&u,&v,&w);
  186.         network_flow::add_edge(u,v,w);
  187.         network_flow::add_edge(v,u,w);
  188.     }
  189.     mincut_tree::work();
  190.     scanf("%d",&q);
  191.     for(int i=1;i<=q;i++){
  192.         scanf("%d %d",&u,&v);
  193.         int ans=mincut_tree::query(u,v);
  194.         if(ans==INF) ans=-1;
  195.         printf("%d\n",ans);
  196.     }
  197. }

以及两道例题

[CQOI2016]不同的最小割

https://www.luogu.org/problemnew/show/P4123

先建出最小割树，然后枚举所有点对，将求出的最小割值存入一个STL set

  1. #include<iostream>
  2. #include<cstdio>
  3. #include<cstring>
  4. #include<queue>
  5. #include<cmath>
  6. #include<set>
  7. #define INF 0x3f3f3f3f
  8. #define maxv 855
  9. #define maxe 8505
  10. #define maxlogv 15
  11. using namespace std;
  12. int n,m,q;
  13. namespace network_flow{
  14.     struct edge{
  15.         int from;
  16.         int to;
  17.         int next;
  18.         int flow;
  19.     }E[maxe<<2];
  20.     int head[maxv];
  21.     int deep[maxv];
  22.     int sz=1;
  23.     void add_edge(int u,int v,int w){
  24.         sz++;
  25.         E[sz].from=u;
  26.         E[sz].to=v;
  27.         E[sz].next=head[u];
  28.         E[sz].flow=w;
  29.         head[u]=sz;
  30.         sz++;
  31.         E[sz].from=v;
  32.         E[sz].to=u;
  33.         E[sz].next=head[v];
  34.         E[sz].flow=0;
  35.         head[v]=sz;
  36.     }
  37.     bool bfs(int s,int t){
  38.         memset(deep,0,sizeof(deep));
  39.         deep[s]=1;
  40.         queue<int>q;
  41.         q.push(s);
  42.         while(!q.empty()){
  43.             int x=q.front();
  44.             q.pop();
  45.             for(int i=head[x];i;i=E[i].next){
  46.                 int y=E[i].to;
  47.                 if(!deep[y]&&E[i].flow){
  48.                     deep[y]=deep[x]+1;
  49.                     q.push(y);
  50.                 }
  51.             }
  52.         }
  53.         return deep[t]!=0;
  54.     }
  55.     int dfs(int x,int t,int minf){
  56.         if(x==t) return minf;
  57.         int k,rest=minf;
  58.         for(int i=head[x];i;i=E[i].next){
  59.             int y=E[i].to;
  60.             if(deep[y]==deep[x]+1&&E[i].flow){
  61.                 k=dfs(y,t,min(rest,E[i].flow));
  62.                 rest-=k;
  63.                 E[i].flow-=k;
  64.                 E[i^1].flow+=k;
  65.                 if(k==0) deep[y]=0;
  66.                 if(rest==0) break;
  67.             }
  68.         }
  69.         return minf-rest;
  70.     }
  71.     void init(){
  72.         for(int i=2;i<=sz;i+=2){
  73.             E[i].flow=(E[i].flow+E[i^1].flow);
  74.             E[i^1].flow=0;
  75.         }
  76.     }
  77.     int dinic(int s,int t){
  78.         init();
  79.         int ans=0,now=0;
  80.         while(bfs(s,t)){
  81.             while(now=dfs(s,t,INF)) ans+=now;
  82.         }
  83.         return ans;
  84.     }
  86. } 
  88. namespace mincut_tree{
  89.     struct edge{
  90.         int from;
  91.         int to;
  92.         int next;
  93.         int len;
  94.     }E[maxv<<1];
  95.     int head[maxv];
  96.     int sz=1;
  97.     void add_edge(int u,int v,int w){
  98. //		printf("tree: %d->%d len=%d\n",u,v,w);
  99.         sz++;
  100.         E[sz].from=u;
  101.         E[sz].to=v;
  102.         E[sz].next=head[u];
  103.         E[sz].len=w;
  104.         head[u]=sz;
  105.         sz++;
  106.         E[sz].from=v;
  107.         E[sz].to=u;
  108.         E[sz].next=head[v];
  109.         E[sz].len=w;
  110.         head[v]=sz;
  111.     }
  113.     int node[maxv];
  114.     int tmp1[maxv],tmp2[maxv];
  115.     void build(int l,int r){
  116.         if(l==r) return;
  117.         int s=node[l],t=node[l+1];
  118.         int cut=network_flow::dinic(s,t);
  119.         add_edge(s,t,cut);
  120.         int cnt1=0,cnt2=0;
  121.         for(int i=l;i<=r;i++){
  122.             if(network_flow::deep[node[i]]) tmp1[++cnt1]=node[i];
  123.             else tmp2[++cnt2]=node[i];
  124.         }
  125.         for(int i=l;i<=l+cnt1-1;i++) node[i]=tmp1[i-l+1];
  126.         for(int i=l+cnt1;i<=r;i++) node[i]=tmp2[i-cnt1-l+1];
  127.         build(l,l+cnt1-1);
  128.         build(l+cnt1,r);
  129.     }
  131.     int log2n;
  132.     int deep[maxv];
  133.     int anc[maxv][maxlogv];
  134.     int minl[maxv][maxlogv];
  135.     void dfs(int x,int fa){
  136.         deep[x]=deep[fa]+1;
  137.         for(int i=1;i<=log2n;i++){
  138.             anc[x][i]=anc[anc[x][i-1]][i-1];
  139.             minl[x][i]=min(minl[x][i-1],minl[anc[x][i-1]][i-1]);
  140.         }
  141.         for(int i=head[x];i;i=E[i].next){
  142.             int y=E[i].to;
  143.             if(y!=fa){
  144.                 anc[y][0]=x;
  145.                 minl[y][0]=E[i].len;
  146.                 dfs(y,x);
  147.             }
  148.         }
  149.     }
  151.     void work(){
  152.         log2n=log2(n)+1;
  153.         for(int i=1;i<=n;i++) node[i]=i;
  154.         build(1,n);
  155.         dfs(1,0);
  156.     }
  158.     int query(int x,int y){
  159.         int ans=INF;
  160.         if(deep[x]<deep[y]) swap(x,y);
  161.         for(int i=log2n;i>=0;i--){
  162.             if(deep[anc[x][i]]>=deep[y]){
  163.                 ans=min(ans,minl[x][i]);
  164.                 x=anc[x][i];
  165.             }
  166.         }
  167.         if(x==y) return ans;
  168.         for(int i=log2n;i>=0;i--){
  169.             if(anc[x][i]!=anc[y][i]){
  170.                 ans=min(ans,minl[x][i]);
  171.                 ans=min(ans,minl[y][i]);
  172.                 x=anc[x][i];
  173.                 y=anc[y][i];
  174.             }
  175.         }
  176.         ans=min(ans,minl[x][0]);
  177.         ans=min(ans,minl[y][0]);
  178.         return ans;
  179.     }
  180. }
  182. set<int>S;
  183. int main(){
  184.     int u,v,w;
  185.     scanf("%d %d",&n,&m);
  186.     for(int i=1;i<=m;i++){
  187.         scanf("%d %d %d",&u,&v,&w);
  188.         network_flow::add_edge(u,v,w);
  189.         network_flow::add_edge(v,u,w);
  190.     }
  191.     mincut_tree::work();
  192.     for(int i=1;i<=n;i++){
  193.         for(int j=i+1;j<=n;j++){
  194.             S.insert(mincut_tree::query(i,j));
  195.         }
  196.     }
  197.     printf("%d\n",S.size());
  198. }

[ZJOI2011]最小割

https://www.luogu.org/problemnew/show/P4123

先建出最小割树，然后枚举所有点对，将求出的最小割值排序，然后二分查找就可以了

  1. //BZOJ 2229
  2. #include<iostream>
  3. #include<cstdio>
  4. #include<cstring>
  5. #include<queue>
  6. #include<cmath>
  7. #include<algorithm>
  8. #define INF 0x3f3f3f3f
  9. #define maxv 155
  10. #define maxe 3005
  11. #define maxlogv 10
  12. using namespace std;
  13. int n,m,q;
  14. namespace network_flow {
  15.     struct edge {
  16.         int from;
  17.         int to;
  18.         int next;
  19.         int flow;
  20.     } E[maxe<<2];
  21.     int head[maxv];
  22.     int deep[maxv];
  23.     int sz=1;
  24.     void add_edge(int u,int v,int w) {
  25.         sz++;
  26.         E[sz].from=u;
  27.         E[sz].to=v;
  28.         E[sz].next=head[u];
  29.         E[sz].flow=w;
  30.         head[u]=sz;
  31.         sz++;
  32.         E[sz].from=v;
  33.         E[sz].to=u;
  34.         E[sz].next=head[v];
  35.         E[sz].flow=0;
  36.         head[v]=sz;
  37.     }
  38.     bool bfs(int s,int t) {
  39.         memset(deep,0,sizeof(deep));
  40.         deep[s]=1;
  41.         queue<int>q;
  42.         q.push(s);
  43.         while(!q.empty()) {
  44.             int x=q.front();
  45.             q.pop();
  46.             for(int i=head[x]; i; i=E[i].next) {
  47.                 int y=E[i].to;
  48.                 if(!deep[y]&&E[i].flow) {
  49.                     deep[y]=deep[x]+1;
  50.                     q.push(y);
  51.                 }
  52.             }
  53.         }
  54.         return deep[t]!=0;
  55.     }
  56.     int dfs(int x,int t,int minf) {
  57.         if(x==t) return minf;
  58.         int k,rest=minf;
  59.         for(int i=head[x]; i; i=E[i].next) {
  60.             int y=E[i].to;
  61.             if(deep[y]==deep[x]+1&&E[i].flow) {
  62.                 k=dfs(y,t,min(rest,E[i].flow));
  63.                 rest-=k;
  64.                 E[i].flow-=k;
  65.                 E[i^1].flow+=k;
  66.                 if(k==0) deep[y]=0;
  67.                 if(rest==0) break;
  68.             }
  69.         }
  70.         return minf-rest;
  71.     }
  72.     void init() {
  73.         for(int i=2; i<=sz; i+=2) {
  74.             E[i].flow=(E[i].flow+E[i^1].flow);
  75.             E[i^1].flow=0;
  76.         }
  77.     }
  78.     int dinic(int s,int t) {
  79.         init();
  80.         int ans=0,now=0;
  81.         while(bfs(s,t)) {
  82.             while(now=dfs(s,t,INF)) ans+=now;
  83.         }
  84.         return ans;
  85.     }
  87. }
  89. namespace mincut_tree {
  90.     struct edge {
  91.         int from;
  92.         int to;
  93.         int next;
  94.         int len;
  95.     } E[maxv<<1];
  96.     int head[maxv];
  97.     int sz=1;
  98.     void add_edge(int u,int v,int w) {
  99. //		printf("tree: %d->%d len=%d\n",u,v,w);
  100.         sz++;
  101.         E[sz].from=u;
  102.         E[sz].to=v;
  103.         E[sz].next=head[u];
  104.         E[sz].len=w;
  105.         head[u]=sz;
  106.         sz++;
  107.         E[sz].from=v;
  108.         E[sz].to=u;
  109.         E[sz].next=head[v];
  110.         E[sz].len=w;
  111.         head[v]=sz;
  112.     }
  114.     int node[maxv];
  115.     int tmp1[maxv],tmp2[maxv];
  116.     void build(int l,int r) {
  117.         if(l==r) return;
  118.         int s=node[l],t=node[l+1];
  119.         int cut=network_flow::dinic(s,t);
  120.         add_edge(s,t,cut);
  121.         int cnt1=0,cnt2=0;
  122.         for(int i=l; i<=r; i++) {
  123.             if(network_flow::deep[node[i]]) tmp1[++cnt1]=node[i];
  124.             else tmp2[++cnt2]=node[i];
  125.         }
  126.         for(int i=l; i<=l+cnt1-1; i++) node[i]=tmp1[i-l+1];
  127.         for(int i=l+cnt1; i<=r; i++) node[i]=tmp2[i-l-cnt1+1];
  128.         build(l,l+cnt1-1);
  129.         build(l+cnt1,r);
  130.     }
  132.     int log2n;
  133.     int deep[maxv];
  134.     int anc[maxv][maxlogv];
  135.     int minl[maxv][maxlogv];
  136.     void dfs(int x,int fa) {
  137. //		printf("dfs on %d\n",x);
  138.         deep[x]=deep[fa]+1;
  139.         for(int i=1; i<=log2n; i++) {
  140.             anc[x][i]=anc[anc[x][i-1]][i-1];
  141.             minl[x][i]=min(minl[x][i-1],minl[anc[x][i-1]][i-1]);
  142.         }
  143.         for(int i=head[x]; i; i=E[i].next) {
  144.             int y=E[i].to;
  145.             if(y!=fa) {
  146.                 anc[y][0]=x;
  147.                 minl[y][0]=E[i].len;
  148.                 dfs(y,x);
  149.             }
  150.         }
  151.     }
  153.     void work() {
  155.         sz=1;
  156.         memset(E,0,sizeof(E));
  157.         memset(head,0,sizeof(head));
  158.         log2n=log2(n)+1;
  159.         for(int i=1; i<=n; i++) node[i]=i;
  160.         memset(deep,0,sizeof(deep));
  161.         memset(anc,0,sizeof(anc));
  162.         memset(minl,0,sizeof(minl));
  163.         build(1,n);
  164. //		printf("buildok");
  165.         dfs(1,0);
  166.     }
  168.     int query(int x,int y) {
  169.         int ans=INF;
  170.         if(deep[x]<deep[y]) swap(x,y);
  171.         for(int i=log2n; i>=0; i--) {
  172.             if(deep[anc[x][i]]>=deep[y]) {
  173.                 ans=min(ans,minl[x][i]);
  174.                 x=anc[x][i];
  175.             }
  176.         }
  177.         if(x==y) return ans;
  178.         for(int i=log2n; i>=0; i--) {
  179.             if(anc[x][i]!=anc[y][i]) {
  180.                 ans=min(ans,minl[x][i]);
  181.                 ans=min(ans,minl[y][i]);
  182.                 x=anc[x][i];
  183.                 y=anc[y][i];
  184.             }
  185.         }
  186.         ans=min(ans,minl[x][0]);
  187.         ans=min(ans,minl[y][0]);
  188.         return ans;
  189.     }
  190. }
  192. int cases;
  193. int pc;
  194. int ans[maxv*maxv/2];
  195. int main() {
  196. #ifdef FILE_IO
  197.     freopen("1.in","r",stdin);
  198. #endif
  199.     int u,v,w;
  200.     scanf("%d",&cases);
  201.     while(cases--) {
  202.         memset(network_flow::head,0,sizeof(network_flow::head));
  203.         memset(network_flow::E,0,sizeof(network_flow::E));
  204.         network_flow::sz=1;
  205.         scanf("%d %d",&n,&m);
  206.         for(int i=1; i<=m; i++) {
  207.             scanf("%d %d %d",&u,&v,&w);
  208.             network_flow::add_edge(u,v,w);
  209.             network_flow::add_edge(v,u,w);
  210.         }
  211.         mincut_tree::work();
  212.         pc=0;
  213.         for(int i=1;i<=n;i++){
  214.             for(int j=i+1;j<=n;j++){
  215.                 ans[++pc]=mincut_tree::query(i,j);
  216.             }
  217.         }
  218.         sort(ans+1,ans+1+pc);
  219.         scanf("%d",&q);
  220.         for(int i=1; i<=q; i++) {
  221.             scanf("%d",&w);
  222.             printf("%d\n",upper_bound(ans+1,ans+1+pc,w)-ans-1);
  223.         }
  224.         printf("\n");
  225.     }
  226. }

最小割树(Gomory-Hu Tree)求无向图最小割详解 附 BZOJ2229,BZOJ4519题解的更多相关文章

  1. 最小割树Gomory–Hu tree

    fanhq666地址:http://fanhq666.blog.163.com/blog/static/8194342620113495335724/ wiki地址(证明):https://en.wi ...

  2. bzoj 4519: [Cqoi2016]不同的最小割【最小割树Gomory–Hu tree】

    算法详见:http://www.cnblogs.com/lokiii/p/8191573.html 求出点两两之间的最小割之后,把他们扔到map/set里跑即可 可怕的是map和set跑的时间竟然完全 ...

  3. bzoj 2229: [Zjoi2011]最小割【Gomory–Hu tree最小割树】

    这个算法详见http://www.cnblogs.com/lokiii/p/8191573.html 求出两两之间最小割之后暴力统计即可 #include<iostream> #inclu ...

  4. [学习笔记]最小割树（Gomory-Hu Tree）

    最小割树(\(\mathcal{Gomory-Hu Tree}\))简明指南 对于单源最短路径,我们有\(SPFA\)和\(Dijkstra\),对于多源最短路径,我们有\(Floyd\):对于两点间 ...

  5. 【模板】最小割树（Gomory-Hu Tree）

    传送门 Description 给定一个\(n\)个点\(m\)条边的无向连通图,多次询问两点之间的最小割 两点间的最小割是这样定义的:原图的每条边有一个割断它的代价,你需要用最小的代价使得这两个点不 ...

  6. BZOJ 1185: [HNOI2007]最小矩形覆盖-旋转卡壳法求点集最小外接矩形(面积)并输出四个顶点坐标-备忘板子

    来源:旋转卡壳法求点集最小外接矩形(面积)并输出四个顶点坐标 BZOJ又崩了,直接贴一下人家的代码. 代码: #include"stdio.h" #include"str ...

  7. 求双连通分量的详解。（根据刘汝佳的训练指南p314）

    无向图的双连通分量 点-双连通图:一个连通的无向图内部没有割点,那么该图是点-双连通图.         注意:孤立点,以及两点一边这两种图都是点-双连通的.因为它们都是内部无割点. 边-双连通图:一 ...

  8. HDU1542-Atlantis【离散化&线段树&扫描线】个人认为很全面的详解

    刚上大一的时候见过这种题,感觉好牛逼哇,这都能算 如今已经不打了,不过适当写写题保持思维活跃度还是不错的,又碰到这种题了,想把它弄出来 说实话,智商不够,看了很多解析,花了4.5个小时才弄明白 网上好 ...

  9. HDU 1003 Max Sum【动态规划求最大子序列和详解 】

    Max Sum Time Limit: 2000/1000 MS (Java/Others)    Memory Limit: 65536/32768 K (Java/Others)Total Sub ...

随机推荐

  1. vue路由守卫配合权限，白名单

    router.beforeEach(async(to, from, next) => { // 进度条开始 NProgress.start() // 确认用户是否已登录(获取它的token值,这 ...

  2. ASE Alpha Sprint - backend scrum 2

    本次scrum于2019.11.5再sky garden进行,持续30分钟. 参与人: Zhikai Chen, Jia Ning, Haifeng Chen, Hao Wang 请假: Xin Ka ...

  3. Winfrom中数据的双向绑定(使用INotifyPropertyChanged)

    在WPF中新建项目是自动实现了INotifyPropertyChanged接口,用于数据绑定时非常的方便在winfrom中也可以实现INotifyPropertyChanged接口 将需要绑定的字段写 ...

  4. Airbnb JavaScript 编码风格指南（2018年最新版）

    原网址 :  https://segmentfault.com/a/1190000013040555 类型 基本类型:直接存取 string number boolean null undefined ...

  5. node npm vue.js 笔记

    cnpm 下载包的速度更快一些. 地址:http://npm.taobao.org/ 安装cnpm: npm install -g cnpm --registry=https://registry.n ...

  6. Windows 10 系统获取密钥方法

    方法一: 快捷键 win+R 打开运行窗口,输入 regedit 打开注册表编辑器,选择 HKEY_LOCAL_MACHINE\SOFTWARE\Microsoft\Windows NT\Curren ...

  7. django classonlymethod 和 python classmethod的区别

    --classmethod可以被一个实例调用,classonlyethod只能被类调用 class Kls(object): no_inst = 0 def __init__(self): Kls.n ...

  8. java Main方法 获取 maven 的resource 下的xml文件

    Properties properties = new Properties(); File file = new File("src/main/resources/generator.xm ...

  9. App中h5音频不能播放问题

    前置:以下问题是针对vue项目的解决方案 问题一:IOS中音频不能自动播放 原因:ios禁止了音频自动播放 解决办法:在vue的生命周期mounted中获取音频Dom并调用音频播放方法play(),注 ...

  10. Best Practices For Running On The PS4

    原文:https://forums.unrealengine.com/showthread.php?54448-Best-Practices-For-Running-On-The-PS4 Hey gu ...