qbzt day6 下午 模拟赛

我太菜了

T2

给定一张有向图，每个点有点权。试找到一条路径，使得该路径上的点权最

大值减去点权最小值最大，问这个差最大是多少。

 

话说这个题第一个想到的思路是tarjan缩点+拓扑排序来着。。。

这个思路是对的，可惜太难写。。。

我自己的错误思路就不放上了，

 

这个题正解竟然是bfs

只需要找出从最大点走到最小点或者从最小点走到最大点就行了

考虑从每个点出发能走到的所有点当中最小的点是多少以及从这个点向回走的的最小值

枚举每一个点作为起点或者终点

答案只有两种情况：min->max    max->min

直接枚举max是哪个点

对于每个点正着bfs并且反着bfs就好了

优化：对于每个点算他正着走和反着走的答案，每次都bfs是算法慢的原因。我们发现先算1号点再算2号点和倒过来是一样的

所以我们直接把点权从小到大排序，然后一个点一个点去处理所有的答案

如果最小的点能到这个点那这个点一定是从自己开始向前走最小的点。

直接标记一下这个点向前走最小的点是多少

也就是bfs的过程只需要bfs到没有算过答案的点就好了，同理这个点能到达的所有点都不用被算了。在这种方法下每个点只会被bfs一次

代码：

#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<algorithm>
#include<queue>

using namespace std;

const int maxn=;
const int maxm=;

int n,m,en,result[maxn],z[maxn],y[maxn];

struct edge
{
    int s,e;
    bool rev;
    edge *next;
}*v[maxn],ed[maxm<<];

void add_edge(int s,int e)
{
    en++;
    ed[en].next=v[s];v[s]=ed+en;v[s]->e=e;v[s]->rev=false;
    en++;
    ed[en].next=v[e];v[e]=ed+en;v[e]->e=s;v[s]->rev=true;
} //直接双向建边，因为bfs要两边跑。不过要注意标记哪一条真实存在 

bool cmp(int a,int b)
{
    return z[a]<z[b];
}

void bfs(int p)
{
    queue<int> q;
    if (!result[p]) result[p]=z[p];//表示已经有答案了
    q.push(p);
    while (q.size())
    {
        int now=q.front();
        q.pop();
        for (edge *e=v[now];e;e=e->next)
            if (!e->rev && !result[e->e])//遍历真实存在的边
            {
                result[e->e]=z[p];
                q.push(e->e);
            }
    }
    q.push(p);
    while (q.size())
    {
        int now=q.front();
        q.pop();
        for (edge *e=v[now];e;e=e->next)
            if (e->rev && !result[e->e])//遍历反着的边
            {
                result[e->e]=z[p];
                q.push(e->e);
            }
    }
}

int main()
{
    scanf("%d%d",&n,&m);
    for (int a=;a<=n;a++)
        scanf("%d",&z[a]);
    for (int a=;a<=m;a++)
    {
        int s,e;
        scanf("%d%d",&s,&e);
        add_edge(s,e);
    }
    for (int a=;a<=n;a++)
        y[a]=a;
    sort(y+,y+n+,cmp);
    for (int a=;a<=n;a++)
        bfs(y[a]);
    int ans=;
    for (int a=;a<=n;a++)
       ans=max(ans,z[a]-result[a]);
    printf("%d\n",ans);

    return ;
}

T3

有N个人，每个人都有两把刷子，每个刷子都有一个属性值。如果说一个人拿着的两把刷子的属性值之差的绝对值超过了N，则这个人无法使用他的两把刷 子。现在你可以选择交换不同人的某把刷子，使得每个人都能够使用他们的刷子问最小所需要的交换次数。

这是个很有思维难度的题。看数据范围很容易想到状压

f[s]表示s所对应的这些人之间能不能通过交换变的合法

把这些人排一个序，只需要检查能否两两组成一对就可以了

设排序之后数组为c[1],c[2],....c[2n-1],c[2n]

答案最大不超过人的个数-1，也就是n-1

每次交换至少搞定一个人

设g[s]为我要让s这些人都合法所需要的最少交换次数

如果s的二进制位上有k个1，那么答案<=k-1

初始化g[s]=k-1，代表总有一种方法是k-1，现在需要找比k-1更小的数

怎么找？N<=16告诉我们，现在应该枚举子集了。

枚举s’，剩下的部分是s^s’

如果这两个部分都能自己解决的话，答案就缩小到了n-2

那么问题就变成了：最多能把n个人分成多少个部分，使得每一个部分都能自己解决

所以g[s]也就表示最多能把s分成多少个部分使得每个部分都能自己解决

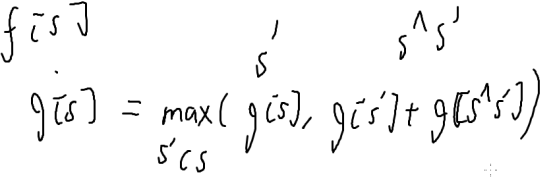
g[s]=max(g[s],g[s’]+g[s^s’]) (s’∈s)

Ans=n-g[2^n-1]