JS中的reduce函数

海纳百川，有容乃大

定义：

reduce()方法接受一个函数作为累加器，数组中的每个值（从左向右）开始缩减，最终计算为一个值。对空数组是不会执行回调函数的。

案例：

1. 计算数组总和：

   var num = [1,2,3,4,5];
   var res = num.reduce(function(total,num){
       return total+num;
       //return total + Math.round(num);//对数组元素四舍五入并计算总和
   },0);
   console.log(res)；//
   //num.reduce((total,num) => total += num, 0);
   //没有初始值initialValue（即上面例子中的0），当数组为0时会抛出异常提示reduce函数没有初始值，所以为兼容性一般加上initialValue

2. 合并二维数组

   var red = [[0, 1], [2, 3], [4, 5]].reduce(function(a, b) {
    return a.concat(b);
   }, []);
   console.log(red)
   VM291:4 (6) [0, 1, 2, 3, 4, 5]

3. 统计一个数组中有多少个不重复的单词

   不用reduce时：
   var arr = ["apple","orange","apple","orange","pear","orange"];
   function getWordCnt(){
     var obj = {};
     for(var i= 0, l = arr.length; i< l; i++){
       var item = arr[i];
       obj[item] = (obj[item] +1 ) || 1;
     }
     return obj;
   }
   console.log(getWordCnt());
   VM3704:14 {apple: 2, orange: 3, pear: 1}
   
   用reduce时：
   var arr = ["apple","orange","apple","orange","pear","orange"];
   function getWordCnt(){
     return arr.reduce(function(prev,next){
       prev[next] = (prev[next] + 1) || 1;
       return prev;
     },{});
   }
   console.log(getWordCnt());
   VM3704:14 {apple: 2, orange: 3, pear: 1}

理解：

reduce（callback,initialValue)会传入两个参数，回调函数（callback）和初始值（initialValue）。当没有传入初始值时，prev是从数组中第一个元素开始的，next是数组的第二个元素；当传入初始值（initialValue）后，第一个prev将是initialValue，next将是数组中的第一个元素。

例如：

var arr = ["apple","orange"];
function noPassValue(){
  return arr.reduce(function(prev,next){
    console.log("prev:",prev);
    console.log("next:",next);
    return prev;
  });
}

function passValue(){
  return arr.reduce(function(prev,next){
    console.log("prev:",prev);
    console.log("next:",next);
    prev[next] = 1;
    return prev;
  },{});
}
console.log("No Additional parameter:",noPassValue());
console.log("----------------");
console.log("With {} as an additional parameter:",passValue());

运行结果为：

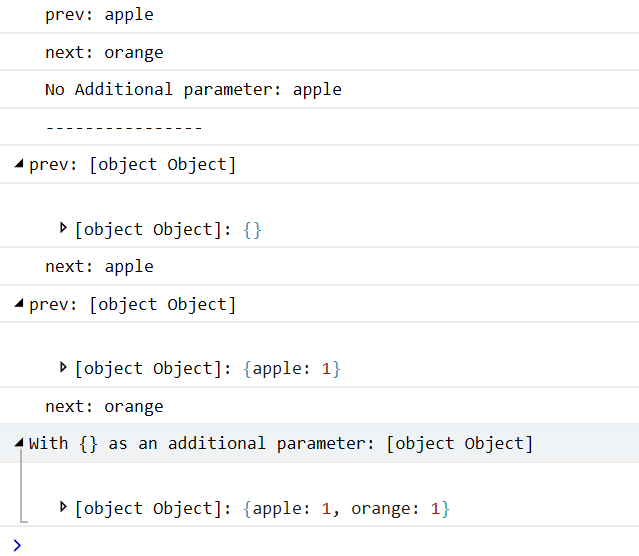
文章转载自：https://www.cnblogs.com/mafeng/p/10249887.html