[数据结构] 2.3 Trie树

抱歉更新晚了，看了几天三体，2333，我们继续数据结构之旅。

一.什么是Tire树？

Tire树有很多名字：字典树、单词查找树。 故名思意，它就是一本”字典“，当我们查找"word"单词时，先找到w开头的词汇，再继续往下找到o开头的词汇，依次类推。

特点:

　　1）除去根节点外的所有节点都有一个字符

　　2）兄弟节点的字母各不相同

　　3）从根到某一字符经过的所有字符拼接成一个 ”单词“ 或者 ”单词前缀“

例如:

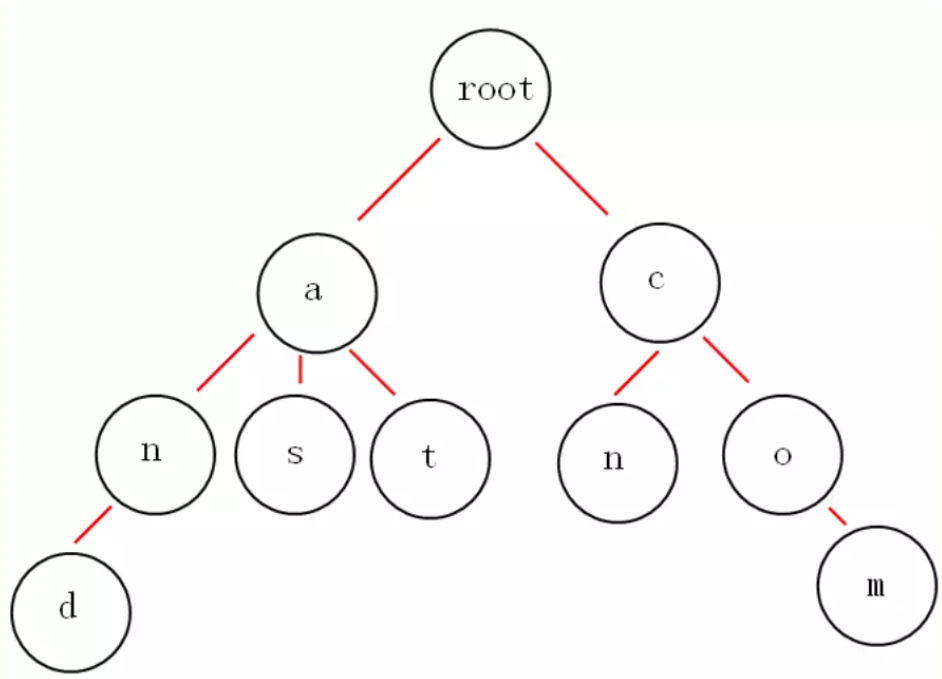
很显然，Trie是空间换时间的操作，通过字符串公共前缀降低查询开销。

二.Trie树的应用场景。

Trie树用于 前缀匹配 和 范围查找 ，这些在搜索引擎等中可以用到。

但是用来匹配字符串的话，虽然也可以但是太鸡肋了。

例子:查找10W个字符串中是否存在某些字符串。

　　思路1: 用hash分区，相同Hash值的分区进行匹配

　　思路2: 用trie树，稳定的复杂度

可现实是：

　　hash:几乎所有语言都有现成库

　　trie:你自己手写不靠谱的算法，或用一些压根不流行的包

所以用hash是99%的工程师会用的方法。至于为什么Java或其他语言不在语言库中扩展Trie：

　　1）计算机中的字符太多，ASCII中只有128，但是Unicode中有65536个

　　2）如果字符串数目过大，或者匹配的位数过多，都会占用很大的空间存储Trie树，Trie树的大小真的很可怕，这种情况下几乎不能用

三.Trie树的例子。

从10W个长度不超过10的字母的单词中，对每个单词，记录它首次出现的位置。

package ds7.trie;

public class Trie {
    /**
     * Trie树的顶点
     */
    static class Vertex{
        int firstPlace = -1;
        Vertex[] vertices = new Vertex[26];
    }

    /**
     * Trie树
     */
    static class TrieTree{
        Vertex root = new Vertex();

        /**
         * 向某个节点插入单词/单词片段
         * @param vertex
         * @param word
         */
        public void insertWord(Vertex vertex , String word, int firstPlace){
            if(word.length() < 1){
                return;
            }
            char ch = word.charAt(0);
            ch = Character.toUpperCase(ch);
            Vertex node = vertex.vertices[ch - 65];
            if(node == null){
                Vertex v = new Vertex();
                v.firstPlace = firstPlace;
                vertex.vertices[ch - 65] = v;
            }

            insertWord(vertex.vertices[ch - 65], word.substring(1), firstPlace);
        }

        /**
         * 查找第一次出现的位置
         * @param word
         * @return
         */
        public int getFirstPlace(String word){
            int result = -1;
            Vertex current = root;
            for(char ch : word.toCharArray()){
                ch = Character.toUpperCase(ch);
                Vertex tmp = current.vertices[ch - 65];
                if(tmp == null){
                    return -1;
                }else{
                    current = tmp;
                    continue;
                }
            }
            result = current.firstPlace;
            return result;
        }
    }

    public static void main(String[] args) {
        String[] words = new String[]{
          "haha","java","word","python","word","c","scala","word",
        };

        TrieTree trieTree = new TrieTree();
        for(int i = 0; i < words.length; i++){
            trieTree.insertWord(trieTree.root,words[i],i);
        }

        System.out.println("单词`word`首次出现在:" + trieTree.getFirstPlace("word"));
    }
}

result:

单词`word`首次出现在:2