【HDU6662】Acesrc and Travel【树形DP】

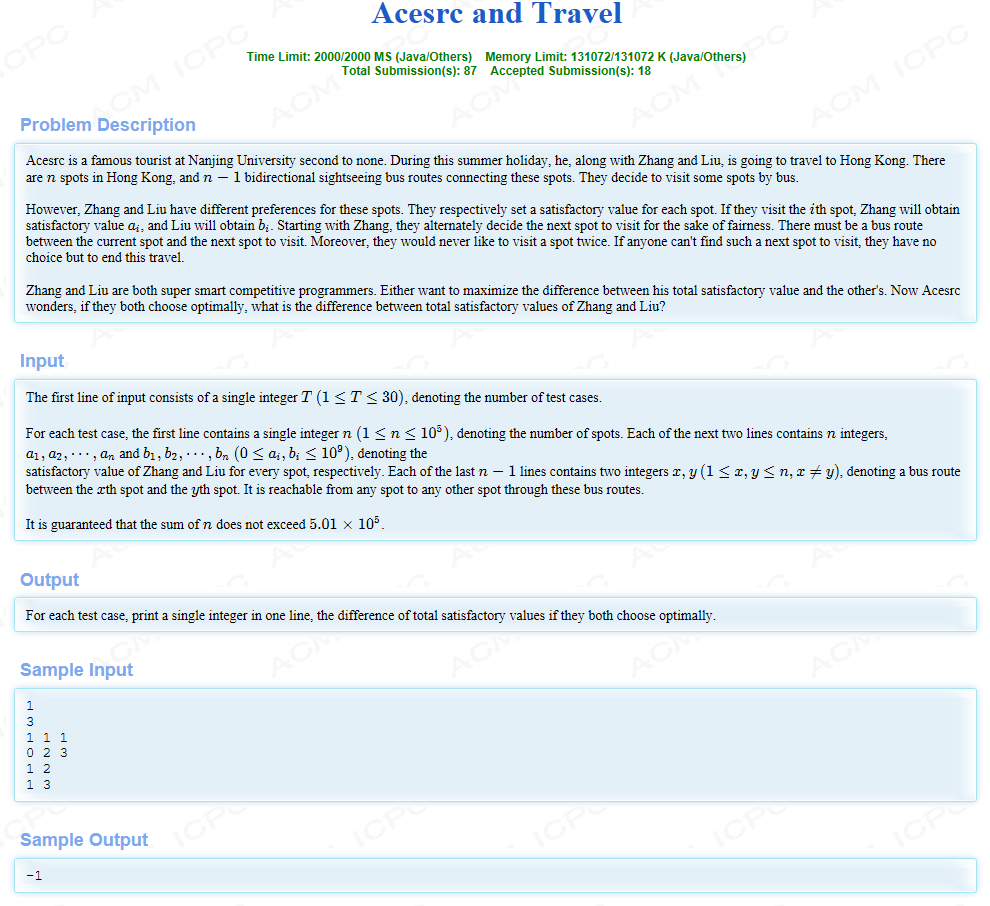
题目大意：给你一棵树，每个节点有一个权值，Alice和Bob进行博弈，起点由Alice确定，确定后交替选择下一个点，Alice目标是最终值尽可能大，Bob目标是尽可能小

题解：很明显是树形DP，那么考虑如何dp

设F[i][0/1]表示第i个点先手选/后手选的答案

那么不难想到

F[i][0]=max(F[j][1])+v[i]

F[i][1]=min(F[j][0])+v[i]

一次以1为根进行dfs可以求出选择1为根时的答案，此时考虑换根

换根时将换根前的所有状态保存下来，dfs下去之后求出其子树答案后将状态复原

换根时有两种情况，1、原根的答案是新根推过来的。2、原根的答案不是从新根推过来的

对于第二种情况很简单，我们只需要把原根当做新根的子树然后进行转移即可

考虑第一种情况，将原根变为儿子之后，其F值由除新根之外的所有儿子转移而来

于是很容易想到在原有保存最大值（最小值）的基础上再保存次大值（次小值），这样就可以O(1)更新原根的答案了

更新完后就和第二种情况一样了

代码：

#include<iostream>
#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<string>
#define ll long long
#define INF 1e18
using namespace std;
int T,n;
ll v[],f[][];
ll mx[][],mn[][];
ll ans;
int mxbh[],mnbh[];
struct node
{
    int x,y;
}tr[*];
int hd[],nxt[*],rn;
void build(int x,int y){tr[++rn]=(node){x,y};nxt[rn]=hd[x];hd[x]=rn;}
void init()
{
    rn=;
    memset(f,,sizeof(f));
    memset(hd,,sizeof(hd));
    memset(nxt,,sizeof(nxt));
}
void dfs(int now,int last)
{
    int t1=hd[now],t2;
    mx[now][]=mx[now][]=-INF;
    mn[now][]=mn[now][]=INF;
    mxbh[now]=;mnbh[now]=;
    while(t1)
    {
      t2=tr[t1].y;
      if(t2!=last)
      {
        dfs(t2,now);
        if(f[t2][]>=mx[now][]){mx[now][]=mx[now][];mx[now][]=f[t2][];mxbh[now]=t2;}
        else if(f[t2][]>mx[now][])mx[now][]=f[t2][];
        if(f[t2][]<=mn[now][]){mn[now][]=mn[now][];mn[now][]=f[t2][];mnbh[now]=t2;}
        else if(f[t2][]<mn[now][])mn[now][]=f[t2][];
      }
      t1=nxt[t1];
    }
    if(mx[now][]==-INF)mx[now][]=;
    if(mn[now][]==INF)mn[now][]=;
    //printf("%d:%lld %lld %lld\n",now,mx[now][0],mn[now][0],v[now]);
    f[now][]=mx[now][]+v[now];
    f[now][]=mn[now][]+v[now];
    //printf("%d %lld %lld %lld\n",now,f[now][1],max1,v[now]);
}
void dfs2(int now,int last)
{
    ans=max(ans,f[now][]);
    //printf("  %d\n",now);
    //for(int i=1;i<=n;i++)printf("%lld %lld:%d %d\n",f[i][0],f[i][1],mxbh[i],mnbh[i]);
    //printf(" %lld %lld|%lld %lld\n",mx[now][0],mx[now][1],mn[now][0],mn[now][1]);
    //printf("\n");
    int t1=hd[now],t2;
    ll fi0,fi1,fj0,fj1,tv,mxj0,mxj1,mnj0,mnj1;
    int mxbhi,mxbhj,mnbhi,mnbhj;
    while(t1)
    {
      t2=tr[t1].y;
      if(t2!=last)
      {
          fi0=f[now][];fi1=f[now][];
          fj0=f[t2][];fj1=f[t2][];
          mxbhi=mxbh[now];mnbhi=mnbh[now];
          mxbhj=mxbh[t2];mnbhj=mnbh[t2];
          if(mxbh[now]==t2)
          {
            tv=v[now];
          if(mx[now][]!=-INF)tv+=mx[now][];
          f[now][]=tv;
        }
        if(mnbh[now]==t2)
        {
          tv=v[now];
          if(mn[now][]!=INF)tv+=mn[now][];
          f[now][]=tv;
        }
        mxj0=mx[t2][];mxj1=mx[t2][];
        mnj0=mn[t2][];mnj1=mn[t2][];
        if(mxbhj==)mx[t2][]=-INF;
        if(mnbhj==)mn[t2][]=INF;
        if(f[now][]>=mx[t2][]){mx[t2][]=mx[t2][];mx[t2][]=f[now][];mxbh[t2]=now;}
        else if(f[now][]>mx[t2][])mx[t2][]=f[now][];
        if(f[now][]<=mn[t2][]){mn[t2][]=mn[t2][];mn[t2][]=f[now][];mnbh[t2]=now;}
        else if(f[now][]<mn[t2][])mn[t2][]=f[now][];
        f[t2][]=mx[t2][]+v[t2];
        f[t2][]=mn[t2][]+v[t2];
        dfs2(t2,now);
        f[now][]=fi0;f[now][]=fi1;
        f[t2][]=fj0;f[t2][]=fj1;
        mx[t2][]=mxj0;mx[t2][]=mxj1;
        mn[t2][]=mnj0;mn[t2][]=mnj1;
        mxbh[now]=mxbhi;mnbh[now]=mnbhi;
        mxbh[t2]=mxbhj;mnbh[t2]=mnbhj;
      }
      t1=nxt[t1];
    }
}
int main()
{
    scanf("%d",&T);
    int a,b;
    while(T--)
    {
      init();
      scanf("%d",&n);
      for(int i=;i<=n;i++)scanf("%lld",&v[i]);
      for(int i=;i<=n;i++){scanf("%d",&a);v[i]-=a;}
      for(int i=;i<n;i++)
      {
        scanf("%d%d",&a,&b);
        build(a,b);build(b,a);
      }
      memset(f,,sizeof(f));
      dfs(,);
      ans=-INF;
      //for(int i=1;i<=n;i++)printf("%lld %lld/%lld %lld:%d %d %lld %lld\n",mx[i][0],mx[i][1],mn[i][0],mn[i][1],mxbh[i],mnbh[i],f[i][0],f[i][1]);
      dfs2(,);
      //ans=-INF;
      //for(int i=1;i<=n;i++)ans=max(ans,f[i][1]);
      //for(int i=1;i<=n;i++)printf("%lld %lld:%d %d\n",f[i][0],f[i][1],mxbh[i],mnbh[i]);
      printf("%lld\n",ans);
    }
    return ;
}

心得：典型的树形DP的题目，换根时的操作还需要更多练习熟练