poj2018 Best Cow Fences[二分答案or凸包优化]

题目。

---

首先暴力很好搞，但是优化的话就不会了。放弃QWQ。

做法1：二分答案

然后发现平均值是$ave=\frac{sum}{len}$，这种形式似乎可以二分答案？把$len$移到左边。

于是二分$ave$，去找数列有没有区间和大于等于其$len$乘以$ave$的，然后卡住了。。

有一个很巧的转化，把每个数都减去一个$ave$，然后任意区间和就相当于把$ave$累加了$len$次。

于是乎只要看区间和$S-len*ave$是否大于等于0就可以了。

存在这样一个区间就说明$ave$可以更大，否则要小。查找存在性是一个简单的前缀和dp。

$O(nlogn)$。

poj精度死活卡不过去。

看来技巧还不够。

于是一气之下把所有double型全换成long long，也就是把小数点后五位通通看成整数，然后运算，最后除以100。

唉。

启示：关于平均数的题目很多时候都是用二分答案处理的。因为是分数形式。

 #include<iostream>
 #include<cstdio>
 #include<cstring>
 #include<algorithm>
 #include<cmath>
 #define dbg(x) cerr << #x << " = " << x <<endl
 using namespace std;
 typedef long long ll;
 typedef double db;
 typedef pair<int,int> pii;
 template<typename T>inline T _min(T A,T B){return A<B?A:B;}
 template<typename T>inline T _max(T A,T B){return A>B?A:B;}
 template<typename T>inline char MIN(T&A,T B){return A>B?(A=B,):;}
 template<typename T>inline char MAX(T&A,T B){return A<B?(A=B,):;}
 template<typename T>inline void _swap(T&A,T&B){A^=B^=A^=B;}
 template<typename T>inline T read(T&x){
     x=;int f=;char c;while(!isdigit(c=getchar()))if(c=='-')f=;
     while(isdigit(c))x=x*+(c&),c=getchar();return f?x=-x:x;
 }
 const int N=1e5+;
 const db eps=1e-;
 ll A[N],s[N];
 ll L=,R,mid;
 int n,l;
 inline bool check(ll ave){
     for(register int i=;i<l;++i)s[i]=s[i-]+A[i]-ave;
     ll minx=1e16;
     for(register int i=l;i<=n;++i){
         MIN(minx,s[i-l]);s[i]=s[i-]+A[i]-ave;
         if(s[i]-minx>=)return ;
     }
     return ;
 }

 int main(){//freopen("test.in","r",stdin);//freopen("test.out","w",stdout);
     read(n),read(l);
     for(register int i=;i<=n;++i)A[i]=read(A[i])*,MAX(R,A[i]);
     while(L<R){
         mid=L+R+>>;
         if(check(mid))L=mid;
         else R=mid-;
     }
     printf("%lld",(L/));
     return ;
 }

做法2：凸包优化

发现以每个点结尾的平均值$ave_i=\frac{S_i-S_j}{i-j}$　　$0 \leq j \leq m$

于是想到斜率。问题变成：在前面的区间内找一点与$i$号点连线斜率最大。

然后发现上凸的3个点，中间那个没有用，所以维护一个下凸包。

查找的话是需要二分的，二分找下凸包里斜率$k_{i-1}<k_{i}>k_{i+1}$的这个点。

但是，基于这题并不是让求每个点结尾的最大平均数，而是全局的。

所以有这么一个神仙思路优化复杂度：

在查找时不要二分了，从队首开始比较，若$k_{l,i}<k_{l+1,i}$则弹出队首。

一直到找到这个最大斜率点，作为这个$i$的局部答案。

如果之后出现一个点，他和之前弹出过的点的斜率比目前没有弹出的点间的斜率都要大呢？

是有这种情况的。

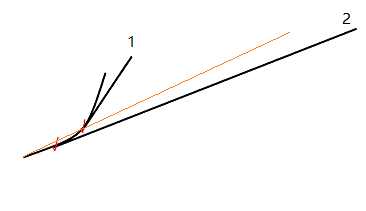
但是，他不会影响全局最优解的形成，即使对于以$i$结尾算错了也没关系。

为什么呢。观察上面这种情况，在1点把下凸包前面一堆全弹掉了。发生这种情况当且仅当这个1号点在橙色线上方。

而2号点那种斜率最大的出现在已经弹出了的点里，必须满足在橙色线下方。

一旦有弹出，那么1号点决策一定比2号点的优。所以2号点算错了也不影响全局最大值。

所以这样的做法是$O(n)$获取全局最优解的。

所以网上说的都是并不严谨的。

这个$O(n)$做法正确性的证明是由hkk神仙提出来的，感谢！大家觉得好可以多去膜他。

 #include<iostream>
 #include<cstdio>
 #include<cstring>
 #include<algorithm>
 #include<cmath>
 #define dbg(x) cerr << #x << " = " << x <<endl
 using namespace std;
 typedef long long ll;
 typedef double db;
 typedef pair<int,int> pii;
 template<typename T>inline T _min(T A,T B){return A<B?A:B;}
 template<typename T>inline T _max(T A,T B){return A>B?A:B;}
 template<typename T>inline char MIN(T&A,T B){return A>B?(A=B,):;}
 template<typename T>inline char MAX(T&A,T B){return A<B?(A=B,):;}
 template<typename T>inline void _swap(T&A,T&B){A^=B^=A^=B;}
 template<typename T>inline T read(T&x){
     x=;int f=;char c;while(!isdigit(c=getchar()))if(c=='-')f=;
     while(isdigit(c))x=x*+(c&),c=getchar();return f?x=-x:x;
 }
 const int N=1e5+;
 db ans;
 int n,m;
 int S[N],q[N],l=,r; 

 int main(){//freopen("test.in","r",stdin);//freopen("test.out","w",stdout);
     read(n),read(m);
     for(register int i=;i<=n;++i)S[i]=S[i-]+read(S[i]);
     for(register int i=m;i<=n;++i){
         while(l<r&&(S[i-m]-S[q[r]])*1ll*(q[r]-q[r-])<=(S[q[r]]-S[q[r-]])*1ll*(i-m-q[r]))--r;
         q[++r]=i-m;
         while(l<r&&(S[i]-S[q[l]])*1ll*(i-q[l+])<=(S[i]-S[q[l+]])*1ll*(i-q[l]))++l;
         MAX(ans,(db)(S[i]-S[q[l]])/(db)(i-q[l]));
     }
     printf("%d\n",(int)(ans*));
     return ;
 }