NOI 2024省选OIFC模拟21 蒲巴巴 超繁做法

题目描述

一年一度的 PuBaBa 杯开始了！

今年的 PuBaBa 杯总共有 \(n\) 个选手来参加，编号分别为 \(1,2,\cdots,n\)，他们的水平按编号依次递增，所以他们过的题目数量单调不降。

作为本场比赛的出题人，PuBaBa 总共出了 \(m\) 道题，他希望第 \(i\) 道题至少有 \(l_i\) 个选手通过，至多有 \(r_i\) 个选手通过，PuBaBa 预计所有题的过题人数和为 \(S\)。

作为毒瘤出题人，PuBaBa 例行会在赛前举行“毒奶”活动。不过，PuBaBa 的毒奶是有依据的，他会计算每位选手最多过的题目数量。

不过，PuBaBa 有点太牛了，他决定将这个简单的任务交给您来完成。

输入格式

第一个，三个正整数 \(n,m,S\) 分别表示参赛选手，题目数量，以及总过题人数。

接下来 \(m\) 行，每行两个正整数 \(l_i,r_i\) 表示第 \(i\) 道题至少有 \(l_i\) 个选手通过，至多有 \(r_i\) 个选手通过。

输出格式

若无解，输出 "-1"（不包含双引号）。

否则，为了压缩输出量，我们令 \(ans_i\) 表示第 \(i\) 个选手的最多过题数。

您仅需输出 \(\bigoplus_{i=1}^{n} ans_ii\)。

样例

Input 1

3 5 8
1 3
2 3
1 3
2 3
1 3

Output 1

5

Input 2

10 8 41
1 7
5 6
5 7
4 9
7 10
1 2
3 10
3 5

Output 2

50

样例解释

对于样例一：\(ans\) 序列为 \(2,4,5\)。

对于样例二：\(ans\) 序列为 \(4,4,5,5,6,7,7,7,8,8\)。

数据范围

由于输入量很大，请使用快速的读入方式。

出题人为您准备了一份 fread 板子：https://www.luogu.com.cn/paste/xc3a5u5w。

测试点编号	\(n,m\le\)	特殊性质
\(1\sim 2\)	\(5\)	无
\(3\)	\(100\)	保证 \(l_i=r_i\)
\(4\sim 5\)	\(100\)	无
\(6\sim8\)	\(1000\)	保证 \(l_i=r_i\)
\(9\sim 10\)	\(1000\)	无
\(11\sim12\)	\(2\times 10^5\)	保证 \(l_i=r_i\)
\(13\sim14\)	\(10^5\)	无
\(15\sim16\)	\(2\times 10^5\)	无
\(17\sim18\)	\(5\times 10^5\)	无
\(19\)	\(2\times10^6\)	无
\(20\)	\(5\times10^6\)	无

对于 \(100\%\) 的数据，保证 \(1\le n,m \le 5\times 10^6\)，\(1\le l_i\le r_i\le n\)，\(1\le S\le nm\)。

比某些做法难，总之比题解简单

先问一个问题：一个长度为 \(n\) 的数组 \(a=\{0\}\)，进行 \(m\) 次操作，每次操作选择若干个互不相同的位置使这些位置加 \(1\)。给你一个数组 \(b\)，问这个数组可否通过上述 \(m\) 次操作得出来。

这题非常简单，我们只需要求出 \(\max_b\)，若 \(\max_b\le m\) 则可以，否则不可以。

---

我们将原问题化为一个二维问题，横方向表示题目，纵方向表示这道题做出的人数，黄色矩形表示 \([l_i,r_i]\)。

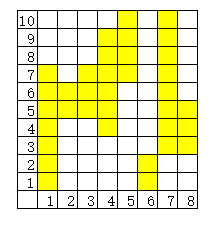
明显得出，我们至少要填 \(\sum l_i\) 个格子，至多能填 \(\sum r_i\) 个格子。如果 \(\sum l_i\le S\le\sum r_i\) 不满足，则答案为 \(-1\)。

我们设考虑到第 \(i\) 个人，则后面有 \(p=n-i+1\) 个人。又设 \(ans_i=j\)。

考虑写一个 check，传入 \(p,j\)，判断是否存在方案。

---

首先，有一个基础的构造，即必须在这个构造上动工。我们设第 \(i\) 个人的做题数为 \(a_i\)。

\[a=\{\underbrace{0,0,\cdots,0}_{n-p个0},\underbrace{j,j,\cdots,j}_{p个j}\}
\]

明显，这是一个满足递增且第 \(i\) 个人为 \(j\) 的方案。它总共填了 \(p\times j\) 个格子。

---

先考虑后面 \(p\) 个人的部分。

我们发现，“做题”的操作就很像上面“加一”的操作——选择若干个互不相同的位置使这些位置加 \(1\)。因为有 \(p\) 个人，所以我们就有 \(p\) 次操作。同理，只有每道题过题人数都小于 \(p\) 才合法。（重申一下，先考虑后面 \(p\) 个人的部分）

也就是说，我们需要画一条粗线，只能取粗线下面的部分。（下面这张图举了 \(p=6\) 的例子）

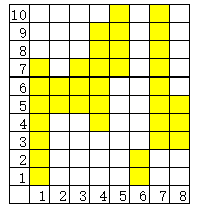
我们发现，对于 \(l_i\le p\)，是合法的，我们可以在后面的部分将其填完，不会超过 \(p\)。至少要填的格子数是 \(\sum l_i[l_i\le p]\)。

但对于 \(l_i>p\)​​，我们只能填 \(p\)​​ 个。只能填的格子数是 \(\sum p[l_i>p]\)​​。

我们可以发现，因为存在 \(l_i>p\)，只能填 \(p\) 个的情况。我们需要在前面 \(n-p\) 个人补全这 \(\sum (l_i-p)[l_i>p]\) 个格子，那么现在每个题都满足下边界 \(l_i\) 了。

那么前面的 \(n-p\) 个人有没有足够的位置补全呢？

答案是有的！

设 \(x=\sum [l_i>p]\)，说明 \(a_{n-p+1}\) 至少为 \(x\)，最多有 \((n-p)x\) 个格子需要补全。

前面的 \(a_i\) 必须小于等于 \(x\)，那么最多有 \((n-p)x\) 个位置，恰好可以补全！

---

我们发现，题目要求我们填恰好 \(S\) 个，我们不一定能填够。由于至少填 \(\sum l_i\) 个，我们有 \(S-\sum l_i\) 个“自由”的格子。

考虑将这些填给后面 \(l_i\le p\) 的题目，努力补全让它们尽量等于 \(p\)。那么总共有 \((S-\sum l_i)+(\sum l_i[l_i\le p])+(\sum p[l_i>p])\) 个格子。将其与至少的格子数 \(pj\) 做比较即可。

---

完了吗？当然没有。我们是不是忘了某个叫 \(r\) 的东西？

因为我们刚刚进行补全，有可能会补到 \(r\) 之外。我们要与至多的进行比较。

我们求出至多的格子数，同上为：\((\sum r_i[r_i\le p])+(\sum p[r_i>p])\)，与刚刚的总共值取 \(\min\)。

也就是得到了 check 函数。

\[\min((S-\sum l_i)+(\sum l_i[l_i\le p])+(\sum p[l_i>p]),(\sum r_i[r_i\le p])+(\sum p[r_i>p]))\ge pj
\]

---

然后发现答案肯定是递增的。

所以可以均摊线性得到答案。

#include <cstdio>
#include <algorithm>
#include <cctype>
using namespace std;
#define ll long long
#define N 5000010
ll n, m, s, mx, mn, ans[N], ANS;
ll l[N], r[N], sl[N], sr[N], cl[N], cr[N];
int main() {
//	freopen("pubaba.in", "r", stdin);
//	freopen("pubaba.out", "w", stdout);
	scanf("%lld %lld %lld", &n, &m, &s);

	for(ll i = 1; i <= m; i++) {
		scanf("%lld %lld", &l[i], &r[i]);
		mn += l[i], mx += r[i];
		sl[l[i]] += l[i];
		sr[r[i]] += r[i];
		cl[l[i]] ++;
		cr[r[i]] ++;
	}
	if(mn > s || mx < s) return printf("-1"), 0;
	for(ll i = 1; i <= n; i++) {
		sl[i] += sl[i-1];
		sr[i] += sr[i-1];
	}
	for(ll i = n; i >= 1; i--) {
		cl[i] += cl[i+1];
		cr[i] += cr[i+1];
	}
	ll pos = n;
	for(ll i = 1; i <= m; i++) {
		while(min(s - mn + sl[pos - 1] + pos * cl[pos], sr[pos - 1] + pos * cr[pos]) < pos * i)
			pos--;
		ans[n - pos + 1] = i;
	}
	for(ll i = 1; i <= n; i++) {
		ans[i] = max(ans[i-1], ans[i]);
		ANS ^= ans[i] * i;
	}
	printf("%lld", ANS);
}