深度学习基础课：使用交叉熵损失函数和Softmax激活函数（下）

大家好~本课程为“深度学习基础班”的线上课程，带领同学从0开始学习全连接和卷积神经网络，进行数学推导，并且实现可以运行的Demo程序

线上课程资料：

本节课录像回放

加QQ群，获得ppt等资料，与群主交流讨论：106047770

本系列文章为线上课程的复盘，每上完一节课就会同步发布对应的文章

本课程系列文章可进入索引查看：

深度学习基础课系列文章索引

目录

• 主问题：如何加快多分类的训练速度？
  • 结学
• 任务：识别手写数字使用交叉熵损失函数和softmax激活函数
• 任务：改进代码
• 总结
• 参考资料
• 谢谢你~

主问题：如何加快多分类的训练速度？

• “识别手写数字“属于单分类还是多分类？
  
  答：多分类
• “识别手写数字“是否能使用单分类中的交叉熵损失函数？
  
  答：不能
• 为什么？
  
  答：

\[\begin{aligned}
\frac{dE}{dw_{kj}} &=\delta_k a_j \\
&= \frac{dE}{dy_k}\frac{df(net_k)}{dnet_k} a_j \\
\end{aligned}
\]

因为目前的交叉熵损失函数是在单分类下推导的。

而在多分类下，由于原有的激活函数不再适合，需要更换新的激活函数，导致上面公式中的\(\frac{df(net_k)}{dnet_k}\)发生了变化，导致损失函数E也需要改变，

所以需要新的损失函数

• 输出层原来的sigmoid激活函数是否适用于多分类的情况？
  
  答：不适用
• 输出层需要新的激活函数
• 如何设计新的激活函数？
  • 我们现在用a表示激活函数的输出值
  • 激活函数要满足什么条件？
    
    答： \(
    a_k \in [0.0, 1.0] 以及 \sum_{k=1}^n a_k= 1
    \)
  • 你能设计一个满足该条件的激活函数吗？
    
    答：\(a_k = \frac{t_k}{\sum_{i} t_i} 且t_i(包括t_k) >0.0\)
• 我们使用softmax激活函数，它的公式为：
  
  答： \(
  a_k = \frac{e^{net_k}}{\sum_{i=1}^n e^{net_i}}
  \)
  
  为什么\(t_k\)使用\(e^k\)这种函数呢？这可能是因为它大于0.0；并且由于是非线性的所以值的间隔拉的比较开，从而能适应更多的变化
• softmax是否满足条件？
  
  答：满足
• 我们现在用y表示真实值（即标签）
• 如何计算loss？
  
  答：\(
  \overrightarrow{loss} = \overrightarrow{a_{输出层}} - \overrightarrow{y}
  \)
• 如何参考设计单分类误差项公式的思路来设计多分类误差项的公式，使其满足loss与误差项成正比？
  
  答：\(
  \overrightarrow{\delta_{输出层}} =\overrightarrow{loss} = \overrightarrow{a_{输出层}} - \overrightarrow{y}
  \)
• 我们需要将单分类的交叉熵损失函数修改一下，使其满足什么公式？
  
  答：为了简单，我们暂时不考虑误差项向量，而只考虑单个神经元的误差项。所以应该满足下面的公式：
  
  \(
  E = ?从而
  \sum_{i=1}^n \frac{dE}{da_i} \frac{da_i}{dnet_k}=\delta_k =a_k - y_k
  \)
  
  （注意：因为每个a的计算都有所有的net参加，所以要使用全导数公式进行累加）
• 现在直接给出修改后的交叉熵损失函数的公式： \(E = - \sum_{j=1}^n y_j \ln a_j \\\)
• 请根据修改后的损失函数和softmax激活函数公式，推导误差项，看下是否为设计的公式： \(
  \delta_k =\sum_{i=1}^n \frac{dE}{da_i} \frac{da_i}{dnet_k}= ?(应该为a_k - y_k)
  \)

答：

\(\because\)

\[\begin{aligned}

\frac{dE}{da_i} &= \frac{d- \sum_{j=1}^n y_j \ln a_j }{da_i}
&= - \frac{y_i}{a_i}

\end{aligned}
\]

\(\therefore\)

\[\begin{aligned}

\delta_k &= \sum_{i=1}^n \frac{dE}{da_i} \frac{da_i}{dnet_k} \\
&= - \sum_{i=1}^n \frac{y_i}{a_i} \frac{da_i}{dnet_k} \\

\end{aligned}
\]

因为只能有一个真实值为1，所以假设\(y_j=1\)，其它\(y_i=0\)，则

\[\begin{aligned}

\delta_k &= - \frac{1}{a_j} \frac{da_j}{dnet_k} \\

\end{aligned}
\]

现在需要推导\(\frac{da_j}{dnet_k}\)，推导过程如下：

因为\(a_j\)可以看作是\(net_j\)的复合函数：

\[
a_j =\frac{e^{net_j}}{\sum_{m=1}^n e^{net_m}} = f(e^{net_j}, \sum_m e^{net_m})

\\

\]

所以：

\[\frac{da_j}{dnet_k} = \frac{da_j}{de^{net_k}} \frac{de^{net_k}}{dnet_k} + \frac{da_j}{d\sum_m e^{net_m}} \frac{d\sum_m e^{net_m}}{dnet_k} \\

\]

现在分两种情况：

• 若 k = j

\[\frac{da_j}{dnet_k} =
\frac{da_j}{dnet_j}
=
\frac{da_j}{de^{net_j}} \frac{de^{net_j}}{dnet_j} + \frac{da_j}{d\sum_m e^{net_m}} \frac{d\sum_m e^{net_m}}{dnet_j} \\
\]

\(\because\)

\[

\begin{aligned}

\frac{da_j}{de^{net_j}} &= \frac{1}{\sum_j e^{net_j}} \\

\frac{de^{net_j}}{dnet_j} &= e^{net_j}\\

\frac{da_j}{d\sum_m e^{net_m}} &= - \frac{e^{net_j}}{(\sum_m e^{net_m})^2} \\

\frac{d\sum_m e^{net_m}}{dnet_k} &= \frac{d\sum_m e^{net_m}}{de^{net_k}} \frac{de^{net_k}}{dnet_k}
= e^{net_k} \\

\end{aligned}
\]

\(\therefore\)

\[

\frac{da_j}{dnet_k} =
\frac{da_j}{dnet_j}
= a_j(1-a_j)
\]

• 若 k \(\neq\) j

\[\frac{da_j}{dnet_k} = \frac{da_j}{de^{net_k}} \frac{de^{net_k}}{dnet_k} + \frac{da_j}{d\sum_m e^{net_m}} \frac{d\sum_m e^{net_m}}{dnet_k} \\
\]

\(\because\)

\[

\begin{aligned}

\frac{da_j}{de^{net_k}} &= 0 \\

\frac{da_j}{d\sum_m e^{net_m}} &= - \frac{e^{net_j}}{(\sum_m e^{net_m})^2} \\

\frac{d\sum_m e^{net_m}}{dnet_k} &= e^{net_k} \\

\end{aligned}
\]

\(\therefore\)

\[

\frac{da_j}{dnet_k}
= -a_j a_k
\]

经过上面的推导后，写成向量的形式就是：

\[
\overrightarrow{\delta_{输出层}} = \begin{bmatrix}
- \frac{1}{a_j} \cdot (-a_j a_1) \\
\vdots \\
- \frac{1}{a_j} \cdot (a_j(1-a_j)) \\
\vdots \\
- \frac{1}{a_j} \cdot (-a_j a_n) \\
\end{bmatrix}

= \begin{bmatrix}
a_1 \\
\vdots \\
a_j - 1 \\
\vdots \\
a_n \\
\end{bmatrix}

= \overrightarrow{a_{输出层}} - \overrightarrow{y} \\

\]

结学

• 如何加快多分类的训练速度？
• 根据交叉熵损失函数和softmax，推导误差项的过程是什么？

任务：识别手写数字使用交叉熵损失函数和softmax激活函数

• 请在“识别手写数字Demo”中使用交叉熵损失函数和softmax激活函数，并且加入“通过打印loss来判断收敛”
  
  答：待实现的代码为：NewCross_softmax，实现后的代码为：NewCross_softmax_answer
• 请每个同学运行代码
  • 刚开始训练时，有什么警告？
    
    答：如下图所示：有“输出层梯度过大”的警告
    
    
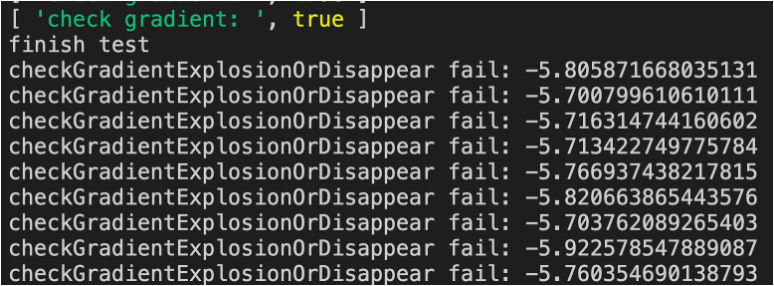
  • 注释掉警告代码后，看下loss的训练速度与之前的代码相比是否明显加快？
    
    答：没有

任务：改进代码

• 找到发生警告的原因？
  
  答：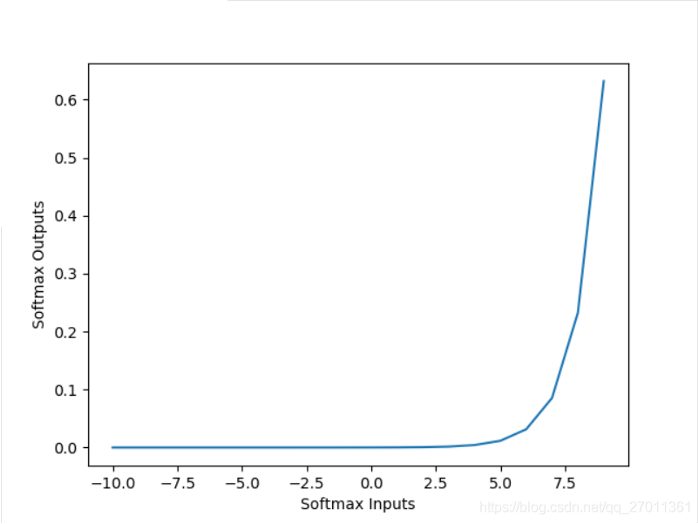
  
  因为输出层加权和没有做缩小处理，所以加权和比较大（范围为[10.0,15.0]左右）。
  
  通过上图(softmax的图像)可知，该范围内的梯度很大，所以报“梯度爆炸”的警告
• 如何改进代码？
  
  答：将输出层的学习率变小为0.1
• 将输出层的学习率分别变小为1.0、0.1，运行代码，看是否解决了警告，并提升了训练速度？
  
  答：变小为0.1后运行代码的结果如下图所示：
  
  
  
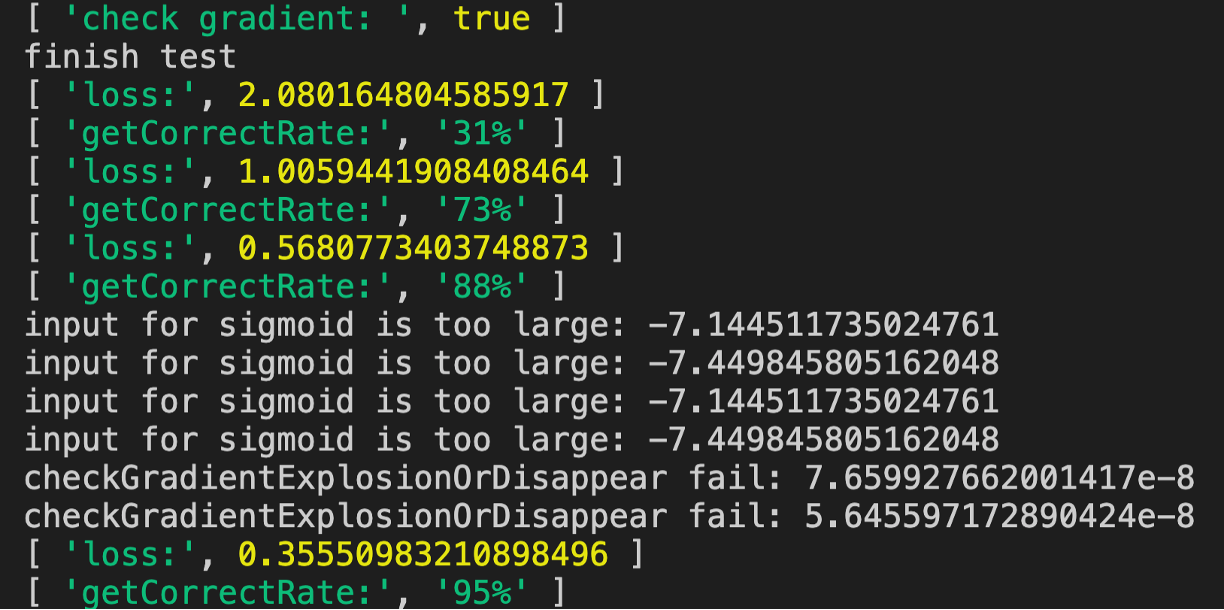
  我们看到只需要四轮训练既达到95%的正确率
  
  那么为什么在正确率到88%后会开始报输出层的一些梯度值过小的警告呢？这是因为此时loss小，所以梯度也小了

总结

• 请总结本节课的内容？
• 请回答所有主问题？

参考资料

• Improving the way neural networks learn
• 超详细的softmax的反向传播梯度计算推导
• Softmax与交叉熵损失的实现及求导

谢谢你~