吴恩达优化算法 (Optimization algorithms)笔记

Mini-batch 梯度下降（Mini-batch gradient descent）

使用batch梯度下降法，一次遍历训练集只能让你做一个梯度下降，使用mini-batch梯度下降法，一次遍历训练集，能让你做样本数/每组个数个梯度下降。



使用batch梯度下降法时，每次迭代你都需要历遍整个训练集，可以预期每次迭代成本都会下降，所以如果成本函数\(j\)是迭代次数的一个函数，它应该会随着每次迭代而减少，如果\(j\)在某次迭代中增加了，那肯定出了问题，也许你的学习率太大。

使用mini-batch梯度下降法，如果你作出成本函数在整个过程中的图，则并不是每次迭代都是下降的，特别是在每次迭代中



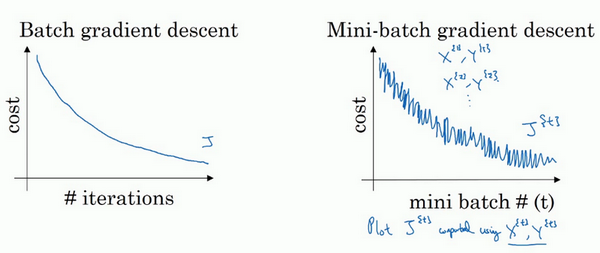
需要决定的变量之一是mini-batch的大小，mini-batch=1就是随机梯度下降(SGD),batch拉满就是批量(全量)梯度下降(BGD)。所以Mini-Batch是批量梯度和随机梯度的一种折中方案。在精度和速度上都做了一些取舍。因为如果使用随机梯度下降法，如果你只要处理一个样本，那这个方法很好，这样做没有问题，通过减小学习率，噪声会被改善或有所减小，但随机梯度下降法的一大缺点是，你会失去所有向量化带给你的加速，因为一次性只处理了一个训练样本，这样效率过于低下，所以实践中最好选择不大不小的mini-batch尺寸，实际上学习率达到最快。你会发现两个好处，一方面，你得到了大量向量化，上个视频中我们用过的例子中，如果mini-batch大小为1000个样本，你就可以对1000个样本向量化，比你一次性处理多个样本快得多。另一方面，你不需要等待整个训练集被处理完就可以开始进行后续工作，再用一下上个视频的数字，每次训练集允许我们采取5000个梯度下降步骤，所以实际上一些位于中间的mini-batch大小效果最好。



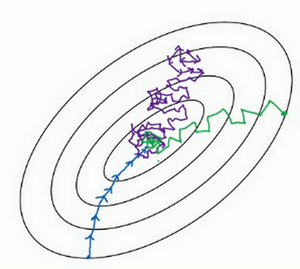
用mini-batch梯度下降法，我们从这里开始，一次迭代这样做，两次，三次，四次，它不会总朝向最小值靠近，但它比随机梯度下降要更持续地靠近最小值的方向，它也不一定在很小的范围内收敛或者波动，如果出现这个问题，可以慢慢减少学习率。

考虑到电脑内存设置和使用的方式，如果mini-batch大小是2的\(n\)次方

指数加权平均数（Exponentially weighted averages）

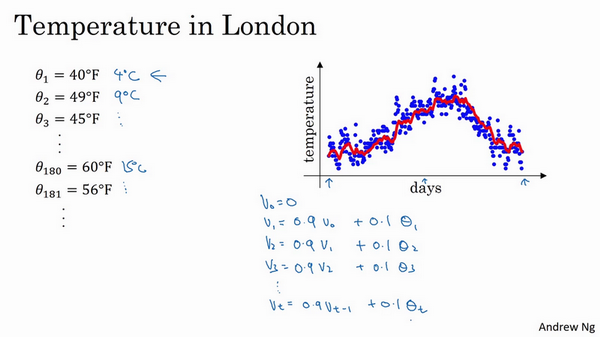
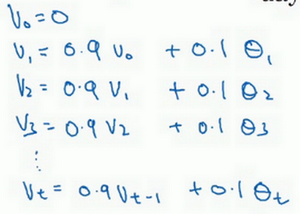
你要做的是，首先使\(v_{0}=0\)，每天，需要使用0.9的加权数之前的数值加上当日温度的0.1倍，即\(v_{1}=0.9v_{0}+0.1\Theta_{1}\)，(\(\Theta_{1}\)当天温度)所以这里是第一天的温度值。

第二天，又可以获得一个加权平均数，0.9乘以之前的值加上当日的温度0.1倍，即\(v_{2}=0.9v_{1}+0.1\Theta_{2}\)，以此类推。

第二天值加上第三日数据的0.1，如此往下。大体公式就是某天的等于前一天值的0.9加上当日温度的0.1。

如此计算，然后用红线作图的话，便得到这样的结果。



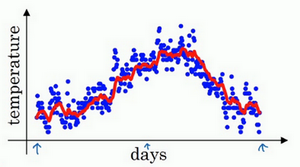
通常\(v_{t}=0.9v_{t-1}+0.1\Theta_{t}\)里面的0.9这个常数变成\(\beta\),0.1则是\((1-\beta)\)。即\(v_{t}=\beta v_{t-1}+(1-\beta)\Theta_{t}\)

\(\beta=0.9\)的时候，得到的结果是红线，如果它更接近于1，比如0.98，结果就是绿线，如果\(\beta\)小一点，如果是0.5，结果就是黄线。



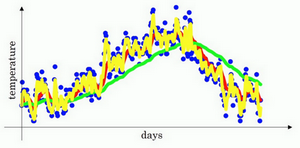
我们进一步地分析，来理解如何计算出每日温度的平均值。

同样的公式，\(v_{t}=\beta v_{t-1}+(1-\beta)\Theta_{t}\)

使\(\beta=0.9\)，写下相应的几个公式，所以在执行的时候，\(t\)从0到1到2到3，\(t\)的值在不断增加，为了更好地分析，我写的时候使得\(t\)的值不断减小，然后继续往下写。





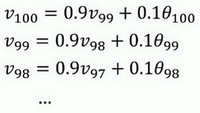
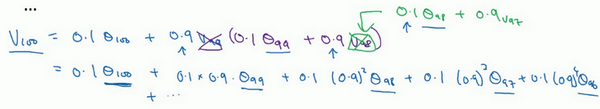
到底需要平均多少天的温度。\((0.9)^{10}\)实际上大约为0.35，这大约是\(\frac{1}{e}\)，e是自然算法的基础之一。大体上说，如果有\(1-\varepsilon\)，在这个例子中，\(\varepsilon=0.1\)，所以\(1-\varepsilon=0.9\)，\((1-\varepsilon)^{\frac{1}{\varepsilon}}\)约等于\(\frac{1}{e}\)，大约是0.34，0.35，换句话说，10天后，曲线的高度下降到\(\frac{1}{3}\)，相当于在峰值的\(\frac{1}{e}\)。

又因此当\(\beta=0.9\)的时候，我们说仿佛你在计算一个指数加权平均数，只关注了过去10天的温度，因为10天后，权重下降到不到当日权重的三分之一。

指数加权平均的偏差修正（Bias correction in exponentially weighted averages）

\(v_{t}=\beta v_{t-1}+(1-\beta)\Theta_{t}\)

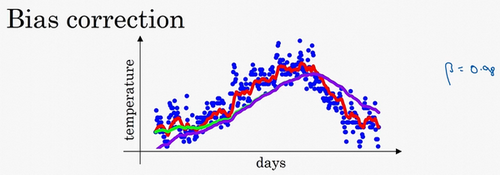
这个（红色）曲线对应的\(\beta\)值为0.9，这个（绿色）曲线对应的\(\beta\)=0.98，如果你执行写在这里的公式，在\(\beta\)等于0.98的时候，得到的并不是绿色曲线，而是紫色曲线，你可以注意到紫色曲线的起点较低，我们来看看怎么处理。

有个办法可以修改这一估测，让估测变得更好，更准确，特别是在估测初期，也就是不用\(v_{t}\)，而是用\(\frac{v_{t}}{1-\beta^{t}}\)，t就是现在的天数。举个具体例子，当\(t=2\)时，\(1-\beta^{t}=1-0.98^{2}=0.0396\)，因此对第二天温度的估测变成了\(\frac{v_{2}}{0.0396}=\frac{0.0196\Theta_{1}+0.02\Theta_{2}}{0.0396}\)，也就是\(\Theta_{1}\)和\(\Theta_{2}\)的加权平均数，并去除了偏差。你会发现随着\(t\)增加，\(\beta^{t}\)接近于0，所以当\(t\)很大的时候，偏差修正几乎没有作用，因此当\(t\)较大的时候，紫线基本和绿线重合了。不过在开始学习阶段，你才开始预测热身练习，偏差修正可以帮助你更好预测温度，偏差修正可以帮助你使结果从紫线变成绿线。



在机器学习中，在计算指数加权平均数的大部分时候，大家不在乎执行偏差修正，因为大部分人宁愿熬过初始时期，拿到具有偏差的估测，然后继续计算下去。如果你关心初始时期的偏差，在刚开始计算指数加权移动平均数的时候，偏差修正能帮助你在早期获取更好的估测。

动量梯度下降法（Gradient descent with Momentum）

还有一种算法叫做Momentum，或者叫做动量梯度下降法，运行速度几乎总是快于标准的梯度下降算法，简而言之，基本的想法就是计算梯度的指数加权平均数，并利用该梯度更新你的权重，在本视频中，我们呢要一起拆解单句描述，看看你到底如何计算。



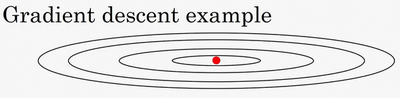
例如，如果你要优化成本函数，函数形状如图，红点代表最小值的位置，假设你从这里（蓝色点）开始梯度下降法，如果进行梯度下降法的一次迭代，无论是batch或mini-batch下降法，也许会指向这里，现在在椭圆的另一边，计算下一步梯度下降，结果或许如此，然后再计算一步，再一步，计算下去，你会发现梯度下降法要很多计算步骤对吧？



慢慢摆动到最小值，这种上下波动减慢了梯度下降法的速度，你就无法使用更大的学习率，如果你要用较大的学习率（紫色箭头），结果可能会偏离函数的范围，为了避免摆动过大，你要用一个较小的学习率。



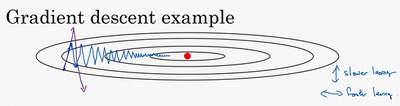
另一个看待问题的角度是，在纵轴上，你希望学习慢一点，因为你不想要这些摆动，但是在横轴上，你希望加快学习，你希望快速从左向右移，移向最小值，移向红点。所以使用动量梯度下降法，你需要做的是，在每次迭代中，确切来说在第\(t\)次迭代的过程中，你会计算微分\(dW\)，\(db\)，我会省略上标\([l]\)，你用现有的mini-batch计算\(dW\)，\(db\)。如果你用batch梯度下降法，现在的mini-batch就是全部的batch，对于batch梯度下降法的效果是一样的。如果现有的mini-batch就是整个训练集，效果也不错，你要做的是计算\(v_{dW}=\beta v_{dW}+(1-\beta)dW\)，这跟我们之前的计算相似，也就是\(v_{t}=\beta v_{t-1}+(1-\beta)\Theta_{t}\)，\(dW\)的移动平均数，接着同样地计算\(v_{db}\)，\(v_{db}=\beta v_{db}+(1-\beta)db\)，然后重新赋值权重，\(W:=W-av_{dw}\)，同样\(b:=b-av_{db}\)，这样就可以减缓梯度下降的幅度。

例如，在上几个导数中，你会发现这些纵轴上的摆动平均值接近于零，所以在纵轴方向，你希望放慢一点，平均过程中，正负数相互抵消，所以平均值接近于零。但在横轴方向，所有的微分都指向横轴方向，因此横轴方向的平均值仍然较大，因此用算法几次迭代后，你发现动量梯度下降法，最终纵轴方向的摆动变小了，横轴方向运动更快，因此你的算法走了一条更加直接的路径，在抵达最小值的路上减少了摆动。

动量梯度下降法的一个本质，这对有些人而不是所有人有效.

最后我们来看具体如何计算，算法在此。



所以你有两个超参数，学习率\(a\)以及参数\(\beta\)，\(\beta\)控制着指数加权平均数。\(\beta\)最常用的值是0.9，我们之前平均了过去十天的温度，所以现在平均了前十次迭代的梯度。实际上\(\beta\)为0.9时，效果不错，你可以尝试不同的值，可以做一些超参数的研究，不过0.9是很棒的鲁棒数。那么关于偏差修正，所以你要拿\(v_{dW}\)和\(v_{db}\)除以\(1-\beta^{t}\)，实际上人们不这么做，因为10次迭代之后，因为你的移动平均已经过了初始阶段。实际中，在使用梯度下降法或动量梯度下降法时，人们不会受到偏差修正的困扰。当然\(v_{dW}\)初始值是0，要注意到这是和\(dW\)拥有相同维数的零矩阵，也就是跟\(W\)拥有相同的维数，\(v_{db}\)的初始值也是向量零，所以和\(db\)拥有相同的维数，也就是和\(b\)是同一维数。

RMSprop

知道了动量（Momentum）可以加快梯度下降，还有一个叫做RMSprop的算法，全称是root mean square prop算法，它也可以加速梯度下降，我们来看看它是如何运作的。



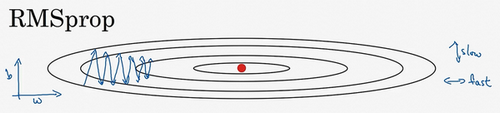
回忆一下我们之前的例子，如果你执行梯度下降，虽然横轴方向正在推进，但纵轴方向会有大幅度摆动，为了分析这个例子，假设纵轴代表参数\(b\)，横轴代表参数\(W\)，可能有\(W1\)，\(W2\)或者其它重要的参数，为了便于理解，被称为\(b\)和\(W\)。

所以，你想减缓\(b\)方向的学习，即纵轴方向，同时加快，至少不是减缓横轴方向的学习，RMSprop算法可以实现这一点。



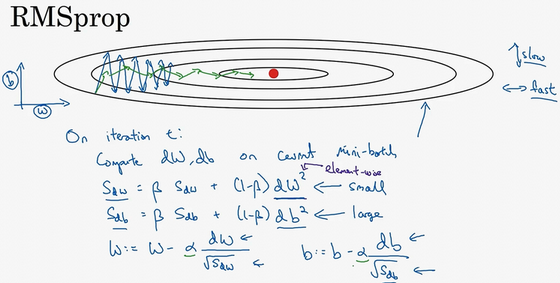
在第次迭代中，该算法会照常计算当下mini-batch的微分\(dW\)，\(db\)，所以我会保留这个指数加权平均数，我们用到新符号\(S_{dW}\)，而不是\(v_{dW}\)，因此\(S_{dW}=\beta S_{dW}+(1-\beta)dW^{2}\)，澄清一下，这个平方的操作是针对这一整个符号的，这样做能够保留微分平方的加权平均数，同样\(S_{db}=\beta S_{db}+(1-\beta)db^{2}\)，再说一次，平方是针对整个符号的操作。

接着RMSprop会这样更新参数值，\(W:=W-a \frac{dW}{\sqrt{S_{dW}}}\)，\(b:=b-a \frac{db}{\sqrt{S_{db}}}\)，我们来理解一下其原理。记得在横轴方向或者在例子中的\(W\)方向，我们希望学习速度快，而在垂直方向，也就是例子中的方向，我们希望减缓纵轴上的摆动，所以有了\(S_{dW}\)和\(S_{db}\)，我们希望\(S_{dW}\)会相对较小，所以我们要除以一个较小的数，而希望\(S_{db}\)又较大，所以这里我们要除以较大的数字，这样就可以减缓纵轴上的变化。你看这些微分，垂直方向的要比水平方向的大得多，所以斜率在\(b\)方向特别大，所以这些微分中，\(db\)较大，\(dW\)较小，因为函数的倾斜程度，在纵轴上，也就是b方向上要大于在横轴上，也就是\(W\)方向上。\(db\)的平方较大，所以\(S_{db}\)也会较大，而相比之下，\(dW\)会小一些，亦或\(dW\)平方会小一些，因此\(S_{dW}\)会小一些，结果就是纵轴上的更新要被一个较大的数相除，就能消除摆动，而水平方向的更新则被较小的数相除。



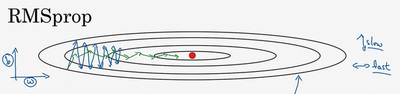
RMSprop的影响就是你的更新最后会变成这样（绿色线），纵轴方向上摆动较小，而横轴方向继续推进。还有个影响就是，你可以用一个更大学习率\(a\)，然后加快学习，而无须在纵轴上垂直方向偏离。

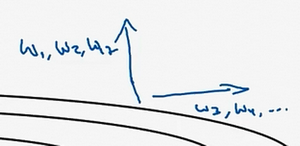
要说明一点，我一直把纵轴和横轴方向分别称为\(b\)和\(W\)，只是为了方便展示而已。实际中，你会处于参数的高维度空间，所以需要消除摆动的垂直维度，你需要消除摆动，实际上是参数\(W_{1}\)，\(W_{2}\)等的合集，水平维度可能\(W_{3}\)，\(W_{4}\)等等，因此把\(W\)和\(b\)分开只是方便说明。实际中\(dW\)是一个高维度的参数向量，\(db\)也是一个高维度参数向量，但是你的直觉是，在你要消除摆动的维度中，最终你要计算一个更大的和值，这个平方和微分的加权平均值，所以你最后去掉了那些有摆动的方向。所以这就是RMSprop，全称是均方根，因为你将微分进行平方，然后最后使用平方根。



如果\(S_{dW}\)的平方根趋近于0怎么办？得到的答案就非常大，为了确保数值稳定，在实际操练的时候，你要在分母上加上一个很小很小的\(\varepsilon\)，\(\varepsilon\)是多少没关系，\(10^{-8}\)是个不错的选择(python:\(1e-8\))，这只是保证数值能稳定一些，无论什么原因，你都不会除以一个很小很小的数。

Adam 优化算法(Adam optimization algorithm)

在深度学习的历史上，包括许多知名研究者在内，提出了优化算法，并很好地解决了一些问题，但随后这些优化算法被指出并不能一般化，并不适用于多种神经网络，时间久了，深度学习圈子里的人开始多少有些质疑全新的优化算法，很多人都觉得动量（Momentum）梯度下降法很好用，很难再想出更好的优化算法。所以RMSprop以及Adam优化算法（Adam优化算法也是本视频的内容），就是少有的经受住人们考验的两种算法，已被证明适用于不同的深度学习结构，这个算法我会毫不犹豫地推荐给你，因为很多人都试过，并且用它很好地解决了许多问题。

Adam优化算法基本上就是将Momentum和RMSprop结合在一起，那么来看看如何使用Adam算法。



所以Adam算法结合了Momentum和RMSprop梯度下降法(缝合怪！！)，并且是一种极其常用的学习算法，被证明能有效适用于不同神经网络，适用于广泛的结构。



本算法中有很多超参数，超参数学习率\(a\)很重要，也经常需要调试，你可以尝试一系列值，然后看哪个有效。\(\beta_{1}\)常用的缺省值为0.9，这是\(dW\)的移动平均数，也就是\(dW\)的加权平均数，这是Momentum涉及的项。至于超参数\(\beta_{2}\)，Adam论文作者，也就是Adam算法的发明者，推荐使用0.999，这是在计算\((dW)^2\)以及\((db)^2\)的移动加权平均值，关于\(\varepsilon\)的选择其实没那么重要，Adam论文的作者建议\(\varepsilon\)为\(10^{-8}\)，但你并不需要设置它，因为它并不会影响算法表现。但是在使用Adam的时候，人们往往使用缺省值即可，\(\beta_{1}\)，\(\beta_{2}\)和\(\varepsilon\)都是如此，我觉得没人会去调整\(\varepsilon\)，然后尝试不同的\(a\)值，看看哪个效果最好。你也可以调整\(\beta_{1}\)和\(\beta_{2}\)，但我认识的业内人士很少这么干。

为什么这个算法叫做Adam？Adam代表的是Adaptive Moment Estimation，\(\beta_{1}\)用于计算这个微分（\(dW\)），叫做第一矩，\(\beta_{2}\)用来计算平方数的指数加权平均数（\((dW)^{2}\)），叫做第二矩，所以Adam的名字由此而来，但是大家都简称Adam权威算法。