【LeetCode栈与队列#05】滑动窗口最大值

滑动窗口最大值

力扣题目链接(opens new window)

给定一个数组 nums，有一个大小为 k 的滑动窗口从数组的最左侧移动到数组的最右侧。你只可以看到在滑动窗口内的 k 个数字。滑动窗口每次只向右移动一位。

返回滑动窗口中的最大值。

进阶：

你能在线性时间复杂度内解决此题吗？

提示：

• 1 <= nums.length <= 10^5
• -10^4 <= nums[i] <= 10^4
• 1 <= k <= nums.length

思路

虽然本题在LeetCode上为困难级别，但是似乎很容易想到对应的暴力解法，首先我们得明白这题难在哪里

使用暴力解法

本题的难点在于使用一般的方法解，时间复杂度会很高

一种很自然的想法是：滑动窗口遍历过程中，我们又去遍历窗口内的数，比较大小后返回最大值

那么这种方法的时间复杂度为O(n*k)，k为窗口大小，n为数组遍历次数

使用队列行不行？

观察滑动窗口移动的方式，和队列有点像

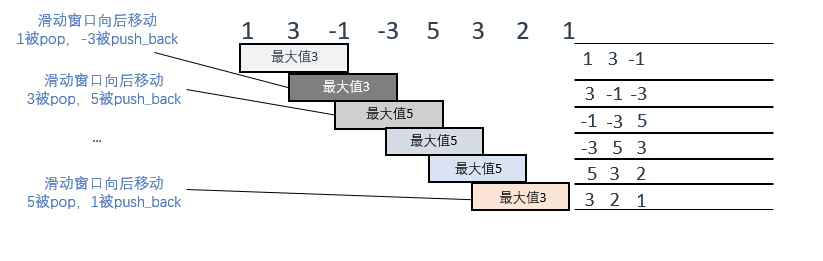
使用队列模拟滑动窗口，窗口每次向右移动一个单位，只需将队列的首位pop并将下一个数添加到队尾即可完成操作

那么可不可以用优先级队列来获取窗口内的最大值呢？

可以，但是会破坏窗口内元素的顺序，不利于后续操作

例如，当前窗口内的数为{1,3,-1}

如果将其放入优先级队列，那么顺序就会变为{3,1,-1}

很好，找到最大值3了。但是窗口向后移动时，按原来的设想，我们需要把1弹出，但是现在1被夹在中间，pop不了，出现问题。所以不能用优先级队列去做

自定义队列

逻辑

虽然不能用优先级队列去解决本题，但是这个思考过程是可以借鉴的

这里需要明确一点：队列中的元素顺序其实并不重要，队列只是用于模拟滑动窗口的一个数据结构

队列中数据的进出只需要满足滑动窗口移动的规则即可

因此，我们可以设想这样一种自定义队列：

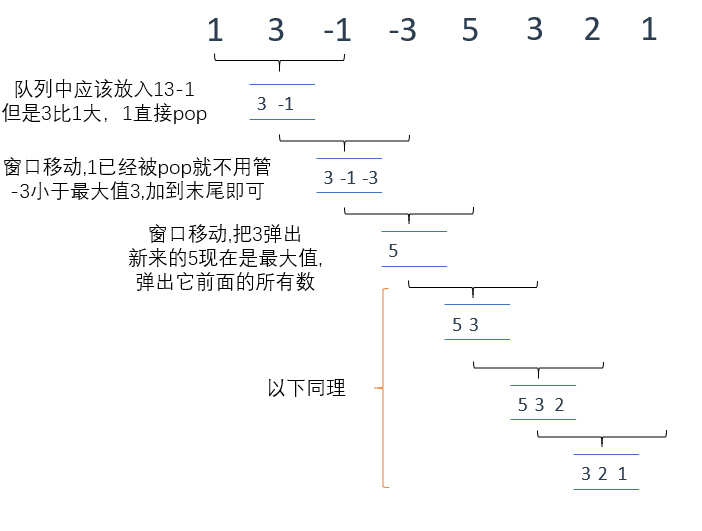
该队列的队头永远是当前滑动窗口中的最大值，当滑动窗口移动时，我们就把新的数添加到队尾。

如果新数比队头的数还要大，那么将之前所有的队内元素弹出，使新数位于队头，如此循环

这种队列被称为单调队列

然后我们再通过一个函数去获取队列首部的最大值就可以实现题目的要求了，最终结果是{3,3,5,5,5,3}

总结一下，我们需要实现的队列结构大致如下：

class MyQueue {
public:
    void pop(int value) {
    }
    void push(int value) {
    }
    int front() {
        return que.front();
    }
};

实现

那么想法有了，用什么数据结构去实现这个单调队列呢？--> deque

实现单调队列MyQueue

如上面说的，单调队列类MyQueue中提供pop、push、front三个方法

pop

用于弹出元素

每次弹出之前要先判断当前队列是否为空，以及输入值是否与队头数据相等

void pop(int value){
    if(!que.empty() && value == que.front()){
        que.pop_front();//弹出队首元素
    }
}

如果要pop的元素是队首元素，说明当前最大值需要更新，并且该更新是因为窗口移动导致的，而不是来了个新的最大值

简单来说，不是每次滑动窗口移动都需要调用pop，pop函数只负责单纯的pop掉队列开头的元素

如果有新的数值进来并且是最大值，那么将新的最大值移动到队首的操作会由push函数实现

push

用于将新元素添加到队尾

void push(int value){
    while(!que.empty() && value > que.back()){//如果新元素一直大于队尾的数，就不断将队尾数pop
        que.pop_back();
    }
    //直到遇到比新元素更大的值或者只剩下新元素
    que.push_back(value);
}

front

用于查询队列头部的元素

		// 查询当前队列里的最大值 直接返回队列前端也就是front就可以了。
        int front() {
            return que.front();
        }

完整代码

class MyQueue {
public:
    deque<int> que;
    void pop(int value) {
        if(!que.empty() && value == que.front()){
        	que.pop_front();//弹出队首元素
    	}
    }
    void push(int value) {
        while(!que.empty() && value > que.back()){//如果新元素一直大于队尾的数，就不断将队尾数pop
        	que.pop_back();
    	}
    	//直到遇到比新元素更大的值或者只剩下新元素
    	que.push_back(value);
    }
    int front() {
        return que.front();
    }
};

整体代码

步骤：

1、使用deque实现单调队列MyQueue

2、实例化单调队列

3、将整数数组中k（窗口大小）个元素遍历加入队列中

4、res记录当前k个数中的最大值

5、开始移动窗口遍历整数数组

• 使用pop配合push模拟窗口的滑动
• 记录当前最大值

6、返回结果数组res

class Solution {
private:
    class MyQueue{
        public:

            deque<int> que;
            void pop(int value){
                if(!que.empty() && value == que.front()){
                    que.pop_front();//弹出队首元素
                }
            }

            void push(int value){
                while(!que.empty() && value > que.back()){//如果新元素一直大于队尾的数，就不断将队尾数pop
                    que.pop_back();
                }
                //直到遇到比新元素更大的值或者只剩下新元素
                que.push_back(value);//注意用的是自己实现的push，不是push_back
            }

            int front(){// 查询当前队列里的最大值 直接返回队列前端也就是front就可以了。
                return que.front();
            }
    };

public:
    vector<int> maxSlidingWindow(vector<int>& nums, int k) {
        MyQueue que;
        //输出值是数组
        vector<int> res;
        //将滑动窗口初始位置的值加入
        for(int i = 0; i < k; ++i){
            que.push(nums[i]);
        }//此时执行完后，que中为[3,-1]
        //记录当前最大值
        res.push_back(que.front());//初始窗口中也要取最大值，不然会漏情况

        //模拟窗口移动
        for(int i = k; i < nums.size(); ++i){//注意从k开始
            que.pop(nums[i - k]);//将窗口最前面的数pop掉
            que.push(nums[i]);//往窗口末尾加入新数，使窗口向右移动
            res.push_back(que.front());//记录当前窗口的最大值
        }
        return res;
    }
};

主函数部分说明

主函数逻辑：

1、实例化MyQueue、结果数组vector res；

2、初始化滑动窗口，即先使用自定义的push(不是push_back)把数组前k个数放入队列（同时就排好序了）

3、将当前初始化窗口的最大值保存（用vector提供的方法：push_back）

4、模拟窗口移动（注意遍历开始的位置，以及窗口头部和尾部位置）

补充知识

vector添加元素用push_back，deuqe也用这个

TBD

二刷问题

1、自定义的队列类MyQueue记得写作用域public

2、在主代码中维护的que队列不是所谓的"窗口"，它只是用来保证我们设想的窗口中最左边的值永远是最大值（队首），可以类比辅助栈的作用

3、一开始我们需要往窗口中填入窗口大小的元素，加入元素的方式是自定义类中的push方法，加完之后也要保存当前队列首部的最大值，不要漏情况

4、遍历是从k开始的，不是0