【LeetCode二叉树#16】二叉(搜索)树的最近公共祖先(递归后序遍历,巩固回溯机制)
二叉树的最近公共祖先
给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。
百度百科中最近公共祖先的定义为:“对于有根树 T 的两个结点 p、q,最近公共祖先表示为一个结点 x,满足 x 是 p、q 的祖先且 x 的深度尽可能大(一个节点也可以是它自己的祖先)。”
例如,给定如下二叉树: root = [3,5,1,6,2,0,8,null,null,7,4]
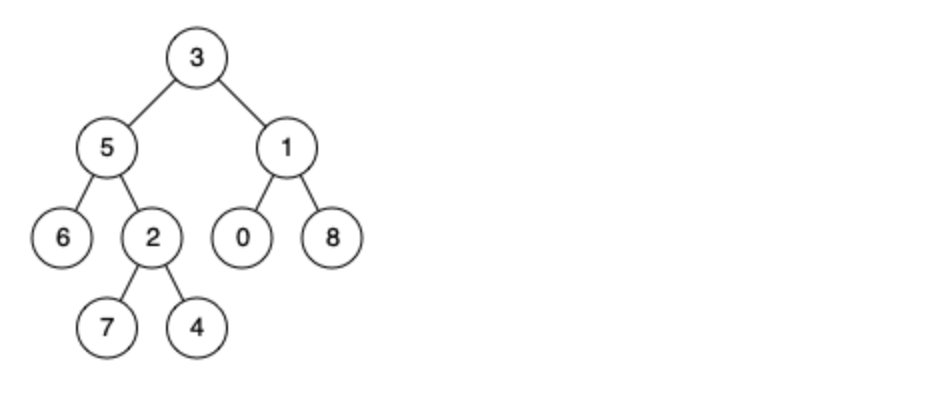
示例 1: 输入: root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 1 输出: 3 解释: 节点 5 和节点 1 的最近公共祖先是节点 3。
示例 2: 输入: root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 4 输出: 5 解释: 节点 5 和节点 4 的最近公共祖先是节点 5。因为根据定义最近公共祖先节点可以为节点本身。
说明:
- 所有节点的值都是唯一的。
- p、q 为不同节点且均存在于给定的二叉树中
思路
根据题目要求,我们需要先找到对应的两个节点p、q,然后再回去找他们的最近的公共父节点
这么一个过程实际上顺序是自下而上的,也就是说,如果能从下往上搜索父节点,那么这个问题就好解决了,如何做到呢?
首先,节点p、q肯定是左右节点,那么我们遍历的时候肯定得先遍历到这两个左右节点
符合上述条件的遍历方式是:后序遍历(左右中)
其次,当找到节点p、q,我们需要"回头"往上找他们的公共父节点,实际上就可以在左右中的 中 里面处理查找公共父节点的逻辑
后序遍历也满足查找父节点的要求
判断公共祖先
遍历方式确定了,那么还需要解决一个问题:怎么判断一个节点是不是节点q和节点p的公共祖先?
这里一共有两种情况:
情况1
最容易想到的是第一种,即当遍历到某个节点A,其左子节点B找到p(并返回),右子节点C找到q(并返回),那么此时可以认为节点A是B、C的最近公共祖先
图示如下:
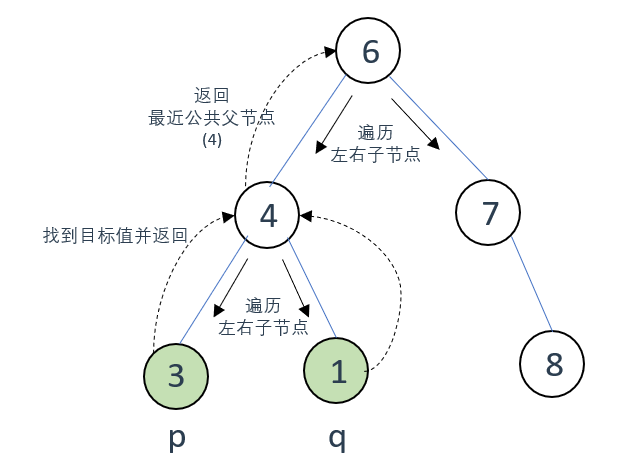
从根节点6开始进行后序遍历,那么先遍历6的左子节点4和右子节点7
(先进入左子节点4的递归中)
到4之后,因为其左右子节点不为空,使用又继续按后序顺序遍历
此时在4的左子节点找到了p,返回
在4的右子节点找到了q,返回
然后再p、q的父节点4这里处理逻辑:找到目标节点,当前根节点4为最近公共节点
于是把4往根节点6传
最后的效果就是:在递归函数中输入了一颗二叉树的根节点6,然后通过递归找到了目标节点p、q,然后通过后序遍历左右中的顺序在 中 里面处理了最近公共父节点的判断逻辑,并把处理所得的最近公共父节点通过回溯传到递归的第一层,得到结果
情况2

还是从根节点6开始,只不过这次我们在6的左子节点就找到了q
因为还没有找到p,并且节点4还有子节点,所以还得继续遍历(只要没有找齐p、q都应该继续遍历,因此在该问题中,我们可能被迫需要遍历整颗二叉树而不是找到目标值就返回)
继续
遍历节点4的左右子节点,在左子节点找到p,并且其没有子节点,此时需要返回
在节点4的位置处理其左右子节点返回的结果,并给出当前p、q的最近公共父节点(具体操作在代码里再解释),实际上就是节点4
于是我们得到了p、q的最近公共父节点,此时将结果往上返回,得出最后的解
总结
通过分析两种情况,可以发现:不论p、q以哪种方式被找到,最终的处理过程都在左右中顺序里面的 中 的位置处理。(也就是调用递归函数时输入的节点。从递归函数的角度讲,该节点为根节点;从我们遍历的角度讲,该节点为当前节点,也就是左右中里面位于 中 的节点)
因此,情况2会被情况1包含,在处理情况1的逻辑下,情况2会被一并处理
代码分析
还是写递归的老一套
1、确定递归函数参数和返回值
首先能够确定的是,这里的递归函数需要返回值,因为我们需要通过返回值来了解是否找到了p、q
一种直接的想法是返回bool值,但是不行
因为在中节点位置完成逻辑处理后,我们需要返回的是 最近公共父节点 ,这是一个节点类型值
所以干脆直接就设定返回值为节点类型,如果有返回值就表明找到p或q
这样的话还可以利用解题模板
class Solution {
public:
TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
}
};
2、确定终止条件
根据上面的分析,递归结束的情况有:
- 当找到p
- 找到q
- 当前输入的节点root为NULL
class Solution {
public:
TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
if(root == p || root ==q || root == NULL) return root;
}
};
如果 root == q,或者 root == p,说明找到 q p ,则将其返回,这个返回值,后面在中节点的处理过程中会用到
3、确定单层处理逻辑
因为本题中需要使用回溯机制来处理返回值,而后序遍历的顺序是 左右中
我们是在中节点位置处理父节点判断逻辑的,但是由于是先遍历 左右 节点
因此在得到返回值并处理之前,需要等待左右节点的递归遍历完成,而递归一旦触发,就会一直遍历下去直到递归函数的输入为NULL,也就是遇到叶子节点才会结束
因此,在本题中,由于使用了后序遍历,我们被迫遍历了整颗二叉树
根据在路径总和问题中的讨论有提到这种情况
题外话
如果递归函数有返回值,如何区分要搜索一条边,还是搜索整个树呢?
搜索一条边的写法:
if (递归函数(root->left)) return ;
if (递归函数(root->right)) return ;
搜索整个树写法:
left = 递归函数(root->left); // 左
right = 递归函数(root->right); // 右
left与right的逻辑处理; // 中
上面两种写法的区别是:
搜索一条边时,我们遇到不符合条件的节点时就立马返回,然后换边搜索
搜索整个树时,我们使用一个变量去接收递归函数的返回值(是的,根据规则搜索整棵树时一般有返回值),然后在中节点处进行逻辑处理,并通过回溯返回到上一级递归
这也是为什么会"被迫"遍历整颗树的原因
言归正传
现在可以按照后序遍历顺序去写处理逻辑了
class Solution {
public:
//确定递归函数的输入和返回值
//因为需要通过返回值,在中节点位置判断父节点,且需要返回父节点值,故返回值应该是节点类型
TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
//确定终止条件
//当以下条件满足时,都要返回当前节点
if(root == NULL || root == q || root == p) return root;
//确定单层处理逻辑
//后序遍历
//左
TreeNode* left = lowestCommonAncestor(root->left, p, q);
//右
TreeNode* right = lowestCommonAncestor(root->right, p, q);
//中,在中节点位置处理左右的返回值,判断当前节点是否为最近公共父节点
//如果当前节点的左右子节点的返回值都不为空
//表明找到目标值,那么当前节点即为最近公共父节点
if(left != NULL && right != NULL) return root;
if(left == NULL && right != NULL){//左节点不为空右为空,说明当前节点不是公共父节点,把left再往上传(回溯)
return right;
}else if(left != NULL && right == NULL){//右节点不为空左为空,说明当前节点不是公共父节点,把right再往上传(回溯)
return left;
}else{// (left == NULL && right == NULL)
return NULL;//什么都没找到返回空
}
}
};
注意,这里我们是使用回溯过程中返回的值来判断公共父节点的
当前节点调用递归函数后,通过递归我们会寻找其下所有子节点中p、q存在的位置(题目说了必定存在,且不会是重复值)
当找到之后递归函数会通过回溯机制层层返回p、q
假如出现以下情况:(p、q不在同一分支)

这种情况的话,虽然不能马上找到最近公共父节点,但是通过层层递归并回溯p、q的值,总会在满足最近公共父节点的节点处触发条件
如果是代码分析中的情况1,那么返回一次就遇到了它们的最近公共父节点
如果是代码分析中的情况2,或者p、q距离比较远,那么就继续回溯返回呗,反正如果都找不到这个满足条件的公共父节点,那最后的最近公共父节点就是最开始调用递归的那个节点,也就是根节点
找二叉搜索树的最近公共祖先就简单多了↓
二叉搜索树的最近公共祖先
给定一个二叉搜索树, 找到该树中两个指定节点的最近公共祖先。
百度百科中最近公共祖先的定义为:“对于有根树 T 的两个结点 p、q,最近公共祖先表示为一个结点 x,满足 x 是 p、q 的祖先且 x 的深度尽可能大(一个节点也可以是它自己的祖先)。”
例如,给定如下二叉搜索树: root = [6,2,8,0,4,7,9,null,null,3,5]
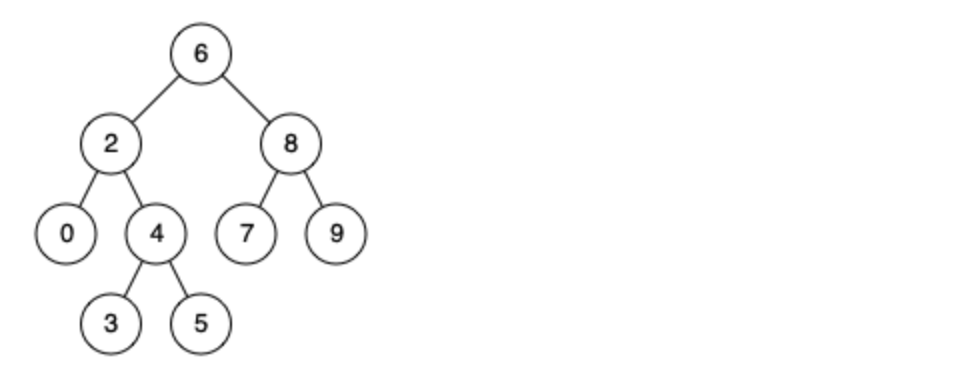
示例 1:
- 输入: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 8
- 输出: 6
- 解释: 节点 2 和节点 8 的最近公共祖先是 6。
示例 2:
- 输入: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 4
- 输出: 2
- 解释: 节点 2 和节点 4 的最近公共祖先是 2, 因为根据定义最近公共祖先节点可以为节点本身。
说明:
- 所有节点的值都是唯一的。
- p、q 为不同节点且均存在于给定的二叉搜索树中
思路
回想一下二叉搜索树的性质:
- 若它的左子树不空,则左子树上所有结点的值均小于它的根结点的值;
- 若它的右子树不空,则右子树上所有结点的值均大于它的根结点的值;
- 它的左、右子树也分别为二叉搜索树
利用这个性质可以进一步得知
若当前节点A是其左右子节点p、q的最近公共父节点
如果p、q在当前根节点A的左子树,那么节点A的值应该会满足:
A.val > p.val && A.val > q.val,节点A的值大于p、q范围,要往更小的那边去遍历(即节点A的左子树)
同理,如果p、q在当前根节点A的右子树,那么节点A的值应该会满足:
A.val < p.val && A.val < q.val,节点A的值小于于p、q范围,要往更大的那边去遍历(即节点A的右子树)
总结一下上述描述:在二叉搜索树中寻找最近公共父节点是靠判断当前节点(父节点)与目标值p、q之间的大小关系来实现的
什么意思?举个例子
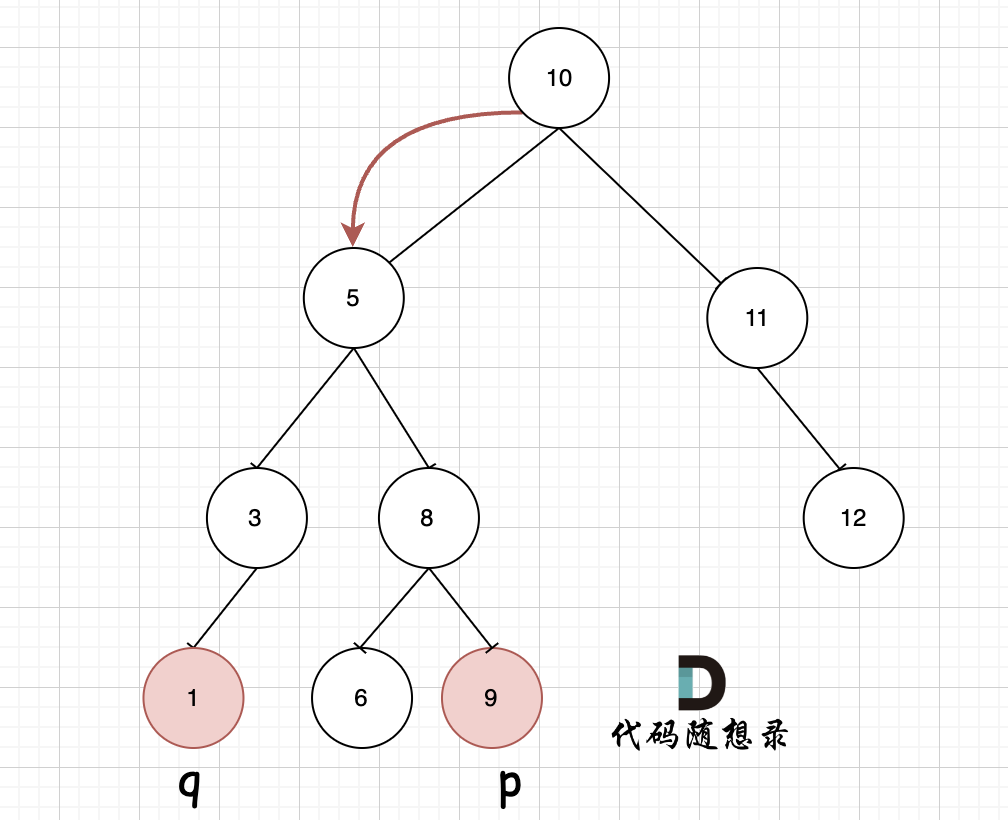
我们从 根节点10 开始遍历,此时的[p, q]是[1, 9](这里pq谁大谁小实际上是没有确定的),显然 根节点10 超出了[p, q]的范围,那么它就不可能是p、q的最近公共父节点,因此再往下遍历时,要走 根节点10 的左子树
(由于二叉搜索树的特性,其左子树里面的节点值均小于10,即有可能存在落在p、q区间内并且满足成为他们公共父节点的节点值)
遍历到 节点5 ,此时节点值已经落在[p, q]的范围内
如果继续向下遍历会出现以下结果:
- 向左,错过p;
- 向右,错过q;
因此,当我们在二叉搜索树里从上往下遍历时,如果遇到当前节点落在[p, q](或[q, p])里的情况,那么这个节点就是p、q的最近公共父节点
递归法
思路分析
1、确定递归函数的返回值和参数
这里我们不需要遍历整颗二叉树,且遇到满足条件的值就要返回,理论上来说应该是返回个bool就行了
但这里我们要找的是一个父节点,因此需要返回节点类型,传入参数与解题模板一致
class Solution {
public:
//确定递归函数的返回值和参数
TreeNode* traversal(TreeNode* root, TreeNode* p, TreeNode* q){
}
TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
}
};
2、确定终止条件
因为题目规定了p、q一定存在,那么递归一定会自行结束,所以其实有无终止条件都行
理论上,我们可以设置:当cur指向NULL后就终止
class Solution {
public:
//确定递归函数的返回值和参数
TreeNode* traversal(TreeNode* cur, TreeNode* p, TreeNode* q){
if(cur == NULL) return NULL;
}
TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
}
};
3、确定单层处理逻辑
从上往下遍历就行,顺序不限(这里没有中节点的处理逻辑,遍历顺序无所谓了)
当我们遍历到当前某个节点,其落在p、q的范围内,那么就结束遍历,返回该节点
class Solution {
public:
//确定递归函数的返回值和参数
TreeNode* traversal(TreeNode* cur, TreeNode* p, TreeNode* q){
if(cur == NULL) return NULL;//确定终止条件
//当前值大于p、q范围,往左子树遍历
if(cur->val > p->val && cur->val > q->val){
TreeNode* left = traversal(cur->left, p, q);
//如果往左子树不断递归搜索,有返回值说明找到,此时可以直接将结果返回
if(left != NULL) return left;
}
//当前值小于p、q范围,往右子树遍历
if(cur->val < p->val && cur->val < q->val){
TreeNode* left = traversal(cur->right, p, q);
//如果往右子树不断递归搜索,有返回值说明找到,此时可以直接将结果返回
if(right != NULL) return right;
}
//剩下的情况就是cur落到p、q范围内的情况,那么此时cur就是要找的节点,返回即可
return cur;
}
TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
}
};
完整代码
class Solution {
public:
//确定递归函数的返回值和参数
TreeNode* traversal(TreeNode* cur, TreeNode* p, TreeNode* q){
if(cur == NULL) return NULL;//确定终止条件
//当前值大于p、q范围,往左子树遍历
if(cur->val > p->val && cur->val > q->val){
TreeNode* left = traversal(cur->left, p, q);
//如果往左子树不断递归搜索,有返回值说明找到,此时可以直接将结果返回
if(left != NULL) return left;
}
//当前值小于p、q范围,往右子树遍历
if(cur->val < p->val && cur->val < q->val){
TreeNode* right = traversal(cur->right, p, q);
//如果往右子树不断递归搜索,有返回值说明找到,此时可以直接将结果返回
if(right != NULL) return right;
}
//剩下的情况就是cur落到p、q范围内的情况,那么此时cur就是要找的节点,返回即可
return cur;
}
TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
return traversal(root, p, q);
}
};
迭代法
本题的迭代解法最简单,推荐记忆
你二叉搜索树不是有顺序嘛,那我就直接从根节点开始一直往下遍历就好了
如果当前节点大于p、q范围,往左子树遍历
如果当前节点小于p、q范围,往右子树遍历
class Solution {
public:
TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
while(root){
if(root->val > q->val && root->val > p->val){
//当前节点大于p、q范围,往左子树遍历
root = root->left;
}else if(root->val < q->val && root->val < p->val){
//当前节点小于p、q范围,往右子树遍历
root = root->right;
}else{//在范围内
return root;
}
}
return NULL;
}
};
【LeetCode二叉树#16】二叉(搜索)树的最近公共祖先(递归后序遍历,巩固回溯机制)的更多相关文章
- Leetcode:230. 二叉搜索树中第K小的元素
Leetcode:230. 二叉搜索树中第K小的元素 Leetcode:230. 二叉搜索树中第K小的元素 思路: 利用BST的中序历遍的结果为其排序后的结果,我们可以利用其特性直接找到第k个中序遍历 ...
- leetcode 236. 二叉树的最近公共祖先LCA(后序遍历,回溯)
LCA(Least Common Ancestors),即最近公共祖先,是指在有根树中,找出某两个结点u和v最近的公共祖先. 题目描述 给定一个二叉树, 找到该树中两个指定节点的最近公共祖先. 百度百 ...
- 【LeetCode-面试算法经典-Java实现】【145-Binary Tree Postorder Traversal(二叉树非递归后序遍历)】
[145-Binary Tree Postorder Traversal(二叉树非递归后序遍历)] [LeetCode-面试算法经典-Java实现][全部题目文件夹索引] 原题 Given a bin ...
- 代码随想录算法训练营day20 | leetcode ● 654.最大二叉树 ● 617.合并二叉树 ● 700.二叉搜索树中的搜索 ● 98.验证二叉搜索树
LeetCode 654.最大二叉树 分析1.0 if(start == end) return节点索引 locateMaxNode(arr,start,end) new root = 最大索引对应节 ...
- 【LeetCode】230. 二叉搜索树中第K小的元素 Kth Smallest Element in a BST
作者: 负雪明烛 id: fuxuemingzhu 个人博客: http://fuxuemingzhu.cn/ 公众号:负雪明烛 本文关键词:算法题,刷题,Leetcode, 力扣,二叉搜索树,BST ...
- Java实现 LeetCode 450 删除二叉搜索树中的节点
450. 删除二叉搜索树中的节点 给定一个二叉搜索树的根节点 root 和一个值 key,删除二叉搜索树中的 key 对应的节点,并保证二叉搜索树的性质不变.返回二叉搜索树(有可能被更新)的根节点的引 ...
- 【LeetCode】230#二叉搜索树中第K小的元素
题目描述 给定一个二叉搜索树,编写一个函数 kthSmallest 来查找其中第 k 个最小的元素. 说明: 你可以假设 k 总是有效的,1 ≤ k ≤ 二叉搜索树元素个数. 示例 1: 输入: ro ...
- 剑指offer:二叉搜索树的第k个结点(中序遍历)
1. 题目描述 /* 给定一棵二叉搜索树,请找出其中的第k小的结点. 例如, (5,3,7,2,4,6,8) 中,按结点数值大小顺序第三小结点的值为4. */ 2. 思路 中序遍历二叉搜索树,第K个就 ...
- C++实现对树的创建和前中后序遍历
#include<iostream>#include<stdio.h> using namespace std; class BitNode{ public: char dat ...
- 代码随想录算法训练营day22 | leetcode 235. 二叉搜索树的最近公共祖先 ● 701.二叉搜索树中的插入操作 ● 450.删除二叉搜索树中的节点
LeetCode 235. 二叉搜索树的最近公共祖先 分析1.0 二叉搜索树根节点元素值大小介于子树之间,所以只要找到第一个介于他俩之间的节点就行 class Solution { public T ...
随机推荐
- 【转帖】Docker容器四种网络模式
https://blog.whsir.com/post-5268.html docker自身默认提供了四种网络模式:none.bridge.container.host.除了这四种网络模式外,还可以通 ...
- [转帖]整理常用的 vim 命令
vim 是一款功能强大的文本编辑器,它是Linux下常用的编辑器之一,对于熟练掌握了 vim 的人来说,用它编辑文件,方便又快捷,能极大的提高工作效率 vim 功能强大,对应的命令也非常的多,对于初学 ...
- [转帖]java -d 参数(系统属性) 和 环境变量
https://www.cnblogs.com/limeiyang/p/16565920.html 1. -d 参数说明 通过 java -h 查看可知: 注意:-D= : set a system ...
- Sysbench的简单学习-编译与安装
sysbench的简单学习-编译与安装 摘要 github上面获取一下最新版本 https://github.com/akopytov/sysbench 注意现在 2023.2.17 最新版是 sys ...
- zabbix 6.0 官方文档
Choose your platform ZABBIX VERSION 6.0 LTS 5.4 5.0 LTS 4.0 LTS OS DISTRIBUTION Red Hat Enterprise ...
- CCFLOW源码解读系列01-----发起流程
1.发起流程 发起流程时主要做了两件事:一是写入业务数据表,二是新建一条审批流程记录. 发起流程的方法 public static Int64 Node_CreateStartNodeWork(str ...
- clion运行单个c和c++文件(.c.cpp)
运行方法 在clion中安装插件:C/C++Single File Execution 在要执行的cpp文件中添加main函数 在cpp文件的编辑器界面中点右键会出现[Add executable f ...
- vim 从嫌弃到依赖(19)——替换
之前讨论了关于在vim中使用正则表达式的相关知识能方便的进行搜索,现在在之前的基础之上继续来讨论如何进行替换操作. substitute 简介 substitute 允许我们先查找一段文本并用新的文本 ...
- ChatGPT 对接微信公众号技术方案实现!
作者:小傅哥 博客:https://bugstack.cn 沉淀.分享.成长,让自己和他人都能有所收获! 9天假期写了8天代码和10篇文章,这个5.1过的很爽! 如假期前小傅哥的计划一样,这个假期开启 ...
- Windows 10 ISO原版镜像文件下载(2024年01月)
Windows 10 (business editions), version 22H2 (x64) - DVD (Chinese-Simplified) 链接:https://pan.baidu.c ...
